Теорема Піфагора(розробка для позакласної роботи)
РОЖИЩЕНСЬКА РАЙОННА ДЕРЖАВНА АДМІНІСТРІЦІЯ
ВІДДІЛ ОСВІТИ ТА МОЛОДІ
Рожищенський районний методичний кабінет
Загальноосвітня школа І-ІІ ступеня с.Вічині
Юлія Анатоліївна Мазелюк
Теорема Піфагора
(розробка для позакласної роботи)
2019
Мазелюк Юлія Анатоліївна, вчитель математики. «Теорема Піфагора» (розробка для позакласної роботи). – Вічині: загальноосвітня школа І-ІІ ступеня, 2019. – 27с.
Визначне місце при вивченні геометрії у 8 класі має тема «Теорема Пфагора».
В даній роботі сформульована теорема Піфагора; наведено 4 способи її доведення; розглянуто приклади розв’язування задач на застосування теореми Піфагора; згадані історичні відомості з біографії Піфагора
Видання розраховане для вчителів математики при викладанні геометрії у 8 класі та в позакласній роботі.
Рецензенти:
С. М. – методист з математико Рожищенського районного методичного кабінету
Михалюк М. А. – вчитель фізики та математики ЗОШ І-ІІ ст. с.Вічині
Схвалено методичною радою
Рожищенського районного методичного кабінету
(протокол № 3 від 14 лютого 2019 року)
ЗМІСТ
Вступ…….………………………………………………………………………….4
- Історична довідка …………………………………………………………5
2. Теорема Піфагора…………..………………………………………….….8
3.Приклади розв’язування задач на застосування теореми Піфагора……………………..……………………………………………….......10
4.Задачі практичного змісту…………………………………………...12
5. Завдання з фантазією на застосування теореми Піфагора………....16
6. Завдання для самостійного розв’язування…………………………..…23
Використана література………………………………….……………………..26
ВСТУП
Сучасний шкільний курс геометрії має великі розвиваючі можливості завдяки своїй цілісності й логічній строгості. Багатьом учням геометрія здається нелегкою і малозрозумілою, тому нерідко діти намагаються запам’ятати правила, не розуміючи їх, а це гальмує подальше розуміння нового матеріалу.
Здобуті учнями міцні знання тоді, коли вони є результатом свідомої самостійної роботи думки. Досить значним стимулом самовираження дітей у різних видах навчально-пізнавальної роботи є позакласна робота з геометрії. Ця робота пов’язана з чинною програмою і, водночас, дає змогу дитині виявити себе у нестандартних ситуаціях.
Однією із найважливіших тем в курсі геометрії, що заслуговує на пильну увагу, — є теорема Піфагора. Вона є основою розв'язування багатьох геометричних задач і базою вивчення теоретичного курсу надалі; містить багатий історичний матеріал. Теорема Піфагора — це основа евклідової геометрії, завдяки їй доводиться більшість теорем геометрії, тому її необхідно добре засвоїти.
-
 Історична довідка
Історична довідка
Піфагор жив у VI столітті до нашої ери. Він народився у Греції, на острові Самос у сім’ї золотих справ майстра Мнесарха. Можливості дати сину гарну освіту та виховання у Мнесарха були. Як і будь-який батько, Мнесарх мріяв, що син буде продовжувати його справу - ремесло золотих справ майстра. Життя вирішило інакше. Майбутній математик та філософ вже в дитинстві виявив велику здатність до наук. У свого першого вчителя Гермодамаса Піфагор отримав знання основ музики та живопису. Для покращення пам’яті Гермодамас примушував його вчити пісні з «Іліади» та «Одіссеї». Перший вчитель навчив Піфагора любити природу та вивчати її таємниці.
 Пройшло кілька років, і за порадою свого вчителя Піфагор вирішує продовжити навчання в Єгипті, у жерців. Потрапити до Єгипту у той час було дуже важко, тому що країну практично закрили для греків. За допомогою вчителя Піфагору вдається залишити острів Самос. Але до Єгипту далеко, і Піфагор поки що живе на острові Лесбос. Там відбувається знайомство Піфагора з філософом Ферекідом – другом Фалеса. У Ферекіда Піфагор навчається астрології, таємницям чисел, медицині та іншим обов’язковим, на той час, наукам. Піфагор прожив на Лесбосі кілька років. Звідти шлях Піфагора лежить у Мілет до відомого Фалеса, засновника першої в історії філософської школи.
Пройшло кілька років, і за порадою свого вчителя Піфагор вирішує продовжити навчання в Єгипті, у жерців. Потрапити до Єгипту у той час було дуже важко, тому що країну практично закрили для греків. За допомогою вчителя Піфагору вдається залишити острів Самос. Але до Єгипту далеко, і Піфагор поки що живе на острові Лесбос. Там відбувається знайомство Піфагора з філософом Ферекідом – другом Фалеса. У Ферекіда Піфагор навчається астрології, таємницям чисел, медицині та іншим обов’язковим, на той час, наукам. Піфагор прожив на Лесбосі кілька років. Звідти шлях Піфагора лежить у Мілет до відомого Фалеса, засновника першої в історії філософської школи.
Піфагор уважно слухає в Мілеті лекції Фалеса, якому на той час було вже 80 років, та його учня Анаксімандра, відомого географа й астронома. Багатьма важливими знаннями оволодів Піфагор за час свого навчання в Мілетській школі. Але Фалес теж радить йому поїхати до Єгипту, щоб продовжити навчання. І Піфагор відправляється у дорогу.
Перед Єгиптом він на деякий час зупиняється у Фінікії, де, за легендою, навчається у відомих сідонських жреців. Поки він живе в Фінікії, його друзі добилися того, щоб Полікрат – власник Самоса, не лише вибачає втікача, але навіть посилає йому рекомендаційного листа для Амазіса – фараона Єгипту. В Єгипті завдяки допозі Амазіса Піфагор знайомиться з мемфійськими жрецями. Йому вдається потрапити в єгипетські храми, куди чужоземців не пускали. Щоб прилучитися до таємниць єгипетських храмів, Піфагор приймає посвячення в сан жреця.
Навчання Піфагора в Єгипті сприяє тому, що він стає одним із найбільш освічених людей свого часу. Волею долі 12 років прожив Піфагор у Вавилоні, де прилучився до східної астрології та містики. І тільки в 60 років Піфагору вдалося повернутися на Батьківщину.
Після повернення додому Піфагор переселився до Південної Італії, яку тоді називали великою Грецією. Тут, на острові Сицилія в Кротоні, у нього народжується власна філософська школа.
Багато зробив вчений і для геометрії. Доведена Піфагором знаменита теорема носить його ім’я. Достатньо грунтовно дослідив Піфагор і математичні відношення, закладаючи тим самим основи теорії пропорцій.
Особливу увагу він приділяв числам та їх властивостям, пориваючись зрозуміти значення та природу речей. Мабуть, найпопулярнішою з усіх теорем є теорема Піфагора. Причинами такої популярності є простота, краса, значення. Справді, теорема Піфагора проста, але не очевидна. Це поєднання двох суперечностей і надає їй особливої привабливості. Окрім цього, теорема Піфагора має велике значення: вона використовується на кожному кроці, той факт, що існує близько 500 різних доказів цієї теореми доводить велику кількість її реальних реалізацій. Відкриття теореми Піфагором оточене ореолом
красивих легенд. Прокл, коментуючи останнє продовження першої книги “Начал” Евкліда, пише: “Якщо послухати тих, хто повторює давні легенди, то доводиться сказати, що ця теорема походить від Піфагора; розповідають, що він у честь цього відкриття приніс у жертву бика”.
Дехто розповідає, що він приніс у жертву не одного бика, а цілу сотню.
На цю тему німецький поет Альберт фон Шаміссо написав вірш:
Про теорему Піфагора
Суть істини проста: вона — дороговказ,
Що сяє для людей, одвічна і сувора,
Тому, як в давнину, вражає нині нас
Беззаперечна теорема Піфагора.
За дотик мудрості уславлених богів,
Ковток із джерела незвіданого смаку,
Олімпу Піфагор тоді осанну звів
І сто биків заклав жертовних на подяку.
Відтоді всі бики, як чують серед нив,
Що людство прагне знов за обрії духовні,
Збентежено ревуть, хоча і ясла повні,
Такий в них Піфагор навіки жах вселив.
Не зборе бик того, що істина зборола
Тому вони й ревуть, схиливши очі долу.
Сьогодні теорема Піфагора виявлена у різних часткових задачах та кресленнях: і в єгипетському трикутнику в папірусі часів фараона Аменемхета І (біля 2000р. до н. е.), і у вавилонських клинописних табличках епохи царя Хаммурапі (XVIII ст. до н. е.), і в давньоіндійському трактаті VII-V ст. до н. е. “Сульва сутра”. У найдавнішому китайському трактаті “Чжоубі суань цзинь” час створення якого точно не відомо, стверджується, що в XII ст. до н. е. Китайці знали властивості єгипетського трикутника, а до VI ст. до н. е. – й загальний вигляд теореми. Не дивлячись на це, ім’я Піфагора щільно злилося з теоремою Піфагора. Сьогодні прийнято вважати, що Піфагор першим довів теорему, яка носить його ім’я. На жаль, його доказ не дійшов до нашого часу.
2. Теорема Піфагора
Теорема Піфагора. У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів.
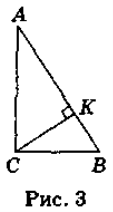 Доведення 1. Доведемо теорему Піфагора, застосовуючи подібність трикутників.
Доведення 1. Доведемо теорему Піфагора, застосовуючи подібність трикутників.
Доведення
∆АСВ ![]() ∆СКВ (рис. 3), оскільки вони прямокутні і
∆СКВ (рис. 3), оскільки вони прямокутні і ![]() B — спільний, тоді
B — спільний, тоді
![]() ,
,
звідси
ВС2 = АВ · ВК
(або відразу можна використати той факт, що катет прямокутного трикутника є середнім пропорційним між гіпотенузою та проекцією цього катета на гіпотенузу). Аналогічно ∆АСВ ![]() ∆АКС, тоді
∆АКС, тоді
![]() ,
,
звідси
АС2= АК · АВ.
Отже, АС2 + ВС2 = АВ · ВК + АК · АВ = АВ(ВК + АК) = АВ · АВ = АВ2,
що й треба було довести.
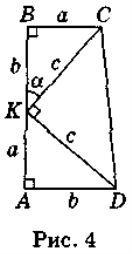 Доведення 2. Доведемо теорему, застосовуючи формули площ прямокутного трикутника, трапеції.
Доведення 2. Доведемо теорему, застосовуючи формули площ прямокутного трикутника, трапеції.
Доведення
Нехай ![]() ВКС = α (рис. 4). Оскільки ∆КВС = ∆DAK, то і
ВКС = α (рис. 4). Оскільки ∆КВС = ∆DAK, то і ![]() ADK = α.
ADK = α.
Отже, ![]() AKD = 90° - α, тому
AKD = 90° - α, тому
![]() CКD = 180° - α - (90°- α) = 90°.
CКD = 180° - α - (90°- α) = 90°.
![]() .
.
SABCD = S∆KBC + S∆DAK + S∆CKD = ![]() а · b +
а · b + ![]() a · b +
a · b + ![]() c2 = ab +
c2 = ab + ![]() c2.
c2.
Отже, ![]() ;
;
(a + b)2 = 2ab + c2; a2 + 2ab + b2 = 2ab + c2;
звідси
а2 + b2 = с2.
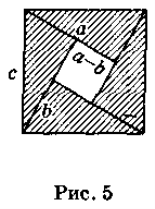 Доведення 3. Розглянемо індійське доведення з наукової точки зору. Для цього вам необхідно пригадати формули площі квадрата й прямокутного трикутника (рис. 5). Площа всіх чотирьох прямокутних трикутників:
Доведення 3. Розглянемо індійське доведення з наукової точки зору. Для цього вам необхідно пригадати формули площі квадрата й прямокутного трикутника (рис. 5). Площа всіх чотирьох прямокутних трикутників:
4S∆ = 4 ·![]() а · b = 2аb.
а · b = 2аb.
Площа більшого квадрата:
S□ = c2.
Площа меншого квадрата:
S1 = (a – b)2.
Тоді c2 – 2ab = (a – b)2;
c2 – 2ab = a2 – 2ab + b2;
с2 = а2 + b2.
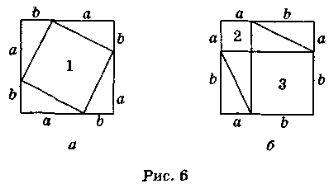 Доведення 4. Розріжемо квадрат зі стороною (а + b) двома способами (рис. 6). В обох випадках вийшло чотири прямокутних трикутники з катетами а і b, тому площа квадрата 1 дорівнює сумі площ квадратів 2 і 3. Але квадрат 1 побудований на гіпотенузі прямокутного трикутника з катетами а і b, а квадрати 2 і 3 побудовані на його катетах. Отже,
Доведення 4. Розріжемо квадрат зі стороною (а + b) двома способами (рис. 6). В обох випадках вийшло чотири прямокутних трикутники з катетами а і b, тому площа квадрата 1 дорівнює сумі площ квадратів 2 і 3. Але квадрат 1 побудований на гіпотенузі прямокутного трикутника з катетами а і b, а квадрати 2 і 3 побудовані на його катетах. Отже,
с2 = а2 + b2.
Теорему доведено.
3. Приклади розв’язування задач на застосування теореми Піфагора
1. Основа рівнобедреного трикутника 16см, а висота, проведена до основи, дорівнює 6см. Знайдіть бічну сторону трикутника.
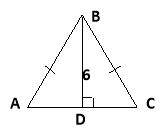
Дано: АС – основа, АС = 16см,
ВD – висота, ВD = 6см.
Знайти: АВ.
Розв’язання:
∆АВС – рівнобедрений, ВD – висота.
За властивістю висоти рівнобедреного трикутника ВD – медіана,
АD = DС = 8см.
∆АВD – прямокутний, за теоремою Піфагора:
![]()
Відповідь: 10 см.
2. Діагональ прямокутника дорівнює 10см, а одна з його сторін 8см. Знайдіть периметр прямокутника.
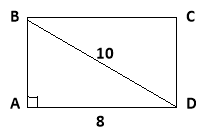 Дано: АВСD – прямокутник, ВD – діагональ,
Дано: АВСD – прямокутник, ВD – діагональ,
ВD = 10см, АD= 8 см.
Знайти: Р.
Розв’язання:
P= (АВ +ВС)× 2
АВD – прямокутний трикутник, за теоремою Піфагора:
![]() ;
; ![]() ;
;
![]()
Р = (6+8)× 2 = 28(см).
Відповідь: 28см.
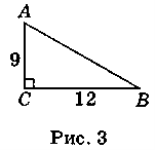
3.Ми з вами в літаку. Він перебуває на висоті 9 км,. На землі ми подолали відстань 12 км. Який шлях подолав літак у повітрі з моменту зльоту?
 Дано: ∆ACB,
Дано: ∆ACB, ![]() C = 90°, АС = 9 км; ВС = 12 км.
C = 90°, АС = 9 км; ВС = 12 км.
Знайти: АВ.
Розв’язання
Оскільки за умовою трикутник ABC (рис. 3) — прямокутний, то за теоремою Піфагора АВ2 = ВС2 + АС2; АВ2 = 92 + 122; АВ2 = 81 + 144 = 225; АВ = = 15 км.
Відповідь: літак подолав шлях, що дорівнює 15 км.
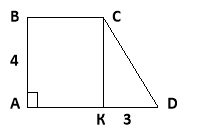
4. У прямокутній трапеції АВСD з основами АD і ВС, кут А – прямий, АВ = 4дм. З вершини С до основи АD проведений перпендикуляр СК, КD = 3дм. Знайдіть СD.
 Дано: АВСD – трапеция,
Дано: АВСD – трапеция, ![]()
![]() , АВ = 4 дм.
, АВ = 4 дм.
СК ![]() АD , КD = 3 дм.
АD , КD = 3 дм.
Знайти: СD.
Розв’язання:
Оскільки АВСD трапеція: АD![]() ВС, АВ
ВС, АВ![]() СК,
СК,
АВ = СК = 4дм.
Розглянемо ∆СDК, ![]()
За теоремою Піфагора: ![]() ;
; ![]() ;
;
![]() .
.
Відповідь: 5дм.
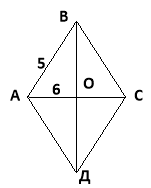
5. Сторона ромба дорівнює 5см, а його менша діагональ 6см. Знайдіть велику діагональ ромба.
Розв’язання:
 Ми знаємо, що за властивістю діагоналей ромба АС
Ми знаємо, що за властивістю діагоналей ромба АС![]() ВD і АО = ОС = 3см.
ВD і АО = ОС = 3см.
Отже ∆АОВ – прямокутний. За теоремою Піфагора:
АВ²=АО ²+ ВО²,
![]() (см), ВD = 2ВО = 8 (см).
(см), ВD = 2ВО = 8 (см).
Відповідь: 8см.
4.Задачі практичного змісту
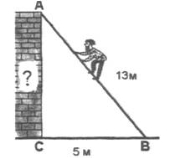
- Знайти висоту будівлі (рис. 1).
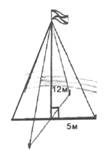
- Вертикальна щогла підтримується чотирма канатами, прикріпленими до неї на відстані 12 м від землі і на відстані 5 м від основи щогли. Скільки метрів мотузки потрібно, якщо на вузли витратили 10 м (рис. 2)?
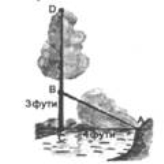
- Задача індійського математика XII ст. Бхаскари.
На березі річки тополя росла,
Та вітру порив її стовбур зламав.
Тополя упала, і стовбур її
Кут прямий з течією річки утворив.
Пам'ятайте, у тому місці ріка
4 фути була шириною.
Верхівка схилилась до краю,
Залишивши 3 фути всього над водою.
Прошу тепер швидше скажіть мені ви:
Тополя якої була висоти? (1фут = 0,3м.)
-
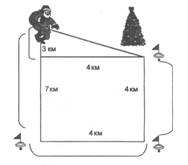
 Дід Мороз пройшов 7 км на південь, потім 4 км на схід і стільки само на північ. На яку відстань відійшов Дід Мороз від початкової точки?
Дід Мороз пройшов 7 км на південь, потім 4 км на схід і стільки само на північ. На яку відстань відійшов Дід Мороз від початкової точки?
![]()
![]()
![]()
![]()
-
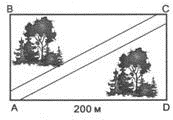
 Парк має форму прямокутника. Довжина однієї з його сторін дорівнює 200 м, а площа — 72 000 м2. Яка довжина головної алеї парку, що проходить по його діагоналі (рис. 5).
Парк має форму прямокутника. Довжина однієї з його сторін дорівнює 200 м, а площа — 72 000 м2. Яка довжина головної алеї парку, що проходить по його діагоналі (рис. 5).
-
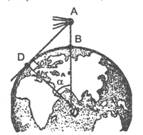
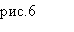 Космонавт під час польоту знаходиться на відстані 327 км над землею. На якій відстані від корабля знаходились у цей час найбільш віддалені від нього видимі ділянки поверхні Землі (рис. 6)? (Радіус Землі ≈ 6400 км.)
Космонавт під час польоту знаходиться на відстані 327 км над землею. На якій відстані від корабля знаходились у цей час найбільш віддалені від нього видимі ділянки поверхні Землі (рис. 6)? (Радіус Землі ≈ 6400 км.)
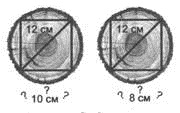
7. Діаметр колоди дорівнює 12 см. Чи можна з цієї колоди витесати квадратний брус із ребром: а) 10 см; б) 8 см?(рис.7)
8. Задача Л. Пізанського (XII—XIII ст.).
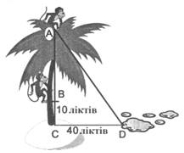
Дві вежі, одна з яких заввишки 40 футів, а друга — 30 футів, розташовані на відстані 50 футів одна від одної. До криниці, що була між ними, одночасно з кожної вежі злетіли пташки. Рухаючись з однаковою швидкістю, вони прилетіли до криниці одночасно. Знайти відстань від криниці до найближчої вежі (у футах). (рис.8)
9. («Стрибок мавпи»).
На дереві сиділи дві мавпочки: одна— на самій верхівці дерева, інша — на висоті 10 ліктів від землі. Другій мавпочці захотілося напитися води із джерела, що розміщене на відстані 40 ліктів від дерева. Вона злізла з дерева і пострибала до води. У той самий час перша зістрибнула з дерева і потрапила до того самого джерела. Обидві мавпочки подолали однакову відстань. З якої висоти стрибнула друга мавпочка (рис. 9)?
10.«Зламаний бамбук.»
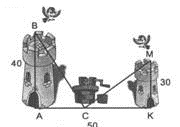
 Бамбук, що має 40 ліктів у висоту, було зламано вітром. Його верхівка торкнулася землі за 20 ліктів від основи стовбура. Скажи, о мудрий математик, на якій відстані від землі було зламано бамбук?
Бамбук, що має 40 ліктів у висоту, було зламано вітром. Його верхівка торкнулася землі за 20 ліктів від основи стовбура. Скажи, о мудрий математик, на якій відстані від землі було зламано бамбук?
![]()
![]()
![]()
Розв’язок задач практичного змісту
-
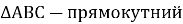 . За теоремою Піфагора:
. За теоремою Піфагора:
![]()
Відповідь: 12 м.
Відповідь: 62 м.
![]()
Відповідь: 2,4 м.
Відповідь: 5 км.
-
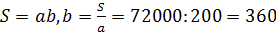 Запишемо формулу для знаходження площі прямокутника:
Запишемо формулу для знаходження площі прямокутника:
Використавши теорему Піфагора отримаємо:
![]() м.
м.
Відповідь: 411,83 м.
![]() , тоді за теоремою Піфагора:
, тоді за теоремою Піфагора:
![]()
Відповідь: 2071,84 км.
-
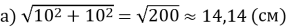 .
.
б)![]() .
.
Відповідь: а) ні; б) так.
![]()
Запишемо теорему Піфагора, отримаємо рівняння:
![]()
![]()
![]()
Отже, АС=18 футів, СК=50-18=32 (фути),
АС=18∙0,3=5,4 (м).
Відповідь: 18 футів (5,4 м).
- Маємо: ВС+CD=50 (лікт.) – це відстань, яку подолала друга мавпочка, AD=50 ліктів.
За теоремою Піфагора маємо:
![]() .
.
Відповідь: 30 ліктів.
10.
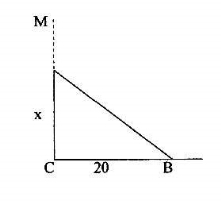 МА=АВ
МА=АВ
АС+АВ=40;
Нехай АС=х; АВ=40-х
![]() - за т.Піфагора
- за т.Піфагора
![]()
Отримаємо рівняння:
![]()
![]()
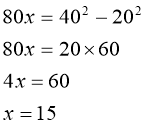
Відповідь: 15 ліктів.
5. Завдання з фантазією на застосування теореми Піфагора
Ви думаєте, що теорема Піфагора - це зовсім нескладно? Ну, загалом, так. Але цікаві завдання все ж іноді можна зустріти. В основному ми зіткнемося тут з відносинами і порівнянням чисел.
1.Один з катетів прямокутного трикутника на 10 більше іншого і на 10 менше гіпотенузи. Знайдіть гіпотенузу цього трикутника.
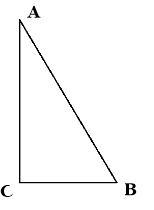 Розв’язання: Запишемо для цього трикутника теорему Піфагора. Для цього позначимо катети
Розв’язання: Запишемо для цього трикутника теорему Піфагора. Для цього позначимо катети ![]() . А гіпотенузу
. А гіпотенузу ![]() . Тоді
. Тоді
![]()
![]()
![]()
Звідки ![]() . Тоді гіпотенуза на 10 більше – 50.
. Тоді гіпотенуза на 10 більше – 50.
Відповідь: 50.
2.У трикутнику ABC кут BAC прямий, довжини сторін AB і BC дорівнюють відповідно 1 і 3. Точка K ділить сторону AC в відношенні 7: 1, рахуючи від точки A. Що більше: довжина AC або довжина BK?
Розв’язання:
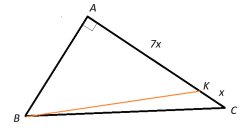
Щоб знайти ![]() , яка є бісектрисою в трикутнику
, яка є бісектрисою в трикутнику ![]() , Потрібно знати довжину катета
, Потрібно знати довжину катета ![]() . Знайдемо його:
. Знайдемо його:
![]()
Тепер для трикутника ![]() складемо теорему Піфагора
складемо теорему Піфагора
![]()
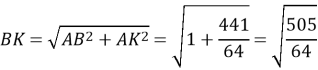
Залишилося порівняти числа ![]() i 3. Запишимо останнє як
i 3. Запишимо останнє як
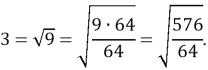
Відповідь: довжина AC більша.
3.У прямокутнику ABCD довжини відрізків AB і BD рівні відповідно 2 і . Точка M ділить відрізок CD в співвідношенні 1: 2, рахуючи від точки C, K - середина AD. Що більше: довжина BK або довжина AM?
Розв’язання:
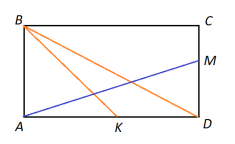 Спочатку знайдемо
Спочатку знайдемо ![]() .
.
![]()
![]()
![]()
![]()
![]()
Розглянемо трикутник ![]() , де
, де ![]() гіпотенуза
гіпотенуза
![]()
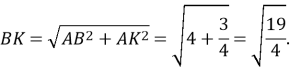
Знайдемо тепер ![]()
![]()
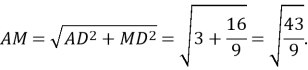
Порівняємо дроби ![]() і
і ![]() . Звівши до спільного знаменника отримаємо
. Звівши до спільного знаменника отримаємо
![]()
![]()
Відповідь: довжина ![]() більша за довжину
більша за довжину ![]() .
.
\
4.У трикутнику ABC кут BAC прямий, довжини сторін AB і AC дорівнюють відповідно 5 і 6. Точка K ділить сторону AC в відношенні 3: 1, рахуючи від точки A, AH - висота трикутника ABC. Що більше: 2 або відношення довжини BK до довжини AH?
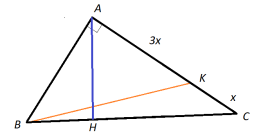 Розв’язання: Щоб знайти висоту AH трикутника, знайдемо його подвійну площу:
Розв’язання: Щоб знайти висоту AH трикутника, знайдемо його подвійну площу:
![]()
![]()
![]() знайдемо за теоремою Піфагора:
знайдемо за теоремою Піфагора:
![]()
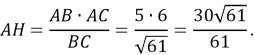
Знайдемо![]() :
: ![]()
Звідси маємо:
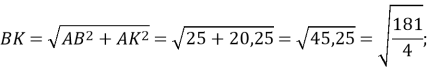
Складемо відношення :
![]()
Порівняємо ![]() i 2
i 2
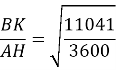
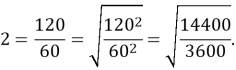
Відповідь: ![]() .
.
5.У трикутник ABC довжина підстави AC дорівнює 2 , довжина бокової сторони дорівнює 8. Точка K ділить висоту BD трикутника відносно 2: 3, рахуючи від точки B. Що більше: довжина CK або довжина AC?
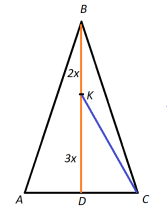 Розв’язання: Знайдемо висоту
Розв’язання: Знайдемо висоту ![]()
![]()
Знайдемо ![]()
![]()
За теоремою Піфагора знайдемо ![]() :
:
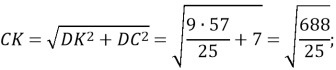
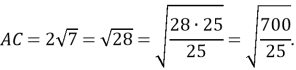
Відповідь: ![]() .
.
6.Знайдіть радіуси вписаного та невписаного кіл трикутника зі сторонами 3, 4, 5.
Розв’язання: Данний трикутник підлягає теоремі Піфагора, він парямокутний. Його гіпотенуза AB=5. Нехай катети ВС=3, АС=4.
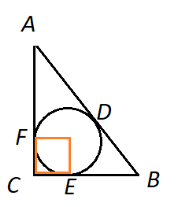 Спочатку розглянемо вписане коло.
Спочатку розглянемо вписане коло.
Нехай D, E, F – точки дотику кола до трикутника.
Тоді за теоремою про дотичні, проведені із однієї точки CF=CE. Довжини цих відрізків рівні радіусу ![]() . Тоді
. Тоді
![]()
![]()
![]()
![]()
Звідки
![]()
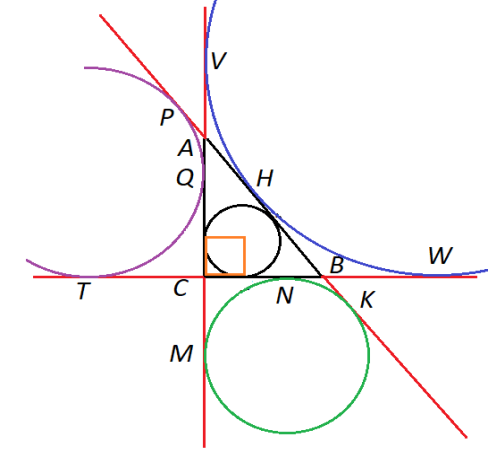
За теоремою про відрізки дотичних, проведених з однієї точки, ![]() . Але
. Але ![]() Тоді
Тоді ![]() знову ж за властивістю дотичних. Тоді
знову ж за властивістю дотичних. Тоді ![]() то
то
![]()
Розглянемо невписане коло, яке знаходиться ліворуч.
![]()
Але ![]() . Тоді
. Тоді ![]()
![]() за властивістю дотичних.
за властивістю дотичних.
Тоді ![]()
Так як ![]() , то
, то
![]()
Розглоянемо найбільше невписане коло(знаходиться правіше).
![]()
![]()
![]()
![]()
![]()
Відповідь: ![]()
7.З однієї точки проведені до даної прямої перпендикуляр і дві похилі. Знайдіть довжину перпендикуляра, якщо похилі рівні 41 і 50, а їх проекції на дану пряму відносяться як 3: 10.
Розв’язання: За теоремою Піфагора:
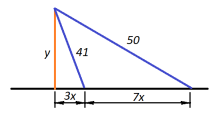
![]()
![]()
![]()
![]()
![]()
звідси випливає ![]()
Відповідь: 40.
8. У прямокутному трикутнику точка дотику вписаного кола ділить гіпотенузу на відрізки, рівні 5 і 12. Знайдіть катети трикутника.
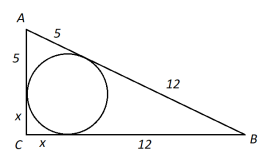 Розв’язання: За властивостями дотичних, проведених до кола з однієї точки, маємо:
Розв’язання: За властивостями дотичних, проведених до кола з однієї точки, маємо: ![]()
![]() Тоді
Тоді
![]()
![]()
![]()
Використавши теорему Вієта отримаємо: ![]() За умовою задачі підходить тільки додатній корінь.
За умовою задачі підходить тільки додатній корінь.
Отже, катети тоді рівні 8 і 15.
Відповідь: 8 і 15.
9.У прямокутному трикутнику медіани, проведені з вершин гострих кутів, рівні ![]() і
і ![]() . Знайдіть гіпотенузу трикутника.
. Знайдіть гіпотенузу трикутника.
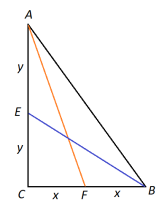 Розв’язання: Запишемо теорему Піфагора для трикутників
Розв’язання: Запишемо теорему Піфагора для трикутників ![]() . Нехай
. Нехай ![]() тоді
тоді
![]()
Якщо ![]() , то
, то
![]()
Перше рівняння помножимо на 4, щоб зрівняти коефіцієнти:
![]()
Віднімемо від першого рівняння друге:
![]()
![]()
Звідси випливає ![]() катети трикутника 6 і 8, а значить гіпотенуза 10.
катети трикутника 6 і 8, а значить гіпотенуза 10.
Відповідь: 10.
6. Завдання для самостійного розв’язування
1) Катети прямокутного трикутника 5 см і 12 см. Знайдіть гіпотенузу.
2) Гіпотенуза трикутника 5 см, а один із катетів дорівнює 3 см. Знайдіть другий катет.
3)У прямокутному трикутнику з катетами а і b та гіпотенузою с знайдіть с, якщо ![]()
4) Катети прямокутного трикутника відносяться як 3: 4, а гіпотенуза дорівнює 15 см. Знайдіть периметр трикутника.
5) Периметр квадрата дорівнює 4 см. Знайдіть діагональ квадрата.
6) Визначте вид трикутника ABC, якщо: 1) АС = 5, ВС = 6 , АС = 7;
2) АС = 4, ВС =![]() , AC = 6.
, AC = 6.
7) У прямокутнику знайдіть периметр, якщо діагональ дорівнює 10 см, а одна зі сторін — 6 см.
8) Основа рівнобедреного трикутника дорівнює 16 см.Знайдіть периметр трикутника, якщо його бісектриса, проведена до основи, дорівнює 6 см.
9) У прямокутному трикутнику знайдіть невідомі сторони, якщо:
а) катети відносяться як 3 : 4. а гіпотенуза дорівнює 45 см;
б) різниця між гіпотенузою і катетом дорівнює 1 см, а другий катет дорівнює 5 см;
в) висота, проведена до гіпотенузи, дорівнює 12 см, а проекція одного з катетів на гіпотенузу має довжину 16 см.
10) Основи рівнобедреної трапеції дорівнюють 8 см і 18 см, а висота 12 см. Знайдіть периметр трапеції. Чи можна вписати в неї коло?
11) Дві більші сторони прямокутного трикутника дорівнюють 65 см і 63 см. Знайдіть третю сторону.
12)Периметр рівнобедреного трикутника дорівнює 36 см, а бічна сторона — 13 см. Знайдіть медіану трикутника, проведену до основи.
13) У прямокутному трикутнику знайдіть невідомі сторони, якщо:
а) катет і гіпотенуза відносяться як 12 : 13, а другий катет дорівнює 10см;
б) катет більший за свою проекцію на гіпотенузу на 8 см, а висота, проведена до гіпотенузи, дорівнює 24 см.
14) Основи прямокутної трапеції дорівнюють 21 см і 28 см, а більша бічна сторона — 25 см. Знайдіть периметр трапеції. Чи можна вписати в неї коло?
15) Медіана прямокутного трикутника, проведена до гіпотенузи, дорівнює 6,5 см. Знайдіть трикутники, якщо один із катетів має довжину 5 см.
16)Знайдіть радіус кола, описаного навколо прямокутного трикутника з катетами 8 дм і 15 дм.
17)Діагоналі паралелограма мають довжину 6 см і 8 см, а одна зі сторін — 5 см. Що можна сказати про цей паралелограм?
18) Відомо, що довжина сторін паралелограма 5 см і 12 см, а одна з діагоналей має довжину 13 см. Що можна сказати про цей паралелограм?
19)Визначте, чи є в трикутнику прямий кут, якщо його сторони: а) 40 см, 41 см, 9см; б) 25 см, 24 см, 27 см.
20)У ΔSTO ST2 + ТО2 = SO2. Яка градусна міра найбільшого кута ΔSTO?
21)Знайти гіпотенузу рівнобедреного прямокутного трикутника, якщо його катет дорівнює: а)1 см; б)![]() .
.
22) Знайти катети рівнобедреного прямокутного трикутника, якщо його гіпотенуза дорівнює: а)![]() ; б)8см.
; б)8см.
23) Знайти сторони ромба, якщо його діагоналі дорівнюють: а)6 см і 8 см; б)18см і 24см.
24)Основи рівнобічної трапеції дорівнюють 6 і 18, а висота – 16 см. Знайти площу і діагональ трапеції.
25) Висота ромба, проведена з вершини тупого кута, ділить сторону на відрізки 6см і 4см , рахуючи від вершини гострого кута. Знайти радіус кола вписаного у ромб.
26) У прямокутному трикутнику медіана і висота, проведені із вершини прямого кута дорівнюють 17см і 15см. Знайти периметр трикутника.
27)У прямокутному трикутнику один катет дорівнює 60 см, а сума гіпотенузи і другого катета на 12 см більша. Знайти гіпотенузу і другий катет.
28) Висота і медіана, проведені до сторони с=42см, дорівнюють відповідно 12см і 13см. Знайти дві інші сторони.
29) Знайти висоти трикутника, якщо його сторони дорівнюють: 1) 10см, 10см, 12см; 2) 7см, 15см, 20 см.
30) Знайти висоту рівностороннього трикутика зі стороною ![]() .
.
31) Основа рівнобедреного трикутника на 2см більша за бічну сторону. Знайдіть сторони трикутника, якщо висота, проведена до основи – 8см.
32) Периметр рівнобедреного трикутника дорівнює 90 см, а висота, проведена до основи – 15см. Знайдіть сторони трикутника.
33) Точка дотику кола, вписаного в прямокутний трикутник, поділяє один із його катетів на відрізки 2 см і 6 см, рахуючи від вершини прямого кута. Знайдіть сторони трикутника.
34) Знайти сторони паралелограма, діагоналі якого дорівнюють 16см і 20см і одна з них перпендикулярна до сторони.
35) Знайти периметр прямокутного трикутника, якщо бісектриса прямого кута поділяє гіпотенузу на відрізки завдовжки 30 см і 40см.
36) Основи рівнобічної трапеції дорівнюють 12 см і 20см, а діагональ є бісектрисою її тупого кута. Знайдіть цю діагональ.
37) У колі по різні боки від його центра проведено дві паралельні хорди завдовжки 16см і 32см, відстань між хордами – 16см. Знайдіть радіус кола.
38) Радіус кола, вписаного в рівнобедрений трикутник, дорівнює 12 см, а відстань від вершини рівнобедреного трикутника до центра кола – 20см. Знайти периметр даного трикутника.
39) Точка дотику кола, вписаного в прямокутну трапецію, поділяє її більшу основу на відрізки 20см і 25см, рахуючи від вершини прямого кута. Обчисліть периметр трапеції.
40) Катети прямокутного трикутника дорівнюють 18см і 24 см. Знайти бісектрису трикутника, проведену з вершини меншого гострого кута.
ВИКОРИСТАНА ЛІТЕРАТУРА
- Бевз Г. П. Геометрія: Підручник для 8 кл. середніх загальноосвітніх закладів / Г.П. Бевз, В. Г. Бевз, Н. Г. Владімірова. – К.: Вежа, 2008. – 256 с.
- Бурда М. І. Геометрія: Підручник для 8 кл. загальноосвітніх навчальних закладів / М. І. Бурда, Н. А. Тарасенкова. – К.: Зодіак –ЕКО, 2008.- 240 С.
- Мерзляк А. Г. Геометрія. 8 кл.: Підручник для 8 кл. загальноосвітніх навчальних закладів / А. Г. Мерзляк, В. Б. Полонський, М. С. Якір. – К.: Гімназія, 2009. – 208 с.
- Мерзляк А. Г. Геометрія. 8 кл.: збірник задач і контрольних робіт / А. Г. Мерзляк, В. Б. Полонський, Ю. М. Рабінович, М. С. Якір. – Х.: Гімназія, 2011. – 112с.
- Погорєлов О. В. Геометрія 7 – 9 / О.В. Погорєлов. – К.:Освіта, 2001.
- Роганін О.М. Математика. Усе про ЗНО-2010 + тренувальні вправи / О. М. Роганін. – Х.: ФОП Співак Т.К., 2009. – 208 с.
- Чижова О.І. Самостійні роботи з математики. 5-9 клас / О. І. Чижкова. – Х.: Видавнича група «Основа», 2005. – 288 с.
- Шкільне життя
https://www.schoollife.org.ua/
1


про публікацію авторської розробки
Додати розробку
