Міністерство освіти і науки України

Управління освіти і науки Тернопільської облдержадміністрації

Тернопільське обласне комунальне територіальне відділення МАН України

 

 

 

Відділення: математики

Секція: математика

 

 

 

 

«Стародавні методи доведення теореми Піфагора»

 

 

 

 

 

 

Роботу підготував:

Учень _ класу

Шумського ліцею

___________________

Керівник:

Кравчук Володимир Анатолійович

вчитель математики та інформатики

Шумського ліцею

ТЕЗИ

Назва роботи: «Стародавні методи доведення теореми Піфагора»

Автор: ________________, __ клас, м. Шумськ

Назва загальноосвітнього навчального закладу: Шумський ліцей

Науковий керівник: вчитель математики Шумського ліцею, вчитель І категорії – Кравчук Володимир Анатолійович

Теоремою Піфагора займалося багато математиків протягом багатьох століть. Її приписують Піфагору, хоча ця теорема, або її частинні випадки були відомі в Єгипті, Вавилоні, Китаї. На сьогодні відомі різні підходи до доведення відомої теореми, але сутність її не змінюється.

В результаті дослідження було виявлено, що теорема Піфагора була відома ще задовго до нього і існує близько 500 доведень цієї теореми. Одне з найдавніших походить з Індії, а відкриття та розуміння теореми проходило в декілька етапів. На думку Плутарха та Цицерона саме Піфагор зробив завершальний крок в її формулюванні та доведенні  За допомогою теореми Піфагора можна довести ряд геометричних тверджень, розв’язати прикладні задачі, задачі практичного характеру.

 

ЗМІСТ

Зміст.                                                  3

Вступ.                                                               4

Розділ 1. Біографія Піфагора.                                   5

Розділ 2. Неалгебраїчні доведення теореми.                         7

2.1. Найпростіше доведення.                             7

2.2. Давнє китайське доведення.                              7

2.3. Древнє індійське доведення.                             8

2.4. Доведення Евкліда.                                   9

Розділ 3. Алгебраїчні доведення теореми.                          10

3.1. Передумова.                                     10

3.2. Алгебраїчне доведення теореми.                           10

3.3. Доведення на основі подібності трикутників.                  11

3.4. Доведення на основі поняття косинуса кута.                   11

Розділ 4. Застосування теореми Піфагора.                          13

Висновки.                                               16

Список використаної літератури.                                 18

Додатки.                                                 19

Додаток А.                                            19

Додаток Б.                                         20

Додаток В .                                           21

Додаток Г .                                           22

Додаток Д .                                           23

Додаток Е .                                           23

Додаток Є .                                           24

ВСТУП

Важко знайти людину, в якої ім’я Піфагора не асоціювалось би з теоремою Піфагора. Навіть ті, які давно не мають справи з математикою, зберігають спогади про «Піфагорові штани» - квадрат на гіпотенузі рівновеликий двом квадратам на катетах. Причина такої знаменитості теореми триєдина: це простота – красота – значимість.

Дійсно, теорема Піфагора проста, але не очевидна. Саме завдання теореми робить її красивою. Проте теорема Піфагора має велике значення: вона застосовується в геометрії, практично на кожному кроці. Так як існує біля 500 різних доведень цієї теореми (алгебраїчних, геометричних, механічних), саме це говорить про гігантське число її застосування.

Актуальність теми. Теоремою Піфагора займалося багато математиків протягом багатьох століть. Її приписують Піфагору, хоча ця теорема або її частинні випадки були відомі в Єгипті, Вавилоні, Китаї. На сьогодні відомі різні підходи до доведення відомої теореми, але сутність її не змінюється. Велике значення має теорема для розв’язування геометричних задач та задач прикладного характеру. Мені стало цікаво, чи багато існує різних підходів до доведення теореми Піфагора.

Предметом мого дослідження  стали доведення різними математиками великої теореми.

Мета наукової роботи: поглибити знання про різні підходи до доведення теореми, переконатися, що теорема Піфагора є дійсно Піфагоровою, побачити важливість теореми при використанні в інших галузях, для розв’язування задач прикладного характеру.

Завданнями є:

-дослідити, коли і ким було доведено теорему Піфагора;

-простежити різні підходи до доведення теореми;

-проаналізувати наслідки з теореми Піфагора;

-простежити використання теореми Пафагора для розв’язування задач практичного змісту.

РОЗДІЛ 1. БІОГРАФІЯ ПІФАГОРА.

Легендою і джерелом дискусій Піфагор (додаток А) став уже в стародавні часи. У 306 році до н.е. йому, як найрозумнішому з греків, поставили пам’ятник в римському форумі. З тих часів мало що прояснилося в біографії Піфагора.

Великий вчений Піфагор Самоський народився біля 580 р до н.е. на острові Самоса, біля узбережжя Малої Азії. Його батько Мнесарх із знатного, але збіднілого роду, був каменерізом. Ім’я матері Піфагора невідоме. За античними свідченнями хлопчик був казково красивим, а незабаром проявив і свої таланти. Серед учителів Піфагора часто звучить ім’я старця Гермодаманта і Ферекіда Сіроського (хоча достовірних фактів немає). Захопленням малого Піфагора були музика і поезія великого Гомера. Це захоплення збереглося на все життя.

Незабаром невгамовному уявленню юного Піфагора стало тісно на маленькому Самосі, він відправляється в Мілет, де зустрічається з іншим вченим – Фалесом. Саме Фалес радить йому відправитись за знаннями в Єгипет, що Піфагор і зробить.

За переказами, Піфагор років 20 перебував в Єгипті, а потім ще 10 років у Вавилоні, де ознайомлювався з математичними знаннями, які було нагромаджено в цих країнах протягом тисячоліть.

Піфагор повертається на Самос, де в цей час править тиран Полікрат. Звичайно ж, Піфагора не влаштовує  життя придворного раба, тому він перебирається в печери в окрузі Самоса. Після кількох місяців поневірянь Піфагор переселяється в Кротон, де засновує філософську школу – «Союз піфагорійців» (додаток Б). Це був одночасно і релігійний союз, і політичний клуб, і наукове товариство. Але потрібно відмітити, що деякі принципи, які проповідував Піфагор, можна наслідувати і сьогодні.

Пройшло 20 років. Слава про школу рознеслася по всьому світу. Одного разу до Піфагора прийшов Кілон, людина багата, але зла, і намагався сп’яну вступити до школи. Отримавши відмову, Кілон починає боротьбу з Піфагором і підпалює його дім. Піфагорійці спасли життя своєму вчителя ціною свого. Такого удару долі  Піфагор не витримав і незабаром покінчив життя самогубством.

Відкриття теореми Піфагором оточене ореолом красивих легенд.

Прокл, коментуючи останнє продовження першої книги “Начал” Евкліда, пише: “Якщо послухати тих, хто повторює давні легенди, то доводиться сказати, що ця теорема  походить від Піфагора; розповідають, що він у честь цього відкриття приніс у жертву бика”. Дехто розповідає, що він приніс у жертву не одного бика, а цілу сотню.

І хоча ще Цицерон помітив, що будь-яке кровопролиття було проти закону піфагорійського ордену, легенда ця зрослася з теоремою Піфагора і через більш, ніж 2000 років, продовжувала викликати гарячі відгуки.

Сьогодні теорема Піфагора виявлена у різних часткових задачах та кресленнях: і в єгипетському трикутнику, в папірусі часів фараона Аменемхета першого (біля 2000р. до н. е.), і у вавилонських клинописних табличках епохи царя Хаммурапі (XVIII ст. до н. е.), і в давньоіндійському трактаті VII-V ст. до н. е. “Сульва сутра”. У найдавнішому китайському трактаті “Чжоу-бі суань цзинь”, час створення  якого точно не відомо, стверджується, що в XII ст. до н. е. Китайці знали властивості єгипетського трикутника, а до VI ст. до н. е.- й загальний вигляд теореми. Не дивлячись на це, ім’я Піфагора щільно злилося з теоремою Піфагора. Сьогодні прийнято вважати, що Піфагор (додаток В) першим довів теорему, яка носить його ім’я. На жаль,  його доказ не дійшов до нашого часу. 

РОЗДІЛ 2. НЕАЛГЕБРАЇЧНІ ДОВЕДЕННЯ ТЕОРЕМИ

2.1. Найпростіше доведення

Розглянемо, які існують доведення теореми Піфагора, відомі із древніх трактатів. В шкільному підручнику ми знайомимось з алгебраїчним доведенням цієї теореми. При цьому безслідно зникає перше доведення теореми, яка вела древніх мудреців до істини.

«Квадрат, побудований на гіпотенузі прямокутного трикутника, рівновеликий сумі квадратів, побудованих на його катетах». Найпростіше доведення теореми отримаємо в спрощеному випадку, якщо прямокутний трикутник рівнобедрений. Напевне з нього і розпочалася теорема. Насправді, достатньо тільки подивитися на мозаїку рівнобедрених прямокутних трикутників (мал.1), щоб переконатися в справедливості теореми.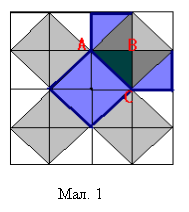

Наприклад, для △АВС: квадрат, побудований на гіпотенузі АС, містить чотири вихідних трикутники, а квадрати, побудовані на катетах, - по два. Теорема доведена.

2.2. Давнє китайське доведення

 Математичні трактати Древнього Китаю дійшли до нас з ІІ ст. до н.е. Справа в тому, що в 213 році до н.е. китайський імператор Ші Хуан-ді, намагаючись скасувати попередні традиції, наказав спалити всі древні книги. В ІІ ст. до н.е. в Китаї була винайдена бумага і почалось створення древніх книг. Так виникла тематика в дев’яти книгах – серед них математико – астрономічні твори. В книзі «Математика» розміщено креслення (мал. 2а), яке доводить теорему Піфагора. Ключ до доведення теореми за цим малюнком знайти не важко. На древнє китайському кресленні 4 рівних прямокутних трикутники з катетами a і b і гіпотенузою с складені так, що їх зовнішній контур утворює квадрат із стороною a+b, а внутрішній квадрат із стороною с, побудований на гіпотенузі (мал. 2б). Якщо квадрат із стороною с вирізати, чотири залишених зафарбованих трикутники скласти в два прямокутники (мал. 2в), то стане зрозуміло, що утворена порожнеча з однієї сторони рівна с², а з другої – a²+b², тобто c²=a²+b². Теорему доведено.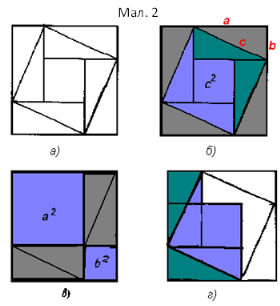

Таке доведення теореми досить незручне для застосування. Мабуть, давньокитайські математики мали інше доведення. А саме: якщо в квадраті із стороною с два зафарбованих трикутники (мал. 2б) відрізати і гіпотенузами прикласти до гіпотенуз двох інших трикутників (мал. 2г), то легко помітити, що отримана фігура, яку інколи називають «кріслом нареченої», складається з двох квадратів із сторонами a і b, тобто c²=a²+b².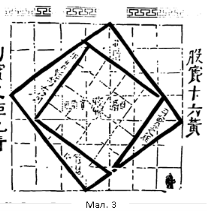

 На малюнку 3 зображено креслення із трактата «Чжоубі…» Теорема Піфагора розглянута для єгипетського трикутника з катетами 3 і 4 та гіпотенузою 5 одиниць виміру. Квадрат на гіпотенузі містить 25 клітинок, а вписаний в нього квадрат на більшому катеті – 16 клітинок, менший – 9 клітинок.

2.3. Древнє індійське доведення

 Математики Древньої Індії помітили, що для доведення теореми Піфагора досить використати внутрішню частину древньокитайського малюнка. В написаному на пальмових листах трактаті «Сіддханта Сіромані» («Вінець знань») знаменитого індійського математика ХІІ ст. Бхаскари  розміщене креслення (мал. 4а) з характерним для індійських доведень словом «Дивись!»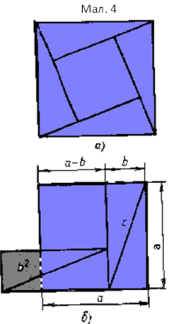

Як бачимо, прямокутні трикутники викладені гіпотенузою назовні і квадрат гіпотенузи с² перекладається і «крісло нареченої» a²+b² (мал. 4б). Часткові випадки теореми Піфагора ( наприклад, побудова квадрата, площа якого вдвічі більша площі даного квадрата), зустрічаються в древньоіндійському трактаті «Сульва Сутра» (VII —V ст. до н.е.)

2.4. Доведення Евкліда

Доведення Евкліда можна знайти в  47 припущенні  першої книги «Начал». На гіпотенузі і катетах прямокутнього трикутника АВС будуються відповідно квадрати (мал. 5) і доводиться, що прямокутник BJLD рівновеликий квадрату ABFH, а прямокутник JCEL – квадрату АСКG. Тоді сума квадратів на катетах буде рівна квадрату на гіпотенузі.

Насправді, зафарбовані на малюнку трикутники ABD і BFC рівні за двома стороними і кутом між ними: FB=AB BC=BD  <FBC=d+<ABC=<ABD. Але площа трикутника ABD рівна половині площі прямокутника BJLD, так як у трикутнику ABD і прямокутнику BJLD спільна основа BD і висота LD.

Аналогічно площа трикутника FBC рівна половині площі прямокутника ABFH (BF – спільна основа,  AB – спільна висота). Звідси, враховуючи, що площі трикутників рівні, маємо рівність площ і відповідних прямокутників.

Аналогічно, використовуючи рівність трикутників BCK і ACE, доводимо рівність площ прямокутників JCEL та ACKG.

 Отже, , що і потрібно було довести.

Доведення Евкліда, в порівнянні з древньокитайським або древньоіндійським виглядає доволі важким. По цій причині це доведення часто називають «ходульним» або «надуманим». Але така думка поверхнева. Малюнок, який використав Евклід для доведення теореми, жартома називають «піфагорові штани». На протязі довгого часу він вважався одним із символів математичної науки.

РОЗДІЛ 3. АЛГЕБРАЇЧНІ ДОВЕДЕННЯ ТЕОРЕМИ

3.1. Передумова

Дуже давно була придумана головоломка, яка сьогодні називається «Піфагор». Неважко переконатися в тому, що в основі семи частин головоломки лежать рівнобедренний прямокутний трикутник і квадрати, побудовані на його катетах, або, по-іншому, фігури, які складалися з 16 однакових рівнобедренних прямокутних трикутників і вкладалися в квадрат. Це лише невелика частинка багатства, яка захована в жемчужині античної математики – теоремі Піфагора.

3.2. Алгебраїчне доведення теореми.

Нехай ABC – прямокутний трикутник з катетами a і b та гіпотенузою c (мал. 6). Доведемо, що с²=a²+b² Побудуємо квадрат  зі стороною a+b. На сторонах квадрата візьмемо точки A, B, C, D так, щоб відрізки AB, BC, CD, DA відсікали від квадрата прямокутні трикутники. Позначимо їх Т₁, Т₂, Т₃, Т₄ з катетами a і b. Чотирикутник ABCD позначимо буквою Р. Покажемо, що Р – квадрат зі стороною с.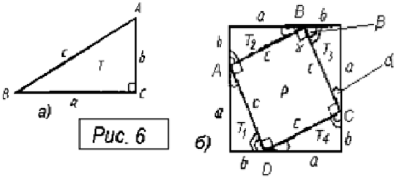

Всі трикутники Т₁, Т₂, Т₃, Т₄ рівні трикутнику Т (за двома катетами), тому їх гіпотенузи рівні гіпотенузі трикутника Т, тобто с. Доведемо, що всі кути цього чотирикутника прямі.

Нехай і - величини гострих кутів трикутника Т. Нам відомо, що . Кут при вершині А - чотирикутника Р разом з кутами  і утворює розгорнутий кут. Тому . Звідси . Аналогічно доводиться, що всі інші кути чотирикутника Р прямі. Отже, чотирикутник Р – квадрат зі стороною с.

Великий квадрат зі стороною a+b складається із квадрата Р зі стороною с і чотирьох трикутників, рівних трикутнику Т. Тому площа великого трикутника рівна сумі площ квадрата Р і чотирьох площ трикутника Т. Звідси _. З цієї рівності випливає, що

3.3. Доведення на основі подібності трикутників

У прямокутному трикутнику АВС проведемо висоту CD з вершини прямого кута С на гіпотенузу АВ, яка ділить його на два прямокутні трикутники ADC і DBC, подібні трикутнику АВС і подібні між собою (мал..7)  З того, що , маємо:, - катет АС прямокутного трикутника АВС є середнім пропорційним між гіпотенузою АВ і проекцією AD цього катета на гіпотенузу АВ.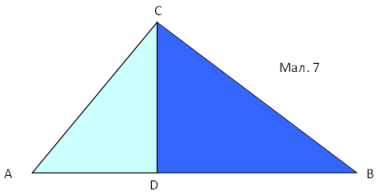

З того, що , маємо: , - катет ВС прямокутного трикутника АВС є середнім пропорційним між гіпотенузою АВ і проекцією BD катета ВС на гіпотенузу АВ. Якщо додати почленно ці рівності і врахувати, , дістанемо: .

Скориставшись тим, що , знаходимо .

У цьому випадку теорема Піфагора має формулювання: «Висота, проведена з вершини прямого кута на гіпотенузу, є середнім пропорційним між двома відрізками, на які вона поділяє гіпотенузу» або «Квадрат висоти, опущеної на гіпотенузу, дорівнює площі прямокутника, побудованого на відрізках гіпотенузи».

3.4. Доведення на основі поняття косинуса кута

У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів. Доведення.

 Нехай АВС – даний прямокутний трикутник з прямим кутом С. Проведемо висоту CD з вершини прямого кута С. (мал.8). За означенням косинуса кута . Звідси . Аналогічно , звідси . Додавши рівності почленно і врахувавши, , дістанемо . Теорему доведено.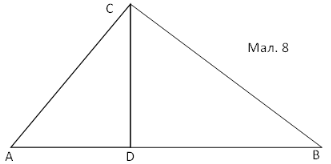

Теорему Піфагора для випадку рівнобедреного прямокутного трикутника іноді жартома називають «піфагоровими штанами» У Франції і Німеччині теорему Піфагора називали «ослячим мостом».

РОЗДІЛ 4. ЗАСТОСУВАННЯ ТЕОРЕМИ ПІФАГОРА

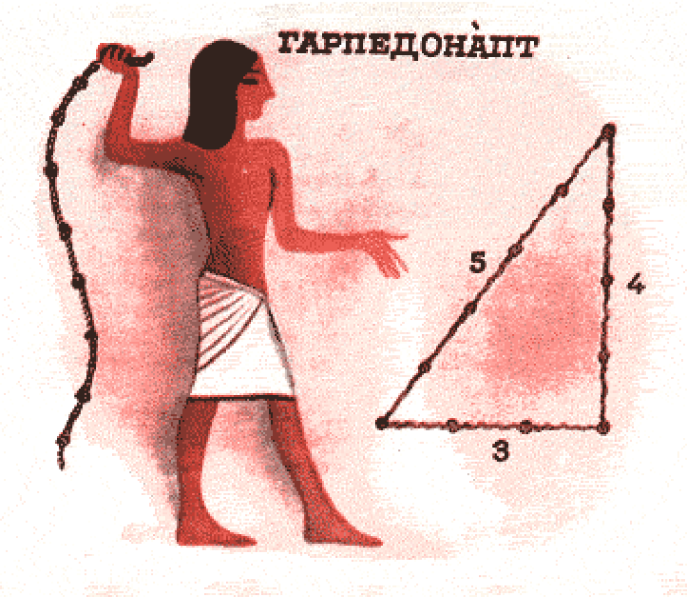
За два тисячоліття до нашої ери, ще до Піфагора, єгипетські землеміри будували прямий кут, встромивши кілки у землю і натягнувши у формі трикутника мотузку з вузлами на відстані 3, 4, 5 одиниць так, щоб вузли співпадали з кілками (додаток  Г). Такий трикутник називають «єгипетським», або «піфагоровим». У ньому , а кут, який лежить проти найбільшої сторони, прямий.

Цікаво, що саме такі пропорції археологи знаходять у розмірах тесаних плит піраміди Хефрена ( Греція).

Мабуть, роздумуючи над «єгипетським» трикутником, Піфагор почав шукати й інші прямокутні трикутники з цілочисловими сторонами. Прямокутні трикутники, у яких довжини всіх сторін виражаються цілими числами, називаються  піфагоровими трикутниками.

В давнину піфагоровим трикутникам надавали особливого значення, їм іноді приписували магічні властивості. Тепер відомо, що множина піфагорових трикутників нескінченна і є формули для визначення будь-якого з них.

Теорема Піфагора протягом багатьох століть була поштовхом до цікавих досліджень у геометрії. За теоремою Піфагора можна встановлювати метричні співвідношення між елементами не тільки прямокутного трикутника, а й інших фігур, які мають широке застосування.

Наприклад. Задача 1. Довести, що в довільному трикутнику квадрат сторони, яка лежить проти тупого кута, дорівнює сумі квадратів двох інших сторін, доданій до подвоєного добутку однієї з цих сторін на проекцію другої сторони на першу.

Доведення.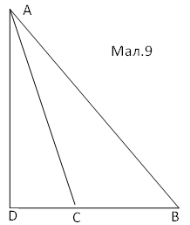

 Проведемо висоту AD з вершини А (мал.9). За теоремою Піфагора з трикутника ADB: , з трикутника ADC: .

Віднімаючи ці рівності почленно дістанемо:

. Врахувавши, що BD=BC+DC, матимемо

Задача 2. Довести, що в будь-якому трикутнику квадрат сторони, яка лежить проти гострого кута, дорівнює сумі квадратів двох інших сторін без подвоєного добутку однієї з цих сторін на проекцію другої сторони на першу.

Доведення аналогічне до першої задачі.

Задача 3. Довести, що в будь-якому паралелограмі сума квадратів діагоналей дорівнює сумі квадратів сторін. Доведення.

 Відомо, що в паралелограмі протилежні кути рівні, кожна діагональ розбиває його на два рівні трикутники, сума внутрішніх кутів, які прилягають до однієї сторони, дорівнює 180˚. Тому, якщо сторона АС трикутника АВС (мал. 10) лежить проти тупого кута, то сторона BD трикутника ADB лежить проти гострого кута. З даних трикутників маємо: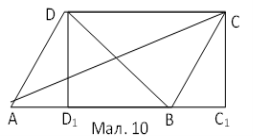

    

Додавши ці дві рівності почленно і врахувавши, що BC₁=AD₁ і AB=DC, дістанемо , що й потрібно було довести. Теорема Піфагора поширюється і на просторові фігури.

Важливість теореми Піфагора ілюструє такий цікавий факт. Наприкінці ХІХ ст. було відкрито на Марсі «канали», які тривалий час вважалися штучними. Для налагодження зв’язку з марсіянами запропонували на величезному просторі Західно – Сибірської низовини побудувати гігантську геометричну фігуру, яка б світилася, - малюнок теореми Піфагора, бо вважали, що ця теорема справедлива скрізь, і що жителі будь-якої планети повинні зрозуміти такий сигнал. Передбачали, що, побачивши це зображення, марсіяни  зроблять висновок, що на землі живуть розумні істоти і дадуть відповідь також мовою математики.

У 1955 році в Греції було випущено поштову марку, що ілюструє теорему Піфагора (додаток Д). Ілюстрації теореми Піфагора можна зустріти і на монетах (додаток Е), і на картинах сучасних художників (додаток Є). Теорема Піфагора широко використовується для розв’язування геометричних задач та задач прикладного характеру.

Задача 4. Драбину завдовжки 13 футів приставили до стіни так, щоб нижня її частина була віддалена від стіни на 5 футів. На скільки опуститься драбина по стіні, якщо її основу відсунути на 7 футів. (1 фут – 30,48см) (задача німецького рукописного трактату, який було складено не пізніше XVст).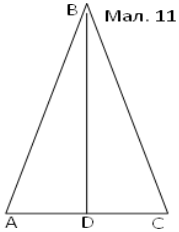

Задача 5. Ще в Древньому Вавилоні за допомогою теореми Піфагора обчислювали довжину висоти рівнобедреного трикутника за його основою і бічним ребром (мал. 11). AD=DC (BD- висота, медіана трикутника АВС.

Задача 6. У одного арабського математика ХІ ст.. знаходимо таку задачу:

На двох берегах річки росте по пальмі, одна навпроти другої. Висота однієї  30 ліктів, другої – 20 ліктів, відстань між їх основами – 50 ліктів. На верхівці кожної пальми сидить птах. Раптом обидва птаха побачили рибу, яка випливла на поверхню води між пальмами. Вони кинулись до неї разом і зловили її одночасно. На якій відстані від основ кожної пальми з’явилася риба. Розв’язування.

Нехай ВВ₁=30 ліктів, СС₁=20 ліктів, В₁С₁=50 ліктів. (мал. 12). Позначимо АВ₁=х ліктів, а АС₁=(50-х) ліктів. За теоремою Піфагора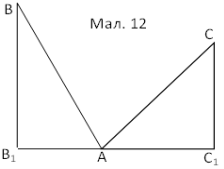

, Але АВ=АС, тому      

                    

Отже, риба з’явилась на відстані 20 ліктів від тієї пальми, висота якої 30 ліктів, а від пальми, висота якої 20 ліктів на відстані 30 ліктів.

Задача 7. При вимірювальних роботах в полі широко використовується сажень (польовий циркуль) – прилад у вигляді букви А. Висота його 1,37 м, ширина 2 м. Якої довжини необхідно взяти заготовки, щоб виготовити сажень.

(с²=1,37²+1²=1,8769+1=2,8769, с≈1,67. Отже, необхідно взяти дві заготовки по 1,67м).

ВИСНОВКИ

Теорема Піфагора дійсно «велика теорема». Вона перекладена на різні мови. На алегоричній мові езотерики  теорема Піфагора звучить «Як на небі, так і на Землі». Якщо на спеціальній програмі «відмотати» розміщення зірок в сузір’ї Оріона на 25000-30000 років назад, то отримаємо точну графічну конфігурацію теореми Піфагора. Повна картина комплексу пірамід в Гізі, Карнаці і Геліополісі точно повторює розміщення сузір’їв у Молочному шляху. Три Великих піраміди в Гізі – модель поясу сузір’я Оріону, що відповідає трикутнику теореми.

На англійській мові теорема звучить так: «The square on the hypotenuse is equal to the sum of the squares on the other two sides.»

Є також і такий варіант:

"I am, as you can see, a² + b² - ab

When two triangles on me stand,

Square of hypothenuse is plann'd

But if I stand on them instead

The squares of both sides are read.

Італійська мова: "Come potete vedere, sono a² + b² - ab

Quando ci sono due triangoli sopra di me

È rappresentato il quadrato dell'ipotenusa

Ma se invece sto io sopra di loro

Si leggono i quadrati dei due lati"

Французька мова:

Dans un triangle rectangle, le carré de l'hypoténuse (côté opposé
à l'angle droit) est égal à la somme des carrés des deux autres côtés.

Естонська мова: Valem sõnades:

täisnurkses kolmnurgas hüpotenuusi (c) ruut võrdub kaatetite (a ja b) ruutude summaga.

Дослівний переклад теореми в Евкліда: «В прямокутному трикутнику квадрат сторони, натягнутої над прямим кутом, рівний квадратам на сторонах, що стягують прямий кут».

Латинський переклад арабського тексту Аннаіріці (біля 900 р до н.е.), виконаний Герхардом Клемонським (початок 12 ст), в перекладі на російську мову звучить так : "Во всяком прямоугольном треугольнике квадрат, образованный на стороне, натянутой над прямым углом, равен сумме двух квадратов, образованных на двух сторонах, заключающих прямой угол".

В Geometria Culmonensis (біля 1400 р) в перекладі теорема читається так: "Итак, площадь квадрата, измеренного по длинной стороне, столь же велика, как у двух квадратов, которые измерены по двум сторонам его, примыкающим к прямому углу".

В першому російському перекладі евклідових «Начал», виконаним Ф. І. Петрушевским, теорема Піфагора викладена так: "В прямоугольных треугольниках квадрат из стороны, противолежащей прямому углу, равен сумме квадратов из сторон, содержащих прямой угол".

Від напівміфічного мудролюба нас відділяють тисячоліття. І одночасно нам зрозумілі і близькі загадки науки, людського буття, які хвилювали легендарного самосця. Йдучи шляхами пізнання, Піфагорові важко було не помилитися, все ж він та його учні допомогли людству зробити ще один крок до розкриття таємниць природи.

В результаті дослідження було виявлено, що теорема Піфагора була відома ще задовго до нього і існує близько 500 доведень цієї теореми. Одне з найдавніших походить з Індії, а відкриття та розуміння теореми проходило в декілька етапів. На думку Плутарха та Цицерона саме Піфагор зробив завершальний крок в її формулюванні та доведенні  За допомогою теореми Піфагора можна довести ряд геометричних тверджень, розв’язати прикладні задачі, задачі практичного характеру.

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ

 

1. Вейль Г. Теоретико – алгебраические исследования в математической физике - Київ, 1981.

2. Вивальнюк Л.М., Боровик В.Н. Математика. Посібник для факультативних занять у 9 класі: [навчальний посібник]  – Київ: Освіта. 1999.

3. Енциклопедичний словник юного математика – М.: Педагогіка, 1989

4. Зоря А.С., Кіро С.М. Про математику і математиків - К.: Радянська школа, 1981.

5. Кушнір І. А. Повернення втраченої геометрії [Текст] / І. А. Кушнір. – Київ: Факт, 2000. – 280с. – (Серія «Математичні обрії України»)

6. Кушнир И. А. Популярные доказательства теоремы Пифагора [Текст] / И.А.Кушнир. – Харьков: Вид.група «Основа», 2007. – 36 с. – ( Б-ка журн. «Математика в школах України»)

7. Матюшко І.С., Собко М.С. Завдання з геометрії для 8 класу – К.: Радянська школа, 1988.

8. Тадеєв В.О. Неформальна математика 6-9 класи – Тернопіль: Навчальна книга – БОГДАН, 2003.

Математичне моделювання: [Електронний ресурс]/режим доступу -

9. У світі математики: [збірник науково – популярних статей] / О. О. Колонькова. – Київ.: Радянська школа, 1974.

10. Елементи цікавої математики: [наук.- метод. посібник] / О.Г. Черватюк, Г.Д. Шиманська -  Київ: Радянська школа, 1968.-120 с.

11.  Білл Кассельман «Теорема Піфагора»: [Електронний ресурс] / режим доступу -https://uk.wikipedia.org/w/index.php?title=%D0%91%D1%96%D0%B B%D0%BB_%D0%9A%D0%B0%D1%81%D1%81%D0%B5%D0%BB%D1%8C%D0%BC%D0%B0%D0%BD&action=edit&redlink=1.

13. Богомільний О. Доведення теореми Піфагора (29 доведень); [Електронний ресурс] / режим доступу - https://peskiadmin.ru/uk/teorema-pifagora-pryamaya-razlichnye-sposoby-dokazatelstva.html.

Додаток А

 

Додаток Б

 

 

Додаток В

 

Додаток Г

 

 

 

Додаток Д

Додаток Е

 

Додаток Є