Теорема синусів і косинусів
Про матеріал
Презентація для ознайомлення з новим матеріалом.
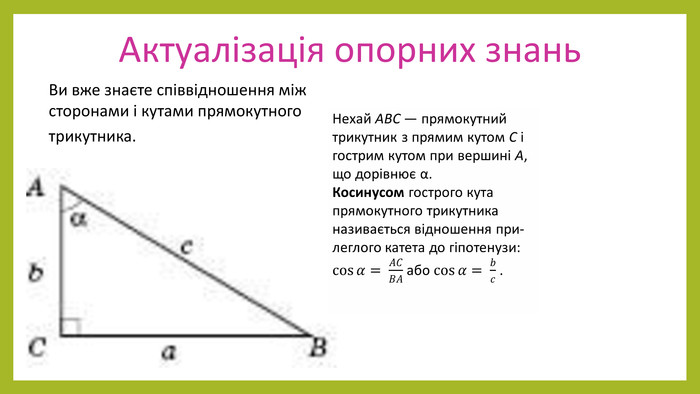
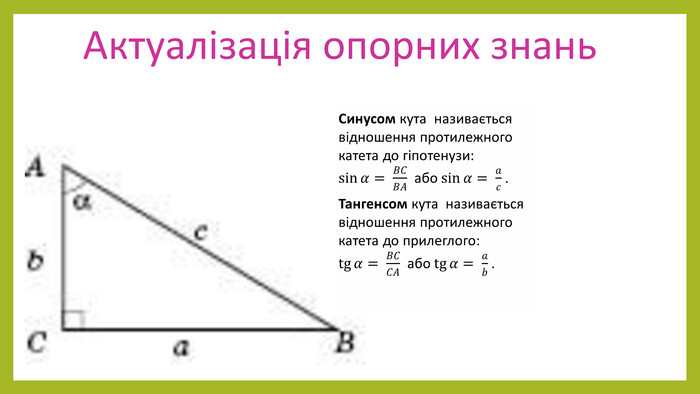
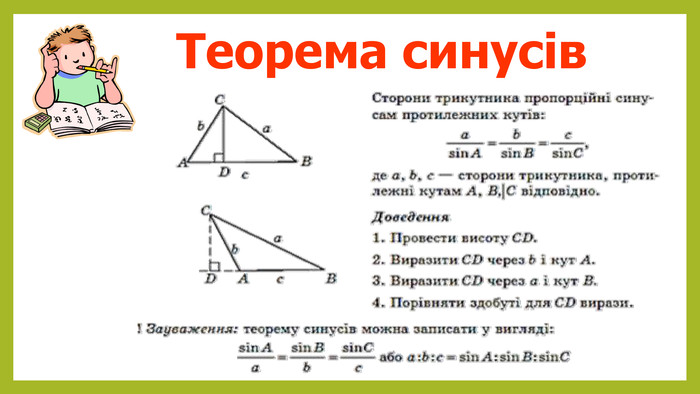
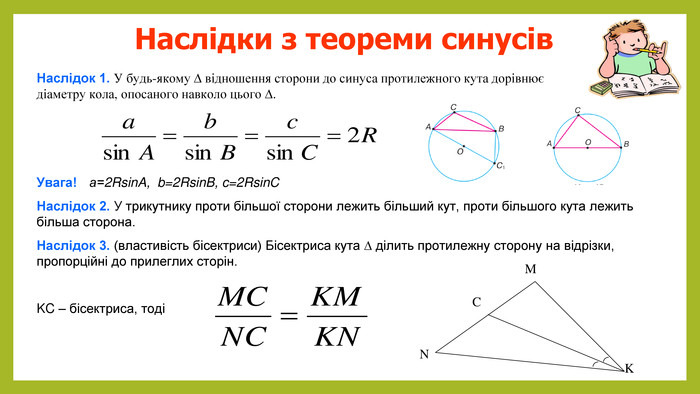
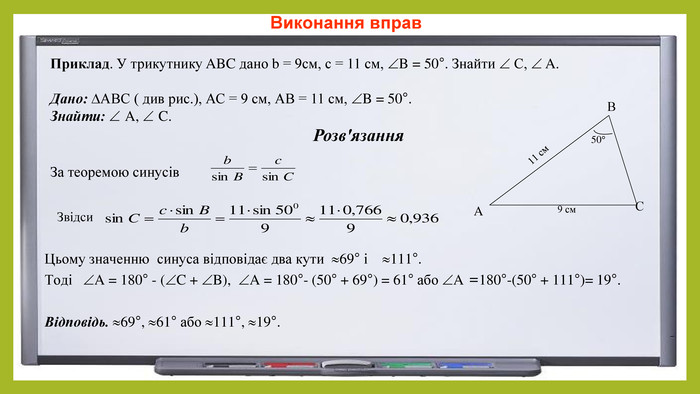
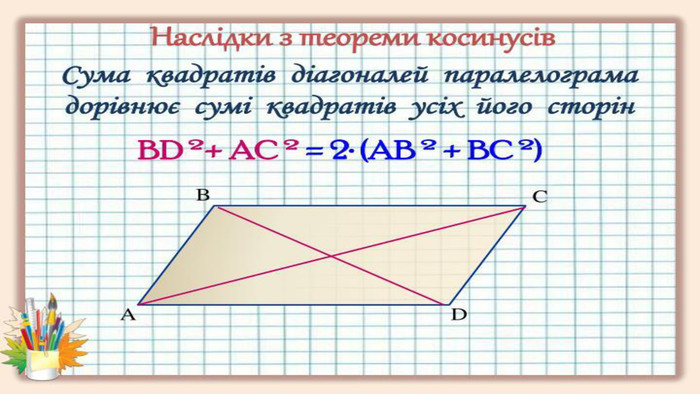
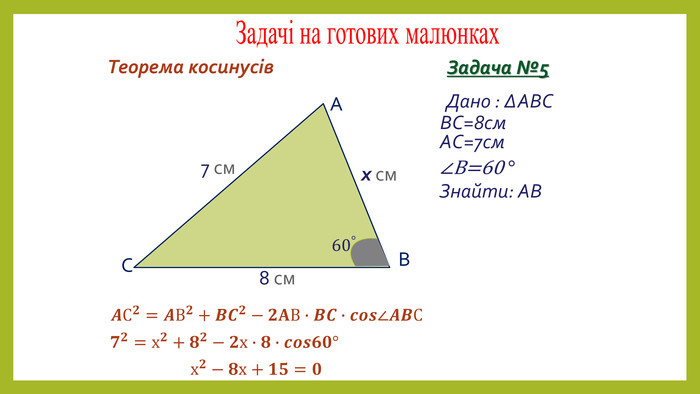
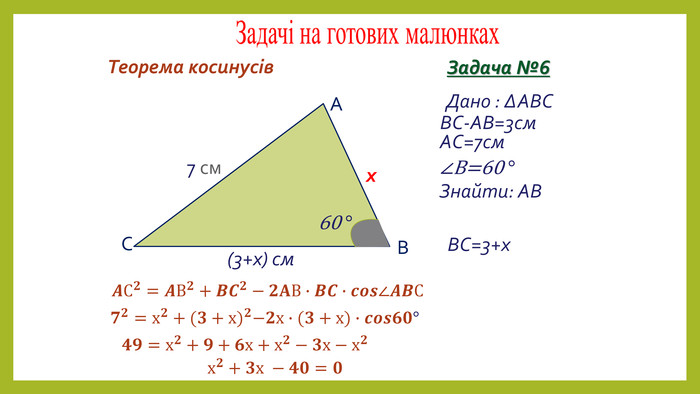
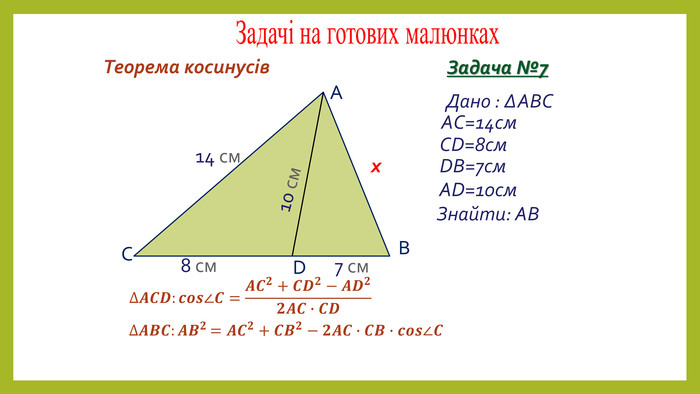
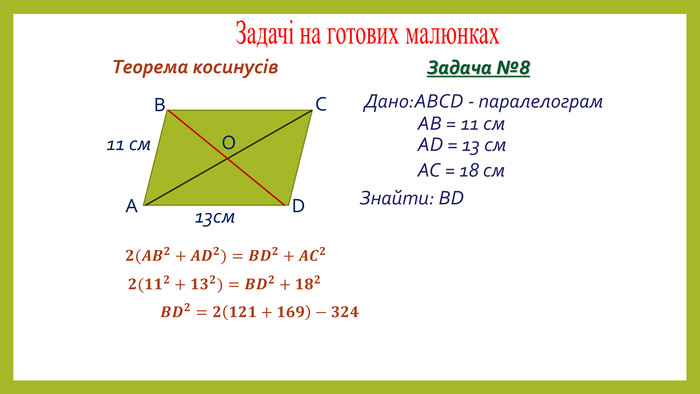
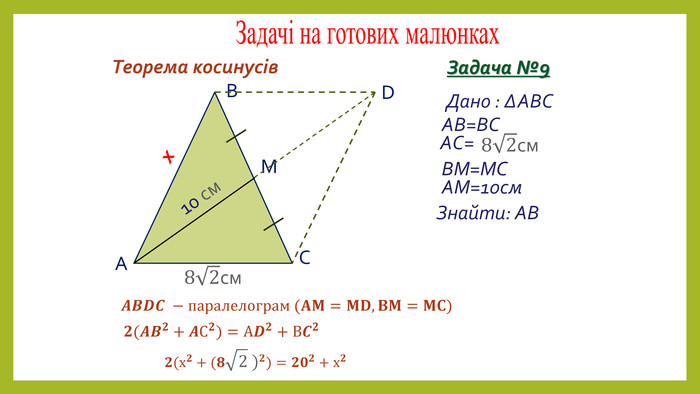
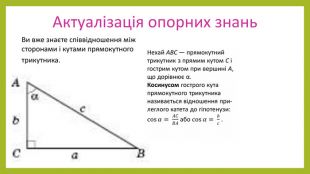
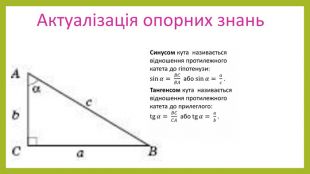
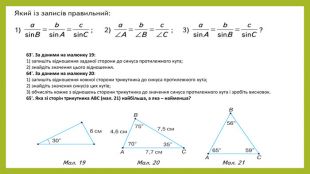
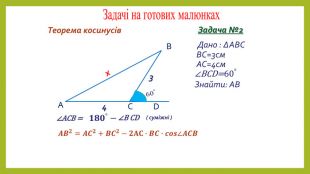
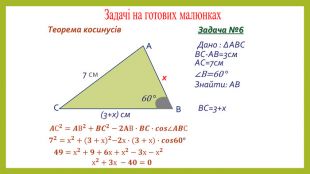
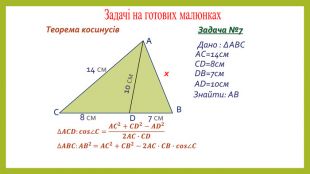
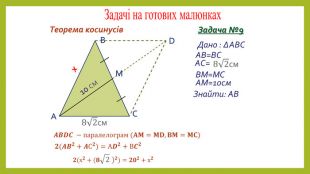
Презентація з геометрії для 9 класу на тему "Теорема синусів". Матеріали містять доведення теореми синусів,
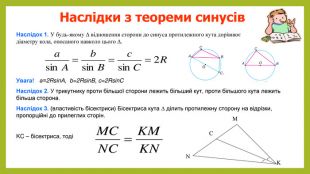
наслідки з теореми синусів, виконання усних вправ та розв'язування письмових задач. Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку