Урок "Вектори у просторі. Рівність векторів"

Тема уроку: Вектори у просторі. Рівність векторів

Мета уроку:

навчальна: формувати поняття вектора у просторі, рівних векторів, координат вектора; сформувати вміння розв'язувати задачі, що передбачають використання цих понять;

розвиваюча: розвивати логічне мислення; навички контролю, самоконтролю та   взаємоконтролю; спонукати до творчої діяльності.

виховна: виховувати любов до рідної мови та предмету; працьовитість, відчуття колективізму та відповідальності; вміння самостійно приймати рішення.

Тип уроку : засвоєння нових знань і вмінь

Обладнання: підручник, конспект по темі уроку.

План уроку

І. Організаційний момент

II. Перевірка домашнього завдання

III. Повідомлення теми уроку

IV. Сприймання і усвідомлення нового матеріалу

V. Розв’язування вправ

VI. Підсумок уроку

VІ. Повідомлення домашнього завдання

Хід уроку

  І. Організаційний момент

Вітаюсь з учнями. Перевіряю готовність класу до уроку (чистоту дошки, наявність крейди, ганчірки), з’ясовую хто черговий, відмічаю відсутніх.

  ІІ. Перевірка домашнього завдання

Домашнє завдання на 12.03.2020 р. за підручником Математика: алгебра і початки аналізу та геометрія, рівень стандарту: підруч. для 10 кл. закладів загальної середньої освіти / А. Г. Мерзляк, Д. А. Номіровський, В. Б. По-лонський, М. С. Якір. – Х. : Гімназія, 2018. – 256с. : іл.

Опрацювати §6 п.38, №38.10, №38.14.

  Вибірково перевіряємо виконання домашнього завдання  в учнів які потребують додаткової педагогічної уваги за матеріалом вивчених тем проводимо тестування

№38.10

Які з точок М (5; 10; -3), N (5; 9; 3), K (4; -9; 3), P (4; -9; 2) лежать в одній площині, паралельні площині xy?

 Точки  N (5; 9; 3) і K (4; -9; 3) лежать в одній площині, паралельні площині xy.

№38.14

Які з точок D (2; 3; 4), E (-2; 3; 4), K (2; 3; -4), M (-2; -3; 4) лежать на одній прямій, паралельній осі аплікат?

 Точки D (2; 3; 4) і K (2; 3; -4) лежать на одній прямій  паралельній осі аплікат.

ІII. Повідомлення теми уроку

ІV. Сприйняття й усвідомлення нового матеріалу

У  курсі  планіметрії  ви  вивчали  вектори  на  площині.  Тепер  ви починаєте  вивчати  вектори  в  просторі.  Багато  понять  і  властивостей,  пов’язаних  з  векторами  на  площині,  можна  майже  дослівно віднести  до  векторів  у  просторі.  Доведення  такого  роду  тверджень про  вектори  в  просторі  цілком  аналогічні  доведенням  відповідних тверджень про вектори на площині.

  Розглянемо  відрізок  AB.  Якщо  ми  домовимося  точку  A  вважати початком  відрізка,  а  точку  B  —  його  кінцем,  то  такий  відрізок  буде характеризуватися  не  тільки  довжиною,  але  й  напрямом  від  точки  A до  точки  B.  Якщо  вказано,  яка  точка  є  початком  відрізка,  а  яка точка  —  його  кінцем,  то  такий  відрізок  називають  напрямленим відрізком  або  вектором.

  Вектор  з  початком  у  точці  A  й  кінцем  у  точці  B  позначають  так: (читають:  «вектор  AB»).  Для  позначення  векторів  також  використовують малі букви латинського алфавіту зі стрілкою зверху.

  Вектори і називають однаково напрямленими, якщо однаково напрямлені півпрямі АВ і CD.

  Вектори і називають протилежно напрямленими, якщо протилежно напрямлені півпрямі АВ і CD.

  На  відміну  від  відрізка,  у  якого  кінці  —  різні  точки,  у  вектора початок і кінець можуть збігатися.

  Домовились  називати  вектор,  у  якого  початок  і  кінець  —  одна й  та  сама  точка,  нульовим  вектором  або  нуль-вектором  і  позначати   .

  Модулем ( або довжиною)  вектора  називають  довжину  відрізка  AB. 

  Позначають: Вважають, що  модуль  нульового  вектора  дорівнює  нулю.  Записують: .

 Два вектори називаються рівними, якщо вони мають однакові довжину і напрям.

 Координатами вектора з початком у точці А (x₁; y₁; z₁) і кінцем у точці В (x₂; y₂; z₂) називають упорядкований набір чисел: x₂-x₁; y₂-y₁; z₂-z₁.

  Так само як і на площині, обґрунтовують, що рівні вектори мають рівні відповідні координати і, навпаки, вектори, які мають рівні відповідні координати, є рівними. Це дає підставу для позначення вектора його координатами: (а₁; а₂; а₃) або просто .

  V. Розв’язування вправ

№ 39.1

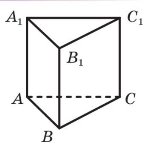На рисунку 39.5 зображено призму ABCA₁B₁C₁, основою якої є правильний трикутник. Чи є рівними вектори:

1) і   (так)

2)  і (ні)

3) і (ні)

4) і (так)

№2

Дано чотири точки А ( 1; 5; -4), В ( 2; -1; 3), С (-3; 1; 2), D (-4; 7; -5).

1) Укаєіть серед векторів , , і рівні вектори.

2) Знайдіть довжини векторів і .

Розв’язання

1) Рівні вектори мають рівні відповідні координати. Тому для розв’язання задачі знайдемо координати вказаних векторів і виберемо з них пари рівних векторів (для знаходження координат вектора треба від координат кінця вектора відняти відповідні координати початку).

Знайдемо координати заданих векторів:

(1; -6; 7), ( -5; 2; -1), (1; -6; 7), (-5; 2; -1). Тоді:

1) = і = ;

2) ,

    .

№ 39.15 (додатково)

Модуль вектора (-4; у; 12) дорівнює 13. Знайдіть значення у.

Розв’язання

Маємо: (-4; у; 12)

,

,

,

.

Отже, (-4; -3; 12) або (-4; 3; 12).

№4 (додатково)

Знайдіть координати вершини D паралелограма ABCD, якщо А (3; 2; -1), В (5; -4; 7), С (-1; 2; 6).

Розв’язання

 Якщо ABCD – паралелограм, то в нього протилежні сторони (наприклад, ВС і АD) паралельні і рівні, але тоді й вектори і є рівними, а отже, є рівними й відповідні координати цих векторів.

  Нехай точка D має координати D (x; y; z). Тоді вектори і мають координати: (x-3; y-2; z+1), (-6; 6; -1).

  Оскільки ABCD – паралелограм, то =. Рівні вектори мають рівні відповідні координати, тому х-3 = -6, у-2=6, z+1= -1. Звідси х = -3, у = 8, z = -2. Тоді точка D має координати D (-3; 8; -2).

VI. Підсумок уроку

Фронтальне опитування:

1. Дайте означення вектора;

2. Дайте означення довжини вектора;

3. Дайте означення рівних векторів;

4. Дайте означення координат вектора;

5. Запишіть формулу для знаходження довжини вектора (а₁; а₂; а₃).

VІ. Повідомлення домашнього завдання

Опрацювати §6 п.39, №39.8, №39.10, №39.16.