"Звичайний дріб". Теоретичний матеріал до уроку в 5 класі.

Урок №1

Любий друже, на сьогоднішньому уроці, ти знайдеш відповіді на такі запитання:

• Що таке звичайний дріб?
• Як записується звичайний дріб?
• Що таке «чисельник» та «знаменник»?
• Як записувати дробове число?

Буває так, що нам потрібно для розрахунку не ціле число, а тільки якась його частина. Саме коли ми, ділимо щось ціле на декілька рівних частин, ці частини можна назвати дробовим числом. Наприклад: Аркуш паперу розрізали на 4 рівні частини. Кожна з цих частин буде 1 часткою з чотирьох від цілого аркуша. А, якщо, ми знову складемо всі частинки, на які розділили аркуш, то отримаємо один цілий аркуш паперу. Такі частини від одного цілого ми записуємо за допомоги дробового числа. Дробове число складається із чисельника, знаменника та дробової риски. Чисельник та знаменник записують за допомоги натуральних чисел. Знаменник знаходиться під дробовою рискою та вказує на скільки рівних частин було розділено одне ціле.

-  одне ціле розділили на 4 рівні частини;

Чисельник вказує, скільки рівних частин, від одного цілого, взяли

– 1 частину з 4 було взято;

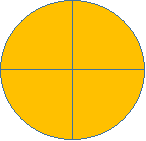
 Фігуру було розділено на 4 рівних частини;

 Взяли 3 частини з чотирьох.

Таке число можна записати у вигляді звичайного дроба , де 3-чисельник, що вказує на те, що було взято 3 частини, а 4 – знаменник, який показує на скільки частин було розділено фігуру.

Запис виду називається звичайний дріб. 

Розглянемо приклади звичайного дробу:

1. Пиріг розділили на 10 шматків та кожному гостю дали по одному, таке число буде записано у вигляді звичайного дробу таким чином: ;
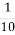2. Город розділили на 6 різних ділянок  під посадку овочів. Для картоплі виділили дві ділянки з 6. Такий звичайний дріб записується як ;
3. Апельсин має 8 часточок, брат взяв собі три часточки, що можна представити у вигляді , а сестрі віддав інші 5 часточок, що має вигляд .

Подивіться на малюнок, перед нами фігури, які розділені на однакові частини. Що б встановити, який саме звичайний дріб перед нами, треба підрахувати, на скільки частин розділено фігуру, це буде наш знаменник. Кількість взятих нами рівних частин від всієї фігури зафарбуємо в сірий колір. Скільки частин зафарбовано, стільки складатиме наш чисельник.

Отже, якщо записати це у вигляді дробу, то отримаємо:

1) ;      2) ;     3);    4) ;  5)   6) ;   7) ; 8); 9) ; 10); 11) ; 12) ;

Якщо чисельник та знаменник однакові, то такий звичайний дріб дорівнює одному. Тому що, якщо одне ціле поділити на декілька однакових частин, і всі ці частини взяти, то можна сказати, що ми взяли одне ціле.

  = 1;

Дріб, у якого чисельник менший від знаменника, називається правильним.

Дріб, у якого чисельник більший за знаменник або дорівнює йому, називається неправильним.

Приклади правильного дробу: ; ;;;

Приклади неправильного дробу: ; ;;

Якщо, чисельник і знаменник дробу замінити буквами, то,  дріб  є правильним, якщо a < b, і неправильним, якщо a ≥ b.

Вправа 1

Встановіть, яку частину тижня становить один день.

Розв’язання:

У тижні 7 днів, значить, можна уявити, що тиждень розділено на 7 рівних частин. Один день становить одну частину із 7. Значіть можна записати це як .

Вправа 2.

Запишіть всі правильні дроби зі знаменником 5.

Розв’язання:

Правильними дробами називають такі дроби, в яких чисельник менше знаменника. Тому, якщо знаменник 5, чисельник має бути натуральним число менше за 5. Такими дробами будуть:; ; ; ;

Можна зробити висновок, що звичайні дроби потрібні нам для розрахунків не цілого, а його окремих однакових частин. Дріб складається з чисельника, знаменника та дробової риски. Знаменник вказує на скільки частин розділили ціле, а чисельник-скільки таких частин взяли.

Ключові терміни і поняття:

 Звичайний дріб; чисельник; знаменник;