Теоретичний матеріал на тему "Геометричні тіла"
МНОГОГРАННИКИ
Многогранник − це геометричне тіло, поверхня якого складається із скінченого числа плоских многокутників.
Гранями многогранника називаються частини площин (многокутники), які обмежують многогранник.
Ребрами многогранника називаються спільні сторони суміжних граней (многокутників).
Вершинами многогранника називаються вершини многогранних кутів, утворених його гранями, що сходяться в одній точці.
Діагоналлю многогранника називається відрізок прямої, яка сполучає дві вершини многогранника, що не лежать в одній грані.
Діагональною площиною многогранника називається площина, що проходить через три вершини многогранника, які не лежать в одній грані.
Перерізом многогранника площиною називається частина цієї площини, яка обмежена лінією перетину поверхні многогранника з цією площиною.
Усі многогранники − це тіла, обмежені площинами. Введені позначення: Vоб’єм тіла, Sплоща повної поверхні, S0 площа основи,Sб – площа бічної поверхні, h – висота.
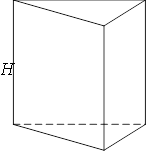 1. Призма − це тіло, основи якого − рівні многокутники, а бічні грані − паралелограми. Якщо ребра перпендикулярні до площини основи, то призма називається прямою. Якщо пряма призма в основі має правильні многокутники, то вона називається правильною.
1. Призма − це тіло, основи якого − рівні многокутники, а бічні грані − паралелограми. Якщо ребра перпендикулярні до площини основи, то призма називається прямою. Якщо пряма призма в основі має правильні многокутники, то вона називається правильною.
V S0Н − об’єм призми;
S Sб 2S0 − площа повної поверхні;
Sб Росн Н − площа бічної поверхні.
|
V abc − об’єм паралелепіпеда; S2(abbcac) − площа повної поверхні.
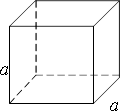
3. Куб − це прямокутний паралелепіпед, у |
а
|
|
S 6a2 − площа повної поверхні куба. |
а
|
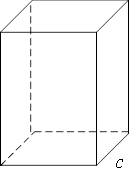
 2. Паралелепіпед − це призма, основами якої є паралелограми. Прямий паралелепіпед, основи якого утворені прямокутниками, нази-
2. Паралелепіпед − це призма, основами якої є паралелограми. Прямий паралелепіпед, основи якого утворені прямокутниками, нази-
вається прямокутним з ребрами a, b, c.
b В паралелепіпеді всі діагоналі d рівні між собою і задовольняють умову: d2 a2 b2 c2.
якого a b c.
![]() da 3 − діагональ куба;
da 3 − діагональ куба;
V a3 − об’єм куба;
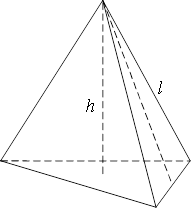 4. Піраміда − це тіло, основа якого − многокутник, а бічні грані − трикутники, що збігаються в одній вершині.
4. Піраміда − це тіло, основа якого − многокутник, а бічні грані − трикутники, що збігаються в одній вершині.
Висота будь-якої бічної грані називається апофемою. Якщо основа піраміди − правильний многокутник, а висота проходить через центр основи, то піраміда називається правильною, а її бічні грані − рівнобедрені трикутники.
V 1S0h – об’єм піраміди;
3
Sпов Sосн Sб – площа повної поверхні.
Sб ![]() Рl – площа бічної поверхні; Р – периметр основи, l – апофема.
Рl – площа бічної поверхні; Р – периметр основи, l – апофема.
Якщо всі грані і основа рівносторонні трикутники, то піраміда називається тетраедром.
2


про публікацію авторської розробки
Додати розробку
