Теоретичний матеріал "Нерівності зі змінними. Розв'язування лінійних нерівностей та їх систем"

1. Нерівності зі змінними. Розв’язок нерівності. Числові проміжки

1.1

Нерівність, яка містить невідоме, називають нерівністю зі змінною.

1.2

Розв'язком нерівності з однією змінною називають значення змінної, яке перетворює її у правильну числову нерівність.

1.3

Розв'язати нерівність означає знайти всі її розв'язки, або довести, що їх немає

1.4

Усі розв'язки нерівності утворюють множину розв'язків нерівності.

1.5

Якщо нерівність розв'язків немає, то кажуть, що множиною її розв'язків є порожня множина – 

1.6

Дві нерівності називаються рівносильними, якщо вони мають одну й ту саму множину розв’язків.

               і

1.7

Множину розв'язків нерівності називають числовим проміжком.

1.8

Якщо точки – кінці проміжку включені в проміжок, їх позначають зафарбованими кружечками, якщо не включені – порожніми кружечками (їх ще називають «виколотими» точками).

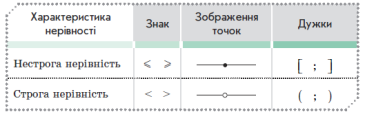
Якщо точки – кінці проміжку включені в проміжок, то для запису використовують квадратні дужки, якщо не включені – круглі дужки.

2. Розв’язування лінійних нерівностей

2.9

Нерівності виду називаються лінійними нерівностями з однією змінною.

2.10

Властивості, які використовуються під час розв’язування нерівностей:

1. Якщо з однієї частини нерівності перенести в іншу доданок з протилежним знаком, то утвориться нерівність, рівносильна даній.
2. Якщо обидві частини нерівності помножити або поділити на одне й те саме додатне число, то утвориться нерівність рівносильна даній.
3. Якщо обидві частини нерівності помножити або поділити на одне й те саме від’ємне число, змінивши при цьому знак нерівності на протилежний,  то утвориться нерівність рівносильна даній.

3. Розв’язування систем лінійних нерівностей

3.11

Якщо необхідно знайти спільні розв’язки двох чи більше нерівностей, то говорять, що треба розв’язати систему нерівностей.

3.12

Розв’язком системи нерівностей з однією змінною називають значення змінної, при якому правильною є кожна з нерівностей системи.

3.13

Розв’язати систему нерівностей з однією змінною означає знайти всі її розв’язки або довести їх немає.

3.14

Схема розв’язування систем нерівностей

1. Розв’язати кожну нерівність системи.
2. Зобразити множину розв’язків кожної з нерівностей на координатній прямій.
3. Знайти переріз цих множин, який і буде множиною розв’язків системи.
4. Записати відповідь.

4. Розв’язування подвійних нерівностей

4.15

Щоб розв’язати подвійну нерівність потрібно записати її у вигляді системи двох нерівностей і розв’язати цю систему.