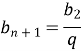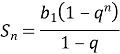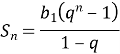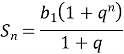Тест «Числові послідовності. Арифметична та геометрична прогресія.» 11 клас
Однією з умов засвоєння програмового матеріалу є міцне засвоєння теоретичного матеріалу. Важливо привчати учнів систематично працювати з підручником, не тільки виконуючи практичні вправи, а й засвоюючи теоретичний матеріал. Пропоную даний тест для перевірки засвоєння теоретичних знань для учнів 11класу на повторення по темі "Числові послідовності. Арифметична та геометрична прогресія". Тест має чотири варіанти відповіді, із яких лише одна правильна . Учню пропонується із вказаних варіантів відповідей вибрати тільки одну правильну і занести букву, під якою вона стоїть у бланку відповідей .
Тест для повторення при підготовці до ЗНО по темі «Числові послідовності. Арифметична та геометрична прогресія.»
- Що називають послідовністю?
|
А |
Б |
В |
Г |
|
функцію, яка за-дана на множині всіх цілих чисел |
функцію, яка за-дана на множині всіх дійсних чисел |
функцію, яка задана на множині всіх, або пер-ших n натуральних чисел |
множина натураль-них чисел |
- Числа, які утворюють послідовність називають
|
А |
Б |
В |
Г |
|
вільними членами |
коефіцієнтами послідовності |
коефіцієнтами |
членами послідовності |
- Який спосіб задання послідовності називається рекурентним?
|
А |
Б |
В |
Г |
|
за допомогою переліку чле-нів послідов-ності |
за допомогою задання опису знаходження її членів |
вказавши пер-ший та остан-ній члени послідовності |
вказавши перший, або кілька перших членів по-слідовності, та умову, за якою можна визначити будь-який її член |
- Що називається арифметичною прогресією?
|
А |
Б |
В |
Г |
|
послідовність |
послідовність,кожний член якої, починаючи з другого, дорівнює попередньому члену, до якого додається одне й те ж число |
послідов-ність, кож-ний член якої дорів-нює попе-редньому |
послідовність,кожний член якої, починаючи з другого, дорівнює попередньому члену, помноженому на одне й те ж число |
- Яка з формул є рекурентною формулою арифметичної прогресії?
|
А |
Б |
В |
Г |
|
|
|
|
|
- Будь-який член арифметичної прогресії, починаючи з другого
|
А |
Б |
В |
Г |
|
дорівнює попердньому |
є середнім геометричним двох попередніх |
є середнім геомет-ричним поперед-нього і наступного |
є середнім арифмет-ичним поперед-нього і наступного |
- Сума двох членів скінченної арифметичної прогресії , які рівновіддалені від її крайніх членів дорівнює
|
А |
Б |
В |
Г |
|
сумі крайніх членів прогресії |
сумі крайніх членів прогресії, поділеній на два |
добутку крайніх членів прогресії |
квадратному кореню з добутку крайніх членів прогресії |
- Яка з формул є формулою n-го члена арифметичної прогресії?
|
А |
Б |
В |
Г |
|
|
|
|
|
- Суму n перших членів арифметичної прогресії можна знайти за формулою
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Послідовність із загальним членом
|
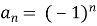
А |
Б |
В |
Г |
|
є зростаючою |
є спадною |
є необмеженою |
є ні зростаючою, ні спадною |
- Арифметична прогресія є зростаючою послідовністю. Яку умову задовольняє її різниця d ?
|
А |
Б |
В |
Г |
|
0<d<1 |
d>1 |
d=1 |
d>0 |
- Послідовність, яка має нескінченне число членів називається
|
А |
Б |
В |
Г |
|
обмеженою |
нескінченною |
скінченною |
зростаючою |
- Послідовність, елементами якої є числа називається
|
А |
Б |
В |
Г |
|
зростаючою |
телевізійною |
спортивною |
числовою |
- Арифметичною прогресією є послідовність, що задана формулою
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Послідовність задана формулою n-го члена
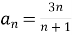. Її перший член дорівнює
|
А |
Б |
В |
Г |
|
3 |
1,5 |
2 |
|
-
Послідовність задана рекурентно
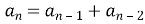,то
|
А |
Б |
В |
Г |
|
|
|
|
|
- Частка від ділення будь-якого члена геометричної прогресії, починаючи з другого, на попередній член дорівнює
|
А |
Б |
В |
Г |
|
першому члену |
знаменнику q |
різниці d |
другому члену |
-
Яка формула є рекурентною формулою геометричної прогресії, за умови, що відомо
?
|
А |
Б |
В |
Г |
|
|
|
|
|
- Квадрат будь-якого члена геометричної прогресії, починаючи із другого, дорівнює
|
А |
Б |
В |
Г |
|
|
добутку двох су-сідніх з ним членів |
сумі двох сусідніх з ним членів |
добутку двох попередніх членів |
сумі двох попе-редніх членів |
|
- Добуток двох членів геометричної прогресії, рівновіддалених від її крайніх членів, дорівнює
|
А |
Б |
В |
Г |
|
сумі крайніх членів прогресії |
сумі крайніх членів прогресії, поділеній на два |
добутку крайніх членів прогресії |
квадратному кореню з добутку крайніх членів прогресії |
- Яка з формул є формулою n-го члена геометричної прогресії?
|
А |
Б |
В |
Г |
|
|
|
|
|
- Суму n перших геометричної прогресії можна знайти за формулою
|
А |
Б |
В |
Г |
|
|
|
|
|
- Яка геометрична прогресія називається нескінченною?
|
А |
Б |
В |
Г |
|
|
|
|
|
- За якою формулою обчислюють суму нескінченної геометричної прогресії?
|
А |
Б |
В |
Г |
|
|
|
|
всі відповіді правильні |
- Геометричною прогресією називається
|
А |
Б |
В |
Г |
|
послідов-ність |
послідовність, кожний член якої, починаючи з другого, дорівнює по-передньому члену, до якого додається одне й те ж число |
послідовність кожний член якої дорівнює попередньому |
послідовність, кожний член якої, починаючи з другого, дорівнює по-передньому члену, по-множеному на одне й те ж число |
-
Геометричну прогресію задано формулою n-го члена
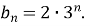Її другий член дорівнює
|
А |
Б |
В |
Г |
|
6 |
2 |
18 |
54 |
- n-ий член геометричної прогресії 2,-6,… дорівнює
|
А |
Б |
В |
Г |
|
2∙ |
2∙ |
2∙ |
2∙ |
-
Сума n-перших член геометричної прогресії дорівнює
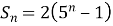, то третій член дорівнює
|
А |
Б |
В |
Г |
|
0 |
48 |
200 |
248 |
-
Сума прогресії
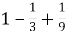- …дорівнює…
|
А |
Б |
В |
Г |
|
|
|
|
|
- Чому дорівнює сума n- перших членів геометричної прогресії, якщо знаменник прогресіїї дорівнює 1, а перший член дорівнює b
|
А |
Б |
В |
Г |
|
|
|
|
b-n |
- Яким способом не можна задати послідовність?
|
А |
Б |
В |
Г |
|
описом |
переліком її членів |
таблицею |
пейзажем |
про публікацію авторської розробки
Додати розробку