Довідничок-помічничок "Готуємось до ЗНО. Звичайні дроби"

Готуємось до ЗНО. Звичайні дроби

 

 1.1. Звичайні дроби;

    - долі одиниці;

    - дробові числа;

    - зображення дробу.

1.2. Арифметичні дії над звичайними дробами;

    - додавання;

    - віднімання;

    - множення;

    - множення мішаних чисел;

    - ділення дробів;

    - ділення змішаних чисел.

1.3. Основні типи задач на дроби.

    - знаходження дробу від числа.

       1.4. Завдання для практичних навичок

 

1.1. Звичайні дроби

Дробові числа. Число, складене з однієї або декількох рівних частин одиниці, називається дробом (звичайним дробом). Наприклад, (одна десята), (три п’ятих), (дванадцять сьомих)– дроби.

Числа, до складу яких входять цілі числа і дріб, називають мішаними.

Приклад. Якщо 5 яблук розділити між двома хлопцями, то число яблук у кожного хлопця виразиться цілим числом і деяким дробом (половиною), тобто мішаним числом.

Дроби і мішані числа разом називають дробовими числами.

Отримують дробові числа в результаті виміру і ділення.

Зображення дробу. Дріб зображають за допомогою двох натуральних чисел і риски дробу. Під рискою пишуть число, що показує, на скільки частин розділена одиниця. Воно називається знаменником дробу. Над рискою пишуть число, що показує скільки таких частинок міститься в дробі. Воно називається чисельником дробу.

Чисельник і знаменник називаються - членами дробу.

Приклад. У дробі чисельник рівний 7, а знаменник 5. Читають дроби так: спочатку називають чисельник, потім - знаменник. — ”дві сьомих”.             

Мішані числа зображають так: спочатку пишуть ціле число, а потім поряд із

ним справа приписують дріб.

Приклад. Мішане число ”дві цілих і чотири п’ятих“ записують так: .

Правильні і неправильні дроби. Розрізняють дроби правильні і неправильні. Дріб називають правильним , якщо його чисельник менший знаменника. Якщо ж чисельник більший знаменника або рівний йому, такий дріб називається неправильним.

Приклад. Дроби - правильні; - неправильні.

Правильний дріб менший за одиницю, а не правильний - більший або рівний одиниці.

Щоб перетворити неправильний дріб в мішане число, потрібно чисельник дробу розділити на знаменник і знайти остачу, частка покаже число цілих одиниць, а остача - число долей одиниці.

Приклад. , так як 20 : 3 = 6(остача 2).

Щоб перетворити мішане число в неправильний дріб, потрібно знаменник помножити на ціле число,а до отриманого добутку додати чисельник. Зробити цю суму чисельником шуканого дробу, при цьому знаменник залишити той же.

Приклад. .

 

Порівняння дробів

Із двох дробів з однаковими знаменниками той дріб більший у якого більший чисельник.

Приклад. , так як 5>3.

Із двох дробів з однаковими чисельниками той дріб більший, в якого знаменник менший.

Приклад. , оскільки .

 В загальному випадку дроби порівнюються так: множать чисельник першого дробу на знаменник другого, а знаменник першого на чисельник другого. Якщо перший із цих добутків більший (рівний або менший) другого, означає, що перший дріб відповідно більший (рівний або менший) за другий.

 Приклади:  а.  так як ;

б.  =, так як ;

в.  так як .

В деяких випадках співвідношення між дробами легше встановити шляхом порівняння їх з одиницею або половиною.

 

1.2. Арифметичні дії над звичайними дробами

 Додавання. Сумою дробів з однаковими знаменниками називають дріб, що має той же знаменник, а чисельник рівний сумі чисельників даних дробів, тобто:

.

Це означення можна сформулювати також у вигляді наступного|такого| правила.

Щоб додати дроби з однаковими знаменниками, треба додати їх чисельники, а знаменник залишити той же.

Приклад. .

Щоб додати дроби з різними знаменниками, треба привести їх до найменшого спільного знаменника, а потім додати отримані чисельники і під сумою підписати спільний знаменник.

Приклад. .

Коротше записують так: .

Щоб додати мішані числа, потрібно окремо додати їхні цілі та дробові частини.

Приклад. .

Віднімання. Віднімання дробів можна визначити як дію, зворотну додаванню дробів. Відняти від| одного дробового числа друге – означає знайти третє число, яке в сумі з другим дає перше. Із цього означення слідує правило:

Щоб відняти дроби з однаковими знаменниками, потрібно відняти від чисельника зменшуваного чисельник від’ємника, знаменник залишити той же.

Приклад.

Щоб відняти дроби з різними знаменниками, потрібно спочатку привести їх до найменшого спільного знаменника, потім від чисельника зменшуваного відняти чисельник від'ємника і під їх різницею підписати спільний знаменник.

Приклад.

Щоб відняти два мішаних числа, треба від цілої і дробової частини зменшуваного відняти відповідно цілу і дробову частину від’ємника.

Приклад. .

Якщо ж дріб від'ємника більший за дріб зменшуваного, то беруть одну одиницю з цілої частини зменшуваного, роздрібнюють її на долі і додають до дробу зменшуваного, після чого роблять, як описано вище.

Приклад. .

                                             Аналогічно роблять, коли треба відняти з|із| цілого числа дріб.

 

1.3. Властивості додавання і віднімання дробових чисел.

Всі закони і властивості додавання і віднімання натуральних чисел справедливі і для дробових чисел. Їх застосування в багатьох випадках значно спрощує процес обчислення.

Множення. Щоб помножити дріб на дріб, потрібно помножити чисельник на чисельник,а знаменник на знаменник, перший добуток зробити чисельником, а другий - знаменником:

.

При множенні необхідно виконувати  скорочення, по можливості.

Приклад. .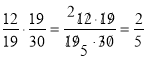

Якщо враховувати, що ціле число є дробом зі знаменником 1, то множення дробу на ціле число і цілого числа на дріб можна виконати за цим же правилом.

Приклад. .

Множення мішаних чисел. Щоб перемножити мішані числа, потрібно заздалегідь перетворити|звернути| їх в неправильні дроби, потім перемножити за правилом множення дробів.

Приклад.

Якщо ж мішане число помножити на ціле, то простіше множити окремо цілу і дробову частини.

Приклад. .

Закони і правила множення натуральних чисел справедливі і для дробів. Їх використання спрощує усні і письмові обчислення.

Приклади.

1. .

2.  .

3.  .

4. .

 

 Ділення дробів. Щоб розділити дріб на дріб, потрібно чисельник першого дробу помножити на знаменник другого, а знаменник першого на чисельник другого і перший добуток записати чисельником, а другий — знаменником:

.

Приклад. .

За цим же правилом можна виконувати ділення дробу на ціле число і цілого

на дріб, якщо представити ціле число у вигляді дробу зі знаменником 1.

Приклади.

          1. ;

          2. .

Проте в останньому прикладі простіше чисельник розділити на ціле число:

.

Ділення мішаних чисел. Щоб виконати  ділення мішаних чисел, їх заздалегідь перетворюють в неправильний дріб, а  потім ділять за правилом ділення дробів.

Приклад. .

Проте при діленні мішаного числа на ціле інколи буває зручніше ділити окремо цілу і дробову частини мішаного числа.

Приклад. .

Враховуючи це, можна ділення виконувати за наступним правилом.

Щоб розділити одне число на інше, потрібне ділене помножити на число, обернене дільнику.

Приклад. .

 

1.4. Основні типи задач на дроби.

Знаходження дробу від числа. Існує багато задач, в яких потрібно знайти частину або дріб від даного числа. Такі задачі розв’язують множенням.

Задача. Господарка мала 20 грн.; їх вона витратила на покупки. Скільки господарка витратила на покупки?

Потрібно знайти числа 20. Зробити це можна так: .

Відповідь. Господарка витратила 8 грн.

В цій задачі: 20 – дане число, – дріб, виражений шуканою частиною, 8 – шукана частина даного числа.

Приклади.

            1. Знайти від 30.       Розв’язок .  

            2. Знайти   від .  Розв’язок .

 

Щоб знайти дріб від даного числа, потрібно дане число помножити на цей дріб.

  Знаходження числа за відомою його частиною. Іноді потрібно за відомою частиною числа і дробу, яка виражає цю частину, визначити це число. Такі задачі розв’язуються діленням.

Задача. В класі 12 комсомольців, що складає частини всіх учнів класу. Скільки всіх учнів в класі? .       Відповідь. 20 учнів.

Приклад. Знайти число, яке складає 34. .

Щоб знайти число за відомою його частиною, потрібно поділити цю частину на даний дріб.

  Знаходження відношення двох чисел. Задача. Робочий виготовляє за день 40 деталей. Яку частину місячного завдання виконав робочий, якщо місячний план складає 400 деталей?

 .      Відповідь. Робочий виконав частину місячного плану.

 

1.5. Завдання для практичних навичок

Приклади:

1. Обчислити:   6.   Обчислити :

2.  Обчислити:   7. Обчислити:

3. Обчислити:   8. Обчислити:

4.  Обчислити:                9. Обчислити:

 5.  Обчислити :    10.  Обчислити:

11.  Обчислити:   22.  Обчислити:

12.  Обчислити:   23. Обчислити:

13. Обчислити:  24.  Обчислити: .

14. Обчислити:   25.  Обчислити:

15. Обчислити:   26.  Обчислити:

16.  Обчислити:   27.  Обчислити:

17.  Обчислити:                 28.  Обчислити :

18.  Обчислити :                 29.  Обчислити :

19.  Обчислити :  30.   Обчислити : 

20.  Обчислити:   31.  Обчислити:  

21.  Обчислити:                    32.  Обчислити:

33.  Обчислити: .