Тест «Деякі функції та їх графіки»
Однією з умов засвоєння програмового матеріалу є міцне засвоєння теоретичного матеріалу. Важливо привчати учнів систематично працювати з підручником, не тільки виконуючи практичні вправи, а й засвоюючи теоретичний матеріал. Пропоную даний тест для перевірки засвоєння теоретичних знань для учнів 11класу на повторення по темі «Деякі функції та їх графіки». Тест має чотири варіанти відповіді, із яких лише одна правильна . Учню пропонується із вказаних варіантів відповідей вибрати тільки одну правильну і занести букву, під якою вона стоїть у бланку відповідей .
Тест з теми «Деякі функції та їх графіки»
- Оберненою пропорційністю називають функцію виду
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Областю визначення функції
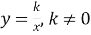
|
А |
Б |
В |
Г |
|
всі числа, крім 0 |
всі числа |
всі додатні числа |
всі цілі числа |
-
Область значень функції
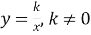
|
А |
Б |
В |
Г |
|
всі недодатні числа |
всі цілі числа |
всі числа |
всі числа, крім 0 |
- Вказати неправильне висловлення.
|
А |
Б |
В |
Г |
|
графіком функції |
графіком прямої пропорційності є пряма, яка проходить через точку (0;0) |
графік функції
|
графіком функції |
-
В якій чверті знаходиться графік функції
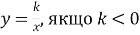 :
:
|
А |
Б |
В |
Г |
|
I та III |
II та IY |
I та Y |
II таIII |
-
Вказати нулі функції
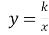 ,
,
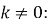
|
А |
Б |
В |
Г |
|
|
|
|
не існує |
- Функція -
|
А |
Б |
В |
Г |
|
це правило, за допомогою якого за кожним значенням залежної змінної можна знайти значення незалежної змінної |
це правило, за допомогою якого за кожним значенням незалежної змінної можна знайти безліч значень залежної змінної |
це правило, за допомогою якого за кожним значенням незалежної змінної можна знайти єдине значення залежної змінної |
це правило, за допомогою якого за деякими значеннями незалежної змінної можна знайти або не знайти значення залежної змінної |
- Незалежну змінну називають
|
А |
Б |
В |
Г |
|
функцією |
аргументом функції |
значенням функції |
степенем числа |
- Вказати неправильне висловлення.
|
А |
Б |
В |
Г |
|
усі значення, яких набуває аргумент, утворюють область визначення функції |
усі значення, яких набуває залежна змінна, утворюють область значень функції |
значення залежної змінної називають значенням функції |
усі значення, яких набуває незалежна змінна, утворюють область значень функції |
-
Що означає запис
 ?
?
|
А |
Б |
В |
Г |
|
аргументу |
|
|
аргументу |
- Функція вважається заданою,
|
А |
Б |
В |
Г |
|
якщо вказана область визначення |
якщо вказана область визначення і правило, за допомогою якого можна за кожним значенням незалежної змінної знайти значення залежної змінної |
якщо вказана область визначення і правило, за допомогою якого можна за кожним значенням залежної змінної знайти значення незалежної змінної |
якщо вказана область значення |
- Яка з фігур не є графіком функції
|
А |
Б |
В |
Г |
|
пряма |
точка |
півколо |
коло |
- Скільки спільних точок може мати з графіком функції будь-яка пряма, перпендикулярна до осі абсцис?
|
А |
Б |
В |
Г |
|
жодної |
безліч |
одну |
три |
-
Графік функції
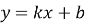
|
А |
Б |
В |
Г |
|
утворює з додатним напрямом осі абсцис гострий кут, якщо |
утворює з додатним напрямом осі абсцис тупий кут, якщо |
cпівпадає з віссю абсцис, якщо
|
паралельний осі абсцис, якщо
|
- Лінійною функцією називають функцію, яку можна задати формулою
|
А |
Б |
В |
Г |
|
|
|
|
|
- Графіком прямої пропорційностіє
|
А |
Б |
В |
Г |
|
пряма з ко-ефіцієнтом |
пряма, паралель-на осі абсцис |
пряма, паралельна осі ординат |
пряма, яка проходить через точку (0;0) |
- Вісь абсцис є графіком функції
|
А |
Б |
В |
Г |
|
|
|
|
|
- Вісь ординат є графіком функції
|
А |
Б |
В |
Г |
|
|
|
|
такої функції не існує |
-
В якій точці графік функції
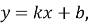
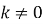
|
А |
Б |
В |
Г |
|
|
|
|
|
-
Графіком функції
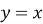
|
А |
Б |
В |
Г |
|
пряма, яка проходить через точку (0;0) |
пряма, яка є бісектрисою 1 та 3 координатних чвертей |
пряма, яка є бісектрисою 2 та 4 координатних чвертей |
пряма, яка паралельна осі ординат |


про публікацію авторської розробки
Додати розробку