Урок "Підсумковий урок з математики в 10-му класі"
Підсумковий урок в 10 класі в кінці навчального року у вигляді гри. Про важливість дидактичної гри свідчать результати навчання, на їх користь висловлюються педагоги та вчені. Визначний німецький вчений Т. Лейбніц вважав, що винахідливість і дотепність виявляються саме в іграх, а тому заслуговують на повагу. Гра підвищує активність учнів, загострює пам'ять, сприяє вихованню волі, наполегливості. Ігри проводяться не заради розваги, а для досягнення певних навчальних цілей. Під час гри виховується почуття колективізму і відповідальності.
Підсумковий урок з математики в 10-му класі
Мета: Повторити матеріал 10 класу з алгебри та геометрії, навчити аналізуватиі узагальнювати, систематизувати знання учнів в нестандартних умовах, розвивати оперативність мислення. Виховувати почуття відповідальності як результат колективної діяльності. Розвивати інтелект, творчі здібності учнів, враховувати інтерес до вивчення математики.
Тип уроку: узагальнення та систематизація знань, умінь.
«Математика – дивовижна вчителька в мистецтві спрямовувати думки, наводити порядок там, де вони невпорядковані, і викорчовувати безглуздя, фільтрувати брудне і наводити ясність.»
Ж. Фабр
Хід уроку
Учитель: Урок сьогодні незвичайний. Його мета – повторити матеріал 10 класу з алгебри та геометрії, удосконалити вміння та навички розв’язування задач з геометрії та алгебри. У встановленому шляхом жеребкування порядку кожна команда обирає категорію, що висвітлена на дошці і по черзі кожен член команди дає відповіді на питання. За правильну відповідь – 1 бал.
І. Перпендикулярність прямих і площин
1) Означення прямої, перпендикулярної до площини.
2) Ознака перпендикулярності прямої і площини.
3) Властивості перпендикуляра і похилої.
4) Теорема про 3 перпендикуляра.
5) Як Микола Іванович Лобачевський прославив своє ім’я?
ІІ. Паралельність прямих і площин у просторі.
- Ознака паралельності прямої і площини.
- Ознака паралельності площин.
- Які властивості фігур не зберігаються при паралельному проектуванні.
- Якою фігурою може бути при паралельному проектуванні проекція чотирикутника, паралелограма, трапеції.
- Головна праця давньогрецького вченого Евкліда, яка побачила світ близько 300 р. до н.е.
ІІІ. Взаємне розміщення площин, прямих у просторі.
- Як у просторі визначають кут між прямими, що перетинаються.
- Які прямі називаються мимобіжними.
- Що таке кут між мимобіжними прямими.
- Дайте визначення кута між прямою і площиною.
- Дайте означення кута між площинами.
ІV. Ірраціональні рівняння. Степенева функція.
- Яке рівняння називається ірраціональним.
- Дайте означення арифметичного кореня n-ного степеня.
- Які радикали називаються подібними.
-
Чи правильно, що
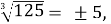 обґрунтувати.
обґрунтувати.
-
Що більше
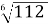 чи
чи 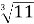 , обґрунтувати.
, обґрунтувати.
V. Тригонометричні функції.
1) Сформулювати означення синуса довільного числа.
2) Знайти найменший період функції ![]() .
.
3) Формула суми косинусів, синусів, тангенсів.
4) Загальна формула розв’язку рівняння ![]() ,
, ![]() ,
, ![]()
![]()
5) Які рівняння називаються тригонометричними.
Після І конкурсу підводяться підсумки. За уточнення інші команди можуть отримати додаткові бали.
ІІ конкурс – презентація «Розміщення основи перпендикуляра, проведеного з точки простору, яка рівновіддалена від вершин та сторін фігури».
Учні представляють презентації і обґрунтовують місце знаходження основи перпендикуляра, пояснюють елементи побудови паралельних проекцій з урахуванням властивостей паралельного проектування, вказують радіуси описаних та вписаних кіл.
Представники інших команд задають додаткові запитання:
- Формула радіуса описаного rола навколо трикутника;
- Формула радіуса описаного кола навколо правильного трикутника;
- Формула радіуса вписаного кола в правильний n-кутник;
- Формула радіуса кола вписаного в трикутник;
- За якої умови навколо 4-кутника можна описати коло;
- Чи навколо будь-якої трапеції можна описати коло;
- В який чотирикутник можна вписати коло?
Презентація оцінюється в 5 балів. В оцінюванні приймає участь учитель інформатики. За кожну правильну відповідь на додаткове питання команда отримує 1 бал.
По завершенні конкурсу підводяться підсумки.
ІІІ конкурс. Завдання на встановлення відповідності.
До кожного завдання в двох колонках подано інформацію, яку позначено цифрами (1-4) і буквами (А-D). Виконувати завдання необхідно встановлюючи відповідність інформації, позначеної цифрами і буквами(утворити логічні пари).
- Встановити відповідність:
-
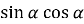 А.
А. 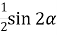
-
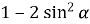 Б.
Б. 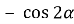
-
 В.
В. 
-
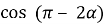 Г.
Г. 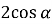
Д. ![]()
- Встановити відповідність.
-
 А. Ø
А. Ø
-
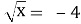 Б. -4;4.
Б. -4;4.
-
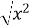 = 16. В. 16.
= 16. В. 16.
-
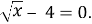 Г. -16.
Г. -16.
Д. -16;16.
- Встановити відповідність.
-
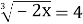 А. Ø
А. Ø
-
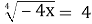 Б. - 64.
Б. - 64.
-
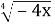 = - 4. В. - 32.
= - 4. В. - 32.
-
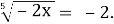 Г. 32.
Г. 32.
Д. 16.
-
SO
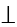
-
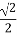 . Відстань від S до вершини А. А. 4
. Відстань від S до вершини А. А. 4
-
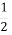 Відстань від О до А. Б. 1.
Відстань від О до А. Б. 1.
-
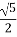 . Відстань від О до АВ. В. 2
. Відстань від О до АВ. В. 2
-
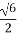 . Відстань від B до вершини D. Г.
. Відстань від B до вершини D. Г. 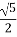
- Відстань від S΄ до AD.
- Із центра правильного трикутника АВС проведено перпендикуляр SO = 1 см. Сторона трикутника АВ = 1 см. Встановити відповідність між заданими відстанями та числовими значеннями.
-
Відстань від т.О до т.А. А.
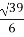
-
Відстань від О до АВ. Б.
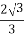
-
Відстань від S до АВ. В.
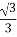
-
Відстань від S до вершини А. Г.
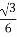
Д. ![]()
6. Встановити відповідності між кутами нахилу відрізка довжиною 10 см до площини та довжиною його проекції на площину.
1) 30˚; А. 5см.
2) 45˚; Б. 5![]() см.
см.
3) 60˚; В. 5![]() см.
см.
4) 0. Г. 0 см.
Д. 10 см.
Підсумок
Вчителі підводять підсумок уроку, визначаючи переможців, оцінюють та надають слово представникам команд, які висловлюють думку щодо ходу уроку.
Учитель закінчує урок словами Олексія Миколайовича Крилова: «Рано чи пізно будь-яка правильна математична ідея знаходить застосування в тій чи іншій справі. Завтра математика стане ще могутнішою, ще важливішою і потрібнішою, ніж сьогодні».


про публікацію авторської розробки
Додати розробку
