Тест "Паралелепіпед.Призма"

Тестові завдання « Паралелепіпед. Призма»

1. Прямокутним паралелепіпедом називають  …

А) паралелепіпед, основою якого є прямокутник;  Б) паралелепіпед, протилежні грані якого паралельні;  В) прямий паралелепіпед, основою якого є прямокутник; Г) паралелепіпед, основою якого є паралелограм Д) паралелепіпед, діагоналі якого рівні і перпендикулярні.

2. Діагоналі паралелепіпеда перетинаються в одній точці і …

А) рівні;  Б) точкою перетину діляться навпіл.   В) їх чотири; Г) перпендикулярні;

Д) мають різну довжину.

3. Вимірами прямокутного паралелепіпеда  є …

А) довжина, ширина, висота; Б) довжини непаралельних ребер; В) довжина і висота  Г) довжини паралельних ребер. Д) діагоналі паралелепіпеда

4. Виміри прямокутного паралелепіпеда: 3 см, 4 см і 5 см, а діагональ дорівнює …

А) 10 см;  Б) 60 см;  В) 12 см;   Г) 5 см;   Д) 2 см.

5. Якщо ребро куба дорівнює 3 см, то площа його поверхні дорівнює …

А) 9 см²;  Б) 36 см²;  В) 54 см²;  Г) 27 см²;  Д) 3 см².

6. Виміри прямокутного паралелепіпеда дорівнюють 4 см, 1 см і 5 см. Знайти площу його повної поверхні.

А) 20 см²; Б) 29 см²; В) 58 см²; Г) 48 см²; Д) 40 см².

7. Сума довжин усіх бічних ребер прямокутного паралелепіпеда дорівнює 120 см. Визначте довжину його висоти.

А) 15 см;    Б)  30 см;   В) 40 см;   Г) 60 см;   Д) 10 см

8. В основі прямої призми лежить рівнобічна трапеція з основами 4 і 6 см та бічною стороною 5 см. Бічне ребро призми дорівнює 10 см. Обчислити бічну поверхню цієї призми.

А)150 см² ;  Б) 200   см² ;     В)100 см²;  Г)  50 см² ; Д)  300 см²

9. Радіус кола, вписаного в основу правильної трикутної призми, дорівнює 2√3 см. Бічне ребро цієї призми дорівнює 10 см. Обчислити бічну поверхню призми.

А)  240  см²;   Б)60√3  см²;    В)  180 см²;     Г) 360  см²;  Д)  120 см²

10

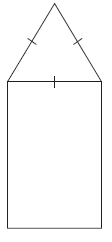11. На рисунку зображено прямокутник і трикутник, що є гранями правильної трикутної призми. Периметр цього прямокутника дорівнює 38 см. Визначте площу основи цієї призми, якщо довжина висоти призми дорівнює 11 см.

      А) 16√3 см²;  Б)   32√3  см²;  В)  24 см² ;    Г) 64  см²;    Д) 24√3  см²

12