Тести. Функція та її властивості. Квадратична функція. Геометричні перетворення функції.

Тести № 4

Функція та її властивості. Квадратична функція. Геометричні перетворення функції

1. Функцією називається

а) називають залежність між змінними x та y, при якій кожному значенню x відповідає єдине значення змінної y

б)  називають залежність між змінними x та y

в) відповідність між двома змінними

г)  відповідність між абсцисою та ординатою

2. Змінна х називається

а) ординатою

б) функцією

в) аргументом

г) залежною змінною

3. Змінна у називається

а) абсцисою

б) незалежною змінною

г) аргументом

в) ординатою

4. Областю визначення функції називається

а) множина допустимих значень аргументу функції

б) множина допустимих значень ординати функції

в) множина допустимих залежних значень функції

г) множина допустимих значень у функції

5. Областю значень функції називається

а) множина допустимих значень аргументу функції

б) множина допустимих значень ординати функції

в) множина допустимих незалежних значень функції

в) множина допустимих значень абсциси функції

6. Нулями функції називають значення 

а) аргументу, при яких функція набуває значення нуль

б) ординати, при якому абсциса набуває значення нуль

в) залежної змінної, при якому аргумент набуває значення нуль

г) аргументу, при яких абсциса набуває значення нуль

7. Квадратичною функцією називають функцію, яку можна задати у вигляді 

а) y=ax²+bx+c, де a,b,c — дійсні числа, при чому a≠0

б) y=ax³+bx+c, де a,b,c — дійсні числа, при чому a≠0

в) y=ax+b, де a,b — дійсні числа, при чому a≠0

г) , де к – дійсне число, при чому х 0.

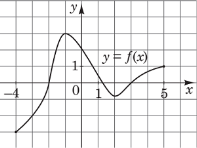
8. Область визначення функції  на

а) (-3; 3)   б) (-4; 5)  в)   г)

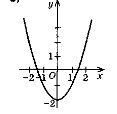9. Координати вершини параболи

а) (2; 0)

б) (0; 2)

в) (0; -2)

г) (-2; 0)

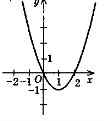
10. Координати вершини параболи

а) (0; 0)

б) (2; 0)

в) (1; -1)

г) (-1; 1)

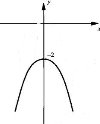
11. Функція на малюнку задана формулою

а) у = х² -2

б) у = (х – 2)²

в) у = - (х – 2)²

г) у = - х² -2

12. Функція на малюнку задана формулою

а) у = (х – 1)² + 1

б) у = - (х – 1)² - 1

в) у = (х + 1)² + 1

г) у = (х – 1)² - 1