9-кл.Алгебра.Презентація:,, Квадратична функція її графік і властивості.''
Про матеріал
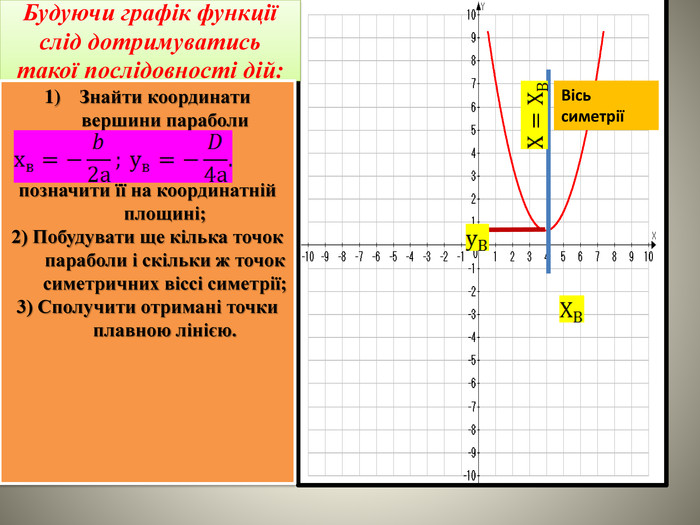
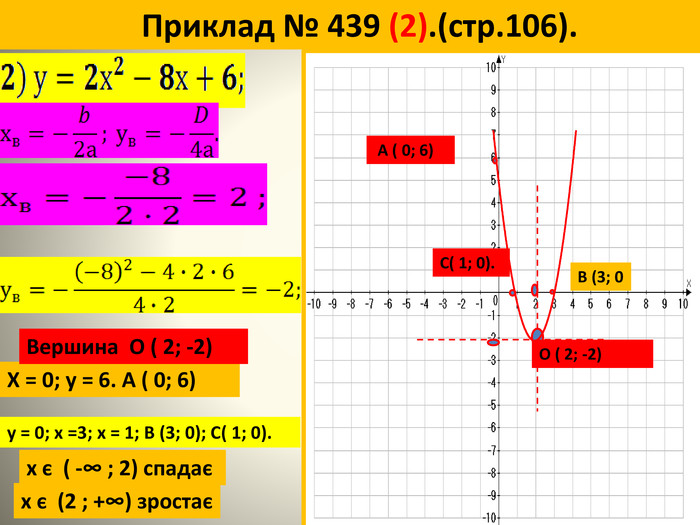
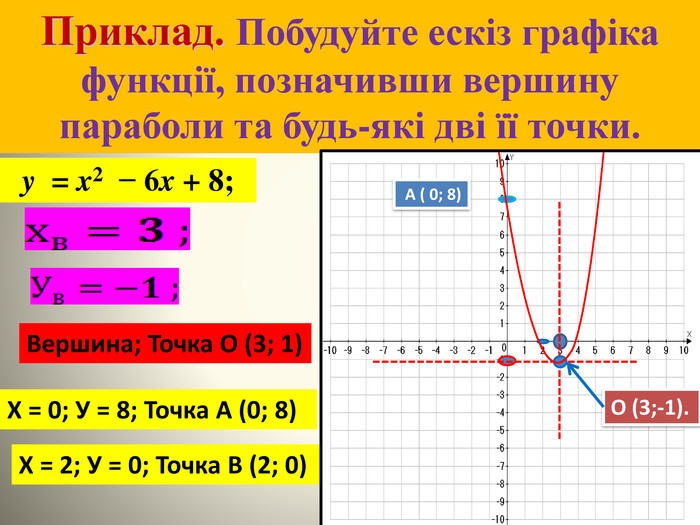
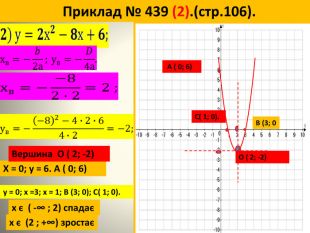
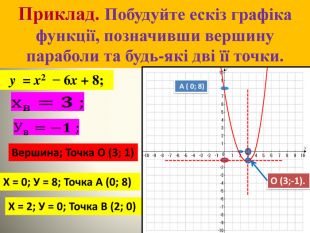
В даній роботі введені означення квадратичної функції виведена формула для знаходження вершини параболи.Показані побудови графіків за визначеним алгоритмом.Схеми основних видів перетворення. Перегляд файлу
Зміст слайдів
pptx
До підручника
Алгебра 9 клас (Істер О. С.)
До уроку
§ 11. Функція y = ax2 + bx + c, a ≠ 0, її графік і властивості Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку