Тестові завдання тригонометричні співвідношення прямокутного тркутника
Тестові завдання
Варіант 1
- (0,5 бала) Яке з наведених тверджень правильне?
А Косинусом гострого кута називається відношення протилежного катета до прилеглого
Б Косинусом гострого кута називається відношення прилеглого катета до гіпотенузи
В Косинусом гострого кута називається відношення протилежного катета до гіпотенузи
Г Косинусом гострого кута називається відношення прилеглого катета до протилежного
- (0,5 бала) У прямокутного трикутника ABC один із катетів дорівнює 8 см, а синус протилежного кута – 0,2. Знайдіть гіпотенузу.
А 0,4 см
Б 40 см
В 1,6 см
Г 8,2 см
- (0,5 бала) Катети прямокутного трикутника дорівнюють 4 см і 5 см. Знайдіть гіпотенузу.
А ![]()
Б 3 см
В 9 см
Г 1 см
- (0,5 бала) Яке з наведених тверджень неправильне?
А У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів
Б Гіпотенуза прямокутного трикутника більша за кожен із його катетів
В Із двох похилих більша та, у якої проекція більша
Г Катет дорівнює добутку гіпотенузи на синус кута, протилежного цьому катету
- (0,5 бала) Чому дорівнює cos60?
А ![]()
Б ![]()
В 1
Г ![]()
-
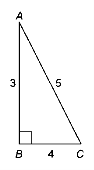
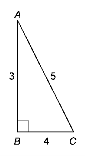
(0,5 бала) На якому з наведених рисунків sinA
 ?
?
|
А |
|
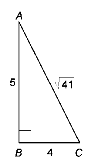
В |
|
|
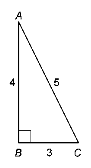
Б |
|
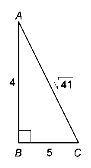
Г |
|
- (1 бал) Сторони прямокутника дорівнюють 12 см і 16 см. Знайдіть довжину діагоналей прямокутника.
А ![]()
Б 20 см
В ![]()
Г 40 см
- (1 бал) Бічна сторона рівнобедреного трикутника дорівнює 29 см, а його висота, що проведена до основи, – 21 см. Знайдіть основу трикутника.
А 20 см
Б 40 см
В 30 см
Г 26 см
- (1 бал) У рівнобічній трапеції бічна сторона дорівнює 25 см, висота трапеції – 7 см. Знайдіть тангенс гострого кута трапеції.
А ![]()
Б ![]()
В ![]()
Г ![]()
Варіант 2
- (0,5 бала) Яке з наведених тверджень правильне?
А Котангенсом гострого кута називається відношення протилежного катета до прилеглого
Б Котангенсом гострого кута називається відношення прилеглого катета до гіпотенузи
В Котангенсом гострого кута називається відношення протилежного катета до гіпотенузи
Г Котангенсом гострого кута називається відношення прилеглого катета до протилежного
- (0,5 бала) У прямокутному трикутнику ABC гіпотенуза дорівнює 8 см, а синус гострого кута – 0,2. Знайдіть катет, протилежний даному гострому куту.
А 0,4 см
Б 40 см
В 1,6 см
Г 5 см
- (0,5 бала) Із точки, що розташована поза прямою, проведено до цієї прямої перпендикуляр довжиною 6 см і похилу довжиною 10 см. Чому дорівнює довжина її проекції на пряму?
А ![]()
Б 8 см
В 9 см
Г 4 см
- (0,5 бала) Яке з наведених тверджень неправильне?
А У прямокутному трикутнику квадрат гіпотенузи дорівнює сумі квадратів катетів
Б Трикутник, сторони якого дорівнюють 3, 4 і 5, називають єгипетським
В Із будь-якої точки площини, що не лежить на даній прямій, можна провести два перпендикуляри до цієї прямої
Г Катет дорівнює добутку гіпотенузи на синус кута, протилежного цьому катету.
- (0,5 бала) Чому дорівнює sin30?
А ![]()
Б ![]()
В 1
Г ![]()
-
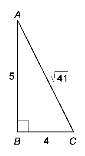
(0,5 бала) На якому з наведених рисунків tgA
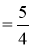 ?
?
|
А |
|
В |
|
|
Б |
|
Г |
|
- (1 бал) Сторони прямокутника дорівнюють 12 см і 5 см. Знайдіть довжини діагоналей прямокутника.
А ![]()
Б 13 см
В ![]()
Г 26 см
- (1 бал) Бічна сторона рівнобедреного трикутника дорівнює 17 см, а його висота, що проведена до основи, – 8 см. Знайдіть основу трикутника.
А 30 см
Б 15 см
В 20 см
Г 24 см
- (1 бал) Висота рівностороннього трикутника дорівнює 5 см. Чому дорівнює його сторона?
А ![]()
Б ![]()
В ![]()
Г 10


про публікацію авторської розробки
Додати розробку