ЗАСТОСУВАННЯ ПОХІДНОЇ ДО РОЗВ'ЯЗУВАННЯ ПРИКЛАДНИХ ЗАДАЧ. Урок- телеміст

ЗАСТОСУВАННЯ ПОХІДНОЇ ДО РОЗВ'ЯЗУВАННЯ ПРИКЛАДНИХ ЗАДАЧ

Математика цікава тоді, коли дає                 

поживу нашій винахідливості до

міркувань.

Д. Пойа

Загальноосвітня мета:

1)   перевірити сформованість умінь:

•    встановлювати характер зміни функції за знаком похідної;

•    виявляти точки, підозрілі на екстремум;

•    використовувати  поняття  похідної для дослі­дження властивостей функції;

2)   встановити, чи можуть учні:

•    застосовувати метод диференціального числення до розв'язування прикладних задач;

•    виділяти етапи в розв'язуванні прикладних задач.

Розвиваюча мета: розвивати пізнавальний інтерес, навички колективної праці, вміння використовува­ти сформовані знання, навички й уміння в нових ситуаціях; формувати навички взаємоконтролю та самоконтролю.

Виховна мета: виховувати працьовитість, охайність ведення записів, вміння об'єктивно оцінювати ре­зультати індивідуальної і колективної роботи; при­щеплювати бажання мати якісні, глибокі знання, доводити почату роботу до кінця; виховувати зібраність, організованість, увагу, відповідальність, вимогливість до себе.

Типу уроку: урок-телеміст.

Примітка. Учні готуються до уроку вдома за 6-8 днів. Клас поділяється на команди і в кожній обирається ведучий. Команди готують привітання, з якими вступають на початку телемосту. Вчитель спочатку роздає ведучим картки-завдання, які вони виконували вдома.

Питання, що обговорюються на уроці:

1.   Похідна - фундаментальне поняття математики.

2.   Похідна - засіб дослідження процесів дійсності та сучасного виробництва.

ХІД УРОКУ

I етап уроку. Організаційний момент

II етап уроку. Вступне слово вчителя. Історичні відомості

Похідна - одне з фундаментальних понять математики.

Відкриттю похідної і основ диференційного числен­ня передували роботи французького математика і юриста П'єра Ферма (1601 - 1665), який у 1629 р. запропонував способи знаходження найбільших і найменших значень функцій, проведення дотич­них до довільних кривих, що фактично спиралися на застосування похідних. Цьому сприяли також ро­боти Рене Декарта (1596-1650), який розробив ме­тод координат і основи аналітичної геометрії. Лише в 1666 р. англійський математик і механік І. Ньютон (1643-1727) і дещо пізніше видатний німецький філософ і математик Готфрід Вільгельм Лейбніц (1646-1716) незалежно один від одного побудували теорію диференціального числення. І. Ньютон дійшов поняття похідної, розв'язуючи задачі про миттєву швидкість, а Лейбніц, - розглядаючи гео­метричну задачу про проведення дотичної до кри­вої. Термін "похідна" ввів у 1797 р. французький ма­тематик Жозеф Луї Лагранж (1736-1813). Він увів і сучасні позначення для похідної у вигляді у' та f'. Сам термін "похідна" є буквальним перекладом відповідного французького слова derivee, яке досить влучно пояснює зміст цього поняття: функція f '(x) у певному розумінні походить від функції f (x), тоб­то є похідною від неї. До Лагранжа похідну за про­позицією Лейбніца називали диференціальним коефіцієнтом і позначали . Позначення Лейбніца виявилось дуже вдалим, оскільки чітко відображало саме походження похідної - як границі відношення . Тому його часто використовують і в сучасних курсах аналізу. Ньютон, який у своїх підходах до обґрунтування математичного аналізу широко за­стосовував фізичні уявлення, похідну називав флексією (дослівно з латини - "витіканням"), а саму функцію флюєнтною (дослівно "текучістю"). Ці терміни Ньютона не прищепилися.

Терміни "диференціальний", "диференційована", "диференціювання" тощо, які тією чи іншою мірою пов'язані з поняттям похідної, відображають той суттєвий аспект утворення поняття похідної, який пов'язаний зі знаходженням різниці

та х-х₀ =∆х

(слово differentia в перекладі з латини означає "різниця").

Велику роль у розвитку диференціального числення відіграв Л. Ейлер, який написав підручник "Дифе­ренціальне числення" (1755).

За допомогою диференціального числення було розв'язано цілий ряд задач теоретичної механіки, фізики та астрономії. Зокрема, використовуючи ме­тоди диференціального числення, вчені передбачи­ли повернення комети Галлея, що стало тріумфом науки XVIII ст.

За допомогою цих самих методів математики у XVIII ст. вивчали різні криві: знайшли криву, по якій швидше за все падає матеріальна точка; навчи­лись знаходити кривину ліній.

І сьогодні поняття похідної знаходить широке за­стосування в різних областях науки та техніки.

Ill етап уроку. Повідомлення теми та мети уроку. Постановка проблеми

Ведучі команди пропонують обговорити актуальні проблеми.

Ведучий першої команди. Нашій творчій групі доручено з'ясувати, яким повинен бути кут прилягання під'їзного шляху до магістралі, щоб су­марний річний пробіг автомобілів з одного пункту до двох інших був найменший.

Ведучий другої команди. Наша група пра­цює над спорудженням зрошувального каналу, який має форму рівнобічної трапеції. Треба з'ясувати, при якому куті нахилу бічних сторін, переріз зрошу­вального каналу буде мати максимальну площу?

Ведучий третьої команди. Наша проблема полягає в наступному: знайти найбільш економічну швидкість океанського танкера.

Ведучий четвертої команди. Наша творча група розраховує розмір консервної банки заданого об'єму, за умови, що на її виготовлення, витра­чається найменша кількість жесті.

IV етап уроку. Телерозминка: актуалізація опорних знань з теми "Похідна та її застосу­вання"

Учням пропонуються запитання:

1.   Як пов'язані між собою монотонність функції та їх похідна?

2.   Що відбувається з похідною в точці її екстремуму?

3.   В яких точках неперервні функції:

а)   многочленР(х) = а₀хⁿ + а₁х^n-1 +..■+а_п-1х + а_п;

б)  дробово-раціональна?

Відповідь, а) Многочлен неперервний на всій число­вій прямій;

б)  дробово-раціональна функція неперервна в усіх точках своєї області визначення.

4.   Вказати проміжки неперервності функції:

a) f(х) = х²-4;

б)

в)  f(х)= -2х + 7;

г)  ;

Д)

е).

Відповідь, a) R; б) (-∞; 3) і (3; +∞); в) R; г) R; д)(- ∞; 2); (2; 5) і(5; ₊∞)_;е)(- ∞; 7),(7; +∞).

5.  З якої кількості неперервних "шматків" склада­ються графіки функцій?

a) ;

б)

в)

Відповідь, а) Із двох; б) з трьох; в) з чотирьох.

6.  Який кут (гострий або тупий) утворює з додатним напрямком осі Ох дотична до графіка функції?

а) у = х⁴ -2, у точках 1, 2, - 1;

б)   у = х³ -х^г, у точках 1, - 1, 0;

в)   у = (х-2) , у точках 0, 4, - 3.

Відповідь, а) Гострий, гострий, тупий; б) гострий, гострий, 0°; в) тупий, гострий, тупий.

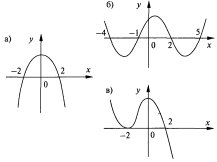
7. При яких значеннях змінної х функції, графіки похідних яких зображені на рисунку, мають точки максимуму і мінімуму? Назвіть ці точки.

Відповідь, а) х=-2 - точка мінімуму, х=2 - точка максимуму; б) х = -1, х=5 - точка мінімуму; х=-4, х=2- точка максимуму; в) х = 2- точка максимуму.

V етап уроку. Обговорення задач прикладного характеру

Для активізації діяльності школярів під час роз­в'язування та наступного обговорення задач кожну команду можна "розбити" на дві підкоманди (з ме­тою обміну задачами). Під час роботи звучить спокійна музика.

Задача 1

З'ясувати, яким повинен бути кут прилягання під'їзного шляху СЕ до магістралі АВ, щоб сумарний річний пробіг автомобілів з С до А та В був якомога меншим. Відомо, що рух між Сі А буде в 3 рази інтенсивніший, ніж між С і В; АВ =100 км; АС = 30 км (див. рис.).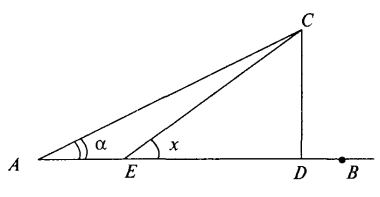

Розв'язання

1-й етап. Моделювання

1.   Нехай п - кількість рейсів, яка планується в се­редньому протягом року з С до В.

2.   Тоді сумарний річний пробіг автотранспорту з С у А та В можна підрахувати так:

S(x) = 2nAC+nCE+nBE = 2n(AE+EC)+n(EC+BE) =2пАЕ + 2пЕС + пЕС + пВЕ = 2пАЕ + ЗпЕС + пВЕ = пАЕ + пАЕ + пВЕ + 3пЕС = 3пЕС + пАВ + пАЕ = п(3ЕС + АВ + AE); S(x)=n(3EC + АВ + АЕ).

3.   З цієї формули видно, що точку прилягання Е не має сенсу вибирати вправо від D, оскільки в цьому випадку СЕ > CD, AE > AD, і тому значення S буде більшим, ніж при Е = D. Тому,

4.   Виразивши з прямокутного трикутника CDE дов­жини сторін СЕ і DE через CD та х, отримаємо:

, де                (1)

Математична задача. Дослідити функцію (1) на найменше значення на заданому відрізку.

2-й етап. Розв'язання в середині математичної моделі

1. ,

                                         ,

,

 

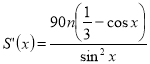х - єдина критична точка функції S( х);

2. S'( х)< 0  при;

3.  S'( х)> 0  при

4.   При х = 70 ° функція S набуває найменшого зна­чення.

3-й етап. Критичне осмислення отриманого результату

Кут прилягання під'їзного шляху до магістралі по­винен наближено дорівнювати 70°.

Відповідь. 70°.

Задача 2

Зрошувальний канал має форму рівнобічної тра­пеції, бічні сторони якої дорівнюють меншій основі. При якому куту нахилу бічних сторін переріз каналу буде мати максимальну площу?

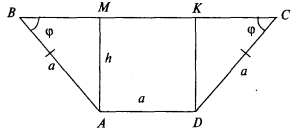
Розв'язання

1-й етап. Моделювання

1.    Розглянемо прямокутний трикутник АВМ:

AM = h = a sinφ, BM =a cosφ.

2.   BM = CK = a cosφ.

3.   BC=a + 2a cosφ.

4.   S(ABCD) =,

S( ABCD) = = = (a (1+cos φ))asin φ = a²sinφ(1+cos φ)

= (a(l + cos φ))a∙sin φ = a² sin φ (l + cos φ).

5.    Ми отримали

F(φ) = а² sinφ (1 +cosφ).                    (1)

Математична задача. Дослідити функцію (1) на найбільше значення.

2-й етап. Розв'язання всередині математичної моделі

1.     F '(φ) = a² ∙(cos φ(1+cos φ)) + sin φ ∙(-sin φ) =

= а²(cos φ + cos ²φ - sin² φ) = a² (cos φ + cos² φ + cos² φ -1) =

= а² (2 cos² φ + cos φ - 1).

2.    F '(φ) = а² (2 cos² φ + cos φ - 1), 2 cos² φ + cos φ – 1 = 0,

3.   Оскільки φ - гострий кут, то , φ=60⁰.

3-й етап. Критичне осмислення отриманого результату

Переріз зрошувального каналу буде мати макси­мальну площу при куті нахилу бічних сторін 60°.

Відповідь. 60°.

Задача З

Витрати на паливо, необхідне для руху океанського танкера, пропорційні кубу його швидкості та скла­дають 20 у. о. За годину при швидкості 10 вузлів (ву­зол дорівнює морській милі за годину), а всі інші витрати складають 100 у. о. за годину. Знайти най­більш економічну швидкість руху за тихої погоди. Обчислити додатковий прибуток, якщо відстань до порту призначення 1000 морських миль (морська миля дорівнює 1852 м).

Розв'язання

1-й етап. Моделювання

Нехай х вузлів - найбільш економічна швидкість океанського лайнера (у. о.) - витрати палива при швидкості х вузлів; (год) – час руху, за який танкер пройде 1000 морських миль.

Складемо функцію витрат коштів за один рейс:

(у. о.).

Враховуючи й інші види витрат, які складають 100 у. о. за годину, отримаємо:

(у. о.).                 (1)

х

Математична задача. Дослідити функцію (1) на найменше значення.

2-й етап. Розв'язання всередині математичної моделі

Треба знайти х(0 < х < +∞), при якому функція P = f(x) набуває найменшого значення.

1) Р' =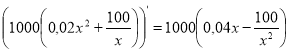

2)  , , 0,04x³ = 100, x =, x = 13,6

,

Отже, 13,6 вузлів є найбільш економічною швид­кістю.

Примітка. Візьмемо до уваги, що коли х→ 0 і х → ∞, то Р → ∞. Це означає, що дуже мала і велика швидкість не дають найменшої суми утримання судна на 1 милю шляху, бо за малої швидкості на одну милю шляху витрачається багато часу, і, отже, підвищується вартість утримання команди. За дуже великої швидкості витрачається багато палива.

3-й етап. Критичне осмислення отриманого результату

Найраціональнішою є швидкість 13,6 вузлів.

4-й етап. Інтерпретація

Обчислимо витрати коштів на 1000 морських миль за швидкості 10 та 13,6 вузлів.

(у. о.);

(у. о.).

Р_{Д. П.} - додатковий прибуток за один рейс у 100 мор­ських миль.

Р_{Д. П.} =P₁ – P₂  Р_д.п. = 12000 – 11030 = 970 у. о.

Відповідь. 13,6 вузлів, 970 у. о.

Задача 4. Визначити розміри циліндричної закритої консервної банки, об'єм якої V см³, щоб її повна по­верхня була найменшою, тобто щоб витрати жесті на її виготовлення були найменшими.

Розв'язання

1-й етап. Моделювання

Позначимо діаметр основи банки через х, висоту че­рез h. Тоді повна поверхня банки виразиться форму­лою:

S = 2 ∙πх² + πxh.

Оскільки об'єм банки V відомий, то, використовую­чи формулу для обчислення об'єму циліндра

, виразимо висоту h через х:.

Подамо функцію S через одну змінну х:

де х >0.

Математична задача. Визначити найменше значен­ня функції S = f( х) на проміжку 0 < х< ∞.

2-й етап. Розв'язування всередині математичної моделі

1) ;

2) S' = 0 , πx³-4V =0,  

Тут не можна порівняти значення функції в кри­тичній точці з її значенням на кінцях проміжку, оскільки проміжок не має правого кінця. Тому тре­ба дослідити знак похідної зліва і справа від критичної точки. Оскільки при х<з/- S'<0, а при

V я

fw

х>\1- S'>0, то повна поверхня зменшується,

V     тс

fw

коли хзростає від 0 до з/-, і зростає, коли хзростає V я

.    fw

ВІД 3/-----ДО+°°.

V   я

Отже, найменшого значення повна поверхня набу-

ш

ває, коли х= зі-. V я

3-й етап. Критичне осмислення отриманого результату

fw

Коли х=з-, то повна поверхня буде найменшою. V  я

При цьому

А = -    ^W

Я?

r_AV\²

У  ^п J

тобто висота дорівнює діаметру основи.

Якщо діаметр і висота банки дорівнюють з/-, то

V я

витрати жесті на її виготовлення будуть наймен­шими. Це означає, що коли осьовий переріз має форму квадрата, то при заданому об'ємі на виготов­лення циліндричної банки витрати жесті будуть мінімальними.

J4V Відповідь, з/-------■ діаметр основи та висоти банки.

V я

Команди учнів подають розв'язки задач, виділяючи при цьому:

1)   математичну модель задачі;

2)   провідну математичну ідею процесу розв'язування;

3)   блок знань, необхідних для розв'язування мате­матичної задачі.

Учитель здійснює остаточне коректування опе­раційної структури навчально-пізнавальних дій.

VI етап уроку. Підсумок уроку

Вчитель і учні підбивають підсумки роботи. Розкри­вається характер помилок, яких припустилися.

Вчитель підбиває підсумок щодо моделювання про­цесів сучасного виробництва. Перш ніж будь-яке явище природи або процес економічного, сільсько­господарського характеру піддавати математичному вивченню, його необхідно спростити. Особливістю розглянутих вище задач є те, що вони мають одну й ту саму математичну модель.

Висновки

1.   Вчитель може вважати, що дії щодо моделюван­ня процесів дійсності повністю сформовано в учнів, якщо вони можуть за умови повної самостійності:

1)   перевести задачу на мову математики;

2)   сконструювати математичну задачу;

3)   виділити провідну математичну ідею;

4)   критично осмислити отриманий результат.

2.   Навчальну дію оцінки можна вважати сформова­ною на цьому етапі, якщо учні:

1)   моделюють процеси дійсності;

2)   знаходять і виправляють помилки у запропонова­них розв'язаннях.