Застосування похідної до розв'язування прикладних задач. (профільний рівень навчання)

 

ТЕМА  УРОКУ: Застосування похідної до розв'язування прикладних задач. (профільний рівень навчання)

 

  Навчальна мета: узагальнити і систематизувати знання, вміння учнів з вивченої теми; ознайомити учнів із різними типами прикладних задач та методами їх розв'язання за допомогою похідної; поглибити знання учнів про моделювання процесів дійсності за допомогою апарата похідної.

 Розвиваюча мета:розвивати зацікавленість математикою; навички колективної праці; вміння використовувати набуті знання; формувати навички взаємоконтролю та самоконтролю

  Виховна мета: виховувати працьовитість , зібраність, організованість, вміння об'єктивно оцінювати результати індивідуальної і колективної праці; прищеплювати бажання удосконалювати та поглиблювати знання, доводити почату роботу до кінця.

   Очікувані результати:

Розв'язування прикладних задач на знаходження найбільших і найменших значень реальних величин. Застосування результатів дослідження функції за допомогою похідної до розв'язування рівнянь і нерівностей, та доведення нерівностей.

   Тип уроку: узагальнення і систематизація знань, умінь, навичок ( урок із використанням методу проектів)

   Обладнання: комп'ютер, роздатковий  матеріал, лінійка, косинець, картки самоконтролю (вчитель підбирає в залежності від вибраних завдань).

                                                             Хід уроку.

І. Організаційний момент

   Учні   сідають по групах, готуючись до проведення уроку ( три групи по чотири учні) Кожен учень одержує картку самоконтролю, де виставляє собі оцінку за участь у кожному етапі уроку.

ІІ. Перевірка домашнього завдання.

Чергові на перерві записали розв'язки домашнього завдання дошці і в ході бесіди було перевірено домашнє завдання.

ІІІ.  Мотивація навчальної діяльності.

ВСТУПНЕ СЛОВО ВЧИТЕЛЯ:

1. З історії диференціального числення. Розділ математики, у якому ви­вчаються похідні та їх застосування до дослідження функцій, називається диференціальним численням. Прирости аргументу ∆х і функції ∆f, які є різницями, відіграють помітну роль у роботі з похідними. Тому природна поява латинського кореня differentia (різниця) у назві calculis differentialis нового числення, яка перекладається як числення різниць; ця назва з'яви­лася вже в кінці XVII ст., тобто під час народження нового методу.

Термін «похідна» є буквальним перекладом на українську французько­го слова derive, яке ввів у 1797 р. Ж. Л а г р а н ж (1736-1813); він же ввів сучасні позначення у', f'. Така назва відображає зміст поняття: функція f ' (х) походить від f(х), є похідною від  f(х).

Диференціальне числення створене порівняно недавно, у кінці XVII ст. Тим дивовижніше, що задовго до цього А р х і м є д (бл. 287-212 рр. до н. є.) не тільки розв'язав задачу на побудову дотичної до такої складної кривої, як спіраль (застосовуючи при цьому граничні переходи), а й зміг знайти максимум функції  f(х)  = х² (а - х).

Розвитку основ диференціального числення сприяли роботи математи­ка і юриста П. Ферма (1601-1665), який у 1629 р. запропонував правила знаходження екстремумів многочленів. Слід підкреслити, що фактично, виводячи ці правила, Ферма активно застосовував граничні переходи, ма­ючи найпростішу диференціальну умову максимуму і мінімуму. Розвитку нового числення сприяли також роботи Р. Декарта (1596-1650), який розробив метод координат і основи аналітичної геометрії.

Систематичне вчення про похідні розвинуто І. Ньютоном (1643-1727) і Г. Лейбніцом (1646-1716), які незалежно один від одного створили тео­рію диференціального числення. Ньютон виходив в основному із задач ме­ханіки (ньютонів аналіз створювався одночасно з ньютоновою класичною механікою), а Лейбніц переважно виходив із геометричних задач. Зокре­ма, до означення похідної Ньютон прийшов, розв'язуючи задачу про мит­тєву швидкість, а Лейбніц — розглядаючи геометричну задачу про прове­дення дотичної до кривої.

У подальшому працями Л. Е й л є р а (1707-1783), О. К о ш і (1789-1857), К. Г а у с с а (1777-1855) та інших математиків диференціальне числення було перетворене в цілісну теорію для дослідження функціональних залеж­ностей.

ІV.  Повідомлення теми і мети уроку.

V.   Актуалізація опорних знань.

  Кожний учень першої групи задає запитання одному з учнів учню з другої групи. Потім кожен учень другої групи задає запитання одному з учнів третьої групи. І кожен учень третьої групи задає запитання одному з учнів першої групи.

           ЗАПИТАННЯ

1. Сформулюйте означення похідної функції в точці.
2. У чому полягає геометричний зміст похідної?
3. Що таке кутовий коефіцієнт прямої? Чому він дорівнює?
4. У чому полягає механічний зміст похідної?
5. Як знайти похідну суми, добутку, частки, складеної функції?
6. Назвіть схему дослідження функції для побудови її графіка.
7. Як знайти найбільше та найменше значення функції на відрізку?
8. В яких точках відрізка неперервна функція може набувати свого найбільшого і найменшого значення?
9. Сформулювати алгоритм дослідження функції на екстремум.
10. Яка точка називається стаціонарною для функції?

   За правильну відповідь учні в своїх картках виставляють собі по 1 балу.

  Кожна група отримує картки з завданням Додаток 1.

  Підбивається підсумок цього етапу уроку.

 VІ Розв'язування вправ

Приклад 1.     Розв'яжіть рівняння 3^х + 3^2-x = 3 • (1 + соs 2πх).            (1)

Коментар

Оскільки у нас немає формул, які б дозволяли перетворювати одночасно і показникові, і тригонометричні вирази, то спробуємо розв'язати задане рівняння, використовуючи властивості відповідних функцій, зокрема, спробуємо оцінити область значень функцій, які стоять у лівій і правій ча­стинах рівняння. Для функції, яка стоїть у правій частині рівняння, це легко зробити і без похідної, а для дослідження функції, що стоїть у лівій частині рівняння, зручно використати похідну.

Розв'язання

ОДЗ заданого рівняння — усі дійсні числа R. Оцінимо ліву і праву час­тини рівняння. Оскільки соs 2πх набуває всіх значень від (-1) до 1, то 1 + соs 2πх набуває всіх значень від 0 до 2. Тоді функція  g (х) = 3∙(1 + соs 2πх) набуває всіх значень від 0 до 6. Отже, 0 < g (х) < 6.

Функцію f(х) = 3^х + 3^2-x дослідимо за допомогою похідної. D(f) = R.

f ' (х) = 3^х ln 3 - 3^{2 – х}ln 3 = 3^{2 – х}ln 3 (3^2x-2 - 1) існує на всій області визна­чення функції f(х).

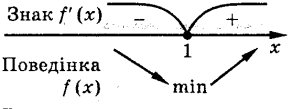f ' (х) = 0, 3^{2 – х}ln 3 (3^2x-2 - 1) = 0. Оскільки 3^{2 – х}ln 3 ≠ 0, то 3^2x-2 - 1=0, 3^2x-2  = 1, 2х - 2 = 0, х =1 — критична точка. Відмічаємо критичну точку на області визначення функції f (х) і знаходимо знаки похідної в кожному з одержа­них проміжків (рис.).

Неперервна функція f (х) має на інтервалі (-∞; +∞) тільки одну кри­тичну точку, і це точка мінімуму (у ній похідна змінює знак з мінуса на плюс). Тоді в цій точці функція набуває свого найменшого значення: f(1) = 6. Отже,  f(x)> 6.

Враховуючи, що g(х) ≤ 6, одержує­мо, що задане рівняння f (х) = g (х) рівносильне системі

Але значення 6 функція f (х) набуває тільки при x = 1, що задовольняє і другому рівнянню системи g (1) = 3 (1 + соs 2πх) = 6). Отже, одержана система (а значить, і задане рівняння) має єдиний розв'я­зок х = 1. Відповідь: 1.

 

Приклад 2.     Розв'яжіть рівняння 2^x+3 +2^2x+1 = 7∙3^x + 3

Коментар

Якщо спробувати застосувати до заданого рівняння схему розв'язуван­ня показникових рівнянь то вдається ре­алізувати тільки перший її пункт — позбутися числових доданків у показ­никах степенів. А от звести всі степені до однієї основи (із зручними показ­никами) чи до двох основ так, щоб одержати однорідне рівняння, чи пере­нести всі члени в один бік і розкласти одержаний вираз на множники — не вдається. Залишається єдина можливість — застосувати властивості відпо­відних функцій. Але і на цьому нам не вдається використати скінченність ОДЗ (вона нескінченна), оцінку лівої і правої частин рівняння (вони обидві в межах від 0 до +∞). Залишається тільки сподіватися на можливість використан­ня монотонності функції. Хоча і тут ми не можемо використати теореми про корені (в обох частинах заданого рівняння стоять зростаючі функції). Тоді спробуємо підібрати корені цього рівняння і довести, що інших коренів воно не має (зручно попередньо звести рівняння до виду f(х) = 0). Послідовно підставляючи х = 0, х = 1, х = 2, х = 3, з'ясовуємо, що f (0) = 0, f (1) = 0, f (3) = 0, тобто рівняння f (х) = 0 має три корені. Щоб довести, що інших коренів немає, достатньо довести, що у функції f (х) не більше трьох проміжків зростання або спадання; а, враховуючи неперервність f (х) на всій числовій прямій, для цього достатньо довести, що у неї не більше двох критичних точок, тобто рівняння f ' (х) = 0 має не більше двох коренів. Роз­глядаючи тепер рівняння f ' (х)= 0, ми після його перетворення можемо провести аналогічні міркування, але вже для двох коренів. Виконуючи перетворення рівняння f ' (х) = 0, врахуємо, що всі його члени мають однаковий степінь - х (тобто воно є однорідним відносно трьох функцій від змінної х, а саме: 2^х, 3^х, 4^х). За до­помогою ділення обох частин рівняння f ' (х) = 0 на степінь з основою 2, 3 або 4 вдається зменшити кількість виразів із змінною на один.

Розв'язання

Задане рівняння рівносильне рівнянню 2^х • 2³ + 2^2х • 2¹ - 7 • 3^х - 3 = 0, тобто

8∙2^x + 2∙4^x -7∙3¹ - 3 = 0.                                      (1)

Позначимо f (х) = 8∙2^x + 2∙4^x -7∙3¹ - 3. Оскільки f (0) = 8 + 2 – 7 - 3 = 0, f (1) =16 + 8 - 21 - 3 = 0,  f (3) = 64 + 128 - 189 - 3 = 0, то рівняння f (х) = 0 має три корені: 0, 1, 3. Доведемо, що інших коренів у рівняння (1) немає. Для цього достатньо довести, що у функції f (х) є не більше трьох проміжків зростання або спадання, а, враховуючи неперервність функції f (х) на всій числовій прямій, достатньо довести, що функція має не більше двох кри­тичних точок.

Область визначення: D (f) = R.

Похідна f ' (х) = 8 • 2^х ln 2 + 2 • 4^х ln 4 - 7 • 3^х ln 3 існує при всіх значеннях х. Отже, критичними точками можуть бути тільки ті значення х, при яких f '(х) = 0. Одержуємо рівняння 8 • 2^x ln 2 + 2 • 4^x ln 4 - 7 • 3^x ln 3 = 0. Оскільки 3^х ≠ 0, то після ділення обох частин останнього рівняння на 3^х одержуємо рівносильне рівняння

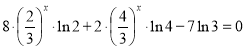                .                             (2)

Щоб довести, що рівняння (2) має не більше двох коренів, достатньо довести, що функція φ(х) = 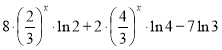, яка стоїть у лівій частині рівняння, має не більше двох проміжків зростання чи спадання, а враховуючи неперервність цієї функції на всій числовій прямій, до­статньо довести, що вона має тільки одну критичну точку. Дійсно,

φ ' (х) = 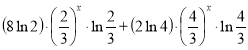 існує при всіх значеннях х. Отже, критичними точками можуть бути тільки ті значення х, при яких φ ' (х) = 0. Одержуємо однорідне рівняння

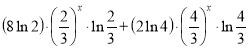      = 0

Оскільки , то після ділення обох частин рівняння на цей вираз   одержуємо   рівносильне   рівняння   .    Звідси

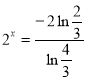 . Враховуючи, що , а , одержуємо, що .

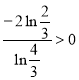Отже, останнє рівняння має єдиний корінь. Тоді функція φ (х) має єдину критичну точку і тому рівняння (2) має не більше двох коренів. Це означає, що функція f (х) має не більше двох критичних точок. Тоді рівняння (1) (а значить, і задане рівняння) має не більше трьох коренів. Але три корені заданого рівняння ми вже знаємо: 0, 1, 3. Отже, інших коренів задане

рівняння не має.

Відповідь: 0, 1, 3.

Приклад 3.     Розв'яжіть нерівність х¹¹ - х⁶ - 2х < -4.

Коментар

Задану нерівність не вдається розв'язати за допомогою рівносиль­них перетворень, тому використає­мо метод інтервалів. Для цього нерівність потрібно привести до виду f (х) 0, де      f (х) — неперервна в кожній точці своєї області визна­чення функція (f (х) — неперервна функція, оскільки це многочлен).

Нагадаємо схему розв'язування нерівності методом інтервалів.

1.  Знайти ОДЗ нерівності.

2.  Знайти нулі функції: f (х) = 0.

3.  Позначити нулі на ОДЗ і знайти знак функції f (х) у кожному з проміжків, на які розбивається ОДЗ.

4.  Записати відповідь, враховуючи знак заданої нерівності.

Для знаходженні нулів функції потрібно розв'язати рівняння f (х)  = 0, яке не вдається розв'язати за допомогою рівносильних перетво­рень, тому для його розв'язування доцільно використати властивості функції f (х), зокрема, її монотон­ність, яку можна обґрунтувати за допомогою похідної.

Розв'язання

Задана нерівність рівносильна нерівності х¹¹ – х⁶ + 2х + 4 < 0. Функція f (х) = х¹¹ – х⁶ + 2х + 4 не­перервна в кожній точці своєї об­ласті визначення, тому для розв'язу­вання нерівності можна використа­ти метод інтервалів.

1.  ОДЗ: х ϵ R.

2.  Нулі функції: f (х) = 0. Знайдемо похідну функції f (х):

f ' (х)= 11 х¹⁰- 6х⁵ + 2. Якщо по­значити х⁵ = t, то f ' (х) = 11t² – 6t + 2. Але квадратний тричлен 11t² – 6t + 2 має від'ємний дискримінант, тоді для всіх t 11t² – 6t + 2  > 0. Отже, для всіх х значення f ' (х) > 0. Тоді функція f  (х)зрос­тає на всій числовій прямій і рів­няння f  (х)= 0 може мати тільки один корінь. Оскільки f (-1) = 0, то х = -1 — єдиний нуль функції f  (х).

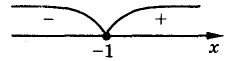3.  Відмічаємо нулі на ОДЗ і знахо­димо знак у кожному з про­міжків, на які розбивається ОДЗ (рис.).

Відповідь: (-∞; -1).

 

Учитель кожній групі роздає картки з завданнями.

 Підведення підсумків даного етапу уроку

 І тепер поняття похідної широко застосовується в різних галузях науки і техніки. Кожному капітану команди було поставлено завдання знайти і розв'язати задачу прикладного змісту яка розв'язується за допомогою похідної.

 І КОМАНДА

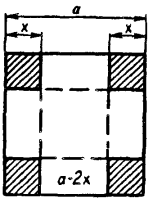
Задача 1. Нехай маємо квадратний лист заліза із стороною а. Треба в кожному куті його відрізати такі квадрати, щоб після згинання країв отримати ящик най­більшої місткості.

 

Розв'язання. Позначимо через х довжину сторони того квадрата, який слід відрізати (мал. 3), а V — об'єм ящика. Тоді V є функцією від х, яка виражається формулою V (х) = (а — 2х)²х,   причому  х  змінюється   на   відрізку

. Оскільки V (х) є неперервною функцією на відрізку то вона набуває на ньому найбільшого значення.

На кінцях відрізка V (х) не може набувати найбільшого значення, бо в цих точках V = 0. Отже, шукана точка міститься всередині відрізка. Знайдемо її. Для цього об­числимо спочатку похідну

V' (х) = — 4 (а — 2х) х + (а — 2х)² = (а — 2х) (а — 6х) і розв'яжемо рівняння (а — 2х) (а — 6х) = 0.

Звідси дістанемо корені х₁ =   і х₂ = . Точка х₁ не є стаціонарною, бо це кінець відрізка, на якому розгля­дається функція V = V (х). Точка х₂ міститься   всередині даного відрізка. Отже, точка х₂ =   є   стаціонарною   і точкою максимуму. У ній функція V = V (х) набуває найбільшого значення, яке дорівнює V= а³

 

 ІІ КОМАНДА

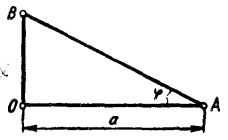Задача 4. Нехай електрична лампочка переміщується (наприк­лад, на блоці) уздовж вертикаль­ної прямої ОВ (мал. 4). На якій відстані від горизонтальної площини слід її розмістити, щоб в точці А цієї площини освітленість була найбільшою (ОА = а)?

 

Розв'язання. З курсу фізики відомо, що освітле­ність прямо пропорційна sin φ і обернено   пропорційна

квадрату відстані АВ = r, тобто Е = k , де k — кое­фіцієнт пропорційності, який залежить від сили світла лампочки.

За незалежну змінну візьмемо висоту х =OB. Тоді

sin φ = , r = ,     0 < x < + оо.

Отже, E = k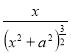  

Знайдемо похідну від E (x):

                                               E'(x)=k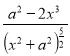

і розв'яжемо  рівняння   k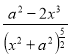= 0

Звідси знаходимо стаціонарну точку х =  .

Оскільки функція Е (х) має тільки одну стаціонарну точку, а в умові задачі сказано, що існує положення лам­почки, при якому освітлення в точці А найбільше, то х є шуканою точкою.

 

 ІІІ КОМАНДА

Задача 5. Визначити розміри такого відкритого ба­сейну з квадратним дном і об'ємом V = 32 м², щоб на об­лицьовування його стін і дна було витрачено найменшу кількість матеріалу.

 

Розв'язання. Позначимо довжину сторони осно­ви через х, а висоту — через у. Тоді V (х, у) = х²у = 32.

Площа бічної поверхні басейну разом із площею дна дорівнює S = х² + 4ху. Знайшовши з попередньої рівності у і підставивши в останню рівність його значення, дістане­мо таку функцію від х:

                   S(x)=x² +

Знайдемо похідну цієї функції: S' (x) = 2x - .

Розв'язуючи рівняння 2х - = 0, зна­ходимо стаціонарну точ­ку х = 4.

Оскільки існує тіль­ки одна стаціонарна точ­ка, то вона і буде точкою мінімуму. Отже, наймен­ші розміри басейну зада­ного об'єму V = 32 м³ такі: х = 4 м; у = 2 м.

 

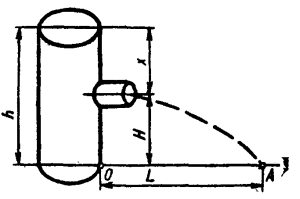Задача 6. Посудина з вертикальною стінкою і ви­сотою Н стоїть на горизонтальній площині (мал. 5). На якій глибині слід розмістити отвір, щоб дальність вильоту води з отвору була найбільшою (швидкість рідини, що ви­тікає за законом Торрічеллі, дорівнює , де х —гли­бина розміщення отвору, g — прискорення вільного па­діння)?

 

Розв'язання. Позначимо через Н відстань отвору в посудині від горизонтальної площини, а через L — від­стань точки А від стінки посудини. Тоді L = Vt, де t — час вильоту води з отвору на площину (у точку А).

З курсу фізики відомо, що t = , або t = .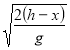

Тоді              L(x) = 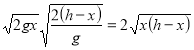0 < x < h.

 Знайдемо похідну L' (x) = ,

Розв'язуючи рівняння        = 0,

знаходимо стаціонарну точку х = .

Оскільки це єдина стаціонарна точка, то вона і буде шуканою.

 

VІІ  Підсумок уроку

 Учитель на дошці  вивішує плакат із словом "ПОХІДНА"  а учні на маленьких папірцях записують слова, пов'язані з цим словом і приклеюють їх навколо плакату ( функція дотична рівняння нерівність, точка, застосування, екстремум, графік, кутовий коефіцієнт, дослідження, задача фізики, електрика, геометрія, механіка…)

 Робота учнів на уроці оцінюється за картками самоконтролю.

 VІІІ Домашнє завдання. Повторити теоретичний матеріал, підготуватися до контрольної роботи. Завдання для самоперевірки №№ 1-18 с. 150-152.

 

 

 

 

 

 

 

ДОДАТОК 1