Тестові завдання з алгебри для учнів 7 класу.

Тестова робота № 1 Лінійне рівняння з однією змінною

І Варіант

1.               Який із записів є рівнянням:

а) 5х + 1 = 20;

б) 2 ∙ 10 - 3;

в) 2х + 3 ≤ 0;

г) 3(18 + 3) = 36?

2. Чи є число 20 коренем рівняння:

а) у – 16 = 82;

б) 5х – 13 = 92;

в) у : 2 +3 = 20;

г) 15 - х = -5?

3. Чи є коренем рівняння х² = 2х +  80 число: х

             а) 0;                   б) 2;                                          

в) 10;                г) -1?

4. Яке з рівнянь є рівносильним даному   4х + 8 = 56:

    а) 4х : 8 =  20;        б) 4х + 8 = 56;           

в) 4( х + 2 ) = 56; г) 4х ∙ 8 = 20?

5. Яке з рівнянь є лінійним:

    а) х² – 2х = 10; б) 2х = 18; в) х²  = 10х; г) х³ – 27 = 0?

6. Яке з рівнянь є зведеним до лінійного рівняння:

а) 6х – 4 = 13 + 2х; б) 3х + 9 = 12;   

в) -5х = -; г) 6х + (13х – 6) = 9?

ІІ Варіант

1. Який із записів є рівнянням:

    а) 55 х  – 35= 7;      б) 17х 34;   

в) 36 : (52 – 16) = 6;  г) 15х = 14 - 25?

2. Чи є число 12 коренем рівняння:

    а) 4х – 8 = 40;    б) у – 3 = 3у;       

в) (х – 5) ∙ 10 = 130; г)  3 + у = 45?

3. Чи є коренем рівняння х + 6 = х² число:

                     а) -3;              б) 0;            

в) 3;              г) 6?

4. Яке з рівнянь є рівносильним даному   15х + 3 = 63:

а) 5х : 5 = 100;            б) 2х ∙ 5 = 45;

в) 5х – 5 = 45;         г) 3(5х + 1) = 63?

5. Яке з рівнянь є лінійним:  

а)1 - х⁴  = 1;                б) х² + 22х = 0;

в) 5х + 18 = 24;             г) х²  = 16?

6. Яке з рівнянь є зведеним до лінійного рівняння:

 а) 12х – 5 = 14х;  б) 23х – 13 = 3 - 4х;

в) (12х – 7) + 2х = 0; г) -2х = 2?

Тестова робота № 2.   Тотожні перетворення виразів.

І Варіант

1. Який з виразів є числовим:

        а) 22 - ав;               б) (13 - х) : 5;

в) + 1;                г) 5 + 5 : 1?

2. Який вираз є виразом зі змінною:

   а) (59 - 7) : 3;              б) 10 : 2 +455;

в) 72 ∙ (6 + 3);           г) (а +1 2) : 25?

3. Який з виразів є цілим:    

          а) ;             б) 6х +1;            

в) ;               г) 126 - 1?

4. Який з виразів є дробовим: 

               а) с - ;          б) ;         

в) ;                  г) с - ?

5. Який з наведених числових виразів не має смислу?

         а) 25 : 5 -3;        б) (123 - 24) : 3;

в) 45 : (-8 + 8);      г) (108 – 15 ∙ 2) : 7.

6. Значення виразу 102х – 108, якщо х = 4 дорівнює:

              а) 300;                            б)400;

         в) - 300;                  г) - 400.

ІІ Варіант

1. Який з виразів є числовим:

             а) 12а + в;            б) 92 - ху;

в) 23 +456 - ;             г) (2 + а) : 4 ?

2. Який вираз є виразом зі змінною:

           а) 52 ∙ 23 - 13;          б) х – 512;      

в) 90 : 3 ∙10;                 г) 0 ∙ 13 + 9?

3. Який з виразів є цілим:    

           а) + 61;            б) ;         

в) х² + 5х; г) - 1?

4. Який з виразів є дробовим:

         а) ;                б) 12х + 1;          

в) ; г) a - ?

5. Який з наведених числових виразів не має смислу?

            а) ;         б) 6 – 2(9 +5);

в) (9 + 11) : 5;              г) .

6. Значення виразу -3х + 12, якщо х = 5 дорівнює:

                         а) 3;                    б) - 3;       

в) -2;                         г) - 5.

Тестова  робота № 3. Степінь з натуральним показником

І Варіант

1.         Записати добуток у вигляді степеня: :

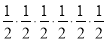                 а) ;             б) ;     

в) ; г) .

2. Записати степінь у вигляді добутку  .

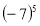 а) -7 ∙ 5; 

б) -7 ∙ (-7) ∙ (-7) ;         

в) -7 ∙ (-7) ∙ (-7) ∙ (-7);    

г) (-7) ∙ (-7) ∙ (-7) ∙ (-7) ∙ (-7).

3.         Обчислити .  

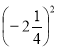           а) -5,5;             б) 5;        

в) - 2;         г) 5.

4.         Розкласти на прості множники 60:

         а) 4 ∙ 3 ∙ 5;         б) 2 ∙ 2 ∙ 3 ∙ 5;    

в) 40 ∙ 2; г) 3 ∙ 2 ∙ 3∙ 2 ∙5.

5.         Обчислити значення  0,2 ∙ 20² .

         а) 80;                    б) 8000;           

в) 800;               г) 8.

ІІ Варіант

1.   Записати добуток у вигляді степеня  3 ∙ 3 ∙ 3 ∙ 3 ∙3 ∙ 3 ∙ 3 ∙ 3 ∙ 3:

          а)3⁶;                    б)3⁹;

        в) 3ⁿ;                     г)3¹⁰.

2.   Записати степінь у вигляді добутку  .

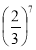а) ∙ 7;

 б) ∙ ∙ ∙ ∙ ;

в) ;

 г) ∙ ∙ ∙ ∙ ∙  ∙ .

3.Обчислити .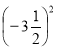

             а) - 14;           б) - 12;

       в) 12;              г) 11.

3. Розкласти на прості множники число 66:

                    а) 33∙ 2;          б) 3 ∙ 2 ∙ 6;        

        в) 2 ∙ 3 ∙ 11;           г) 1 ∙ 66.

4.   Обчислити значення .

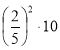                    а) 8;                 б) 44;

               в) 4;                      г) 0,4

5.   Знайти значення виразу   3³ ∙ 2  + 6² .

                      а) 49;              б) 96;

        в) 90;                         г) 93.

Тестова робота № 4. Властивості степеня з натуральним показником

І Варіант

1. Яка з рівностей правильна:

      а) х¹⁸  - х⁶ = х¹⁴;    б) х⁸⁰ : х²²  = х⁵⁸;

в) (х²)⁵  = х¹⁵;             г) х¹⁰  : х⁶ = х².

2. Знайти значення виразу:  ( -4)²  + 4⁰  - 3.

             а) -7;                  б) 10;          

    в) -18;                     г) 14.

3. Виконати піднесення до степеня:   ( - 0,1авс )³.

           а) -0,3а³в³с³;         б) 0,003авс³;

в) -0,001а³в³с³;           г) 0,001 а³в³с³

4. Подати вираз у вигляді степеня:  х¹⁸ ∙ х⁸ : х⁵.

            а) х⁰;                       б) х⁵;                

    в) х³¹;                          г) х¹.

5. Записати вираз у вигляді степеня:  ((х⁸)²)³.

            а) х⁹⁶;                      б) х²⁸;         

      в) х⁴;                       г) х⁴⁸.

6. Замінити зірочку степенем з основою х так, щоб утворилася правильна рівність:     * : х¹⁰ ∙ х⁵  = х¹⁸ .

              а) х³;                     б) х²¹;          

        в) х¹³;                   г) х²³.

ІІ Варіант

1. Яка з рівностей правильна:

     а) а⁵¹  ∙ а⁷¹ = а¹²²;   б) х¹⁰ : х¹⁰  = х²;

в) (а⁶)³  = а¹¹; г) х⁹  ∙ х¹¹ = х¹⁸.

2. Знайти значення виразу:  6¹  + 9 + (-2)⁰.

             а) 15;                   б) 16;           

    в) 0;                      г) 1.

3. Виконати піднесення до степеня:   ( - 0,2хуz )².   

          а) -0,4xyz ²;        б) 0,04x ² y ² z²;

в) -0,4xyz;          г) -0,04x ² y ² z².

4. Подати вираз у вигляді степеня:  х³² : х²² ∙ х¹².

         а) х²²;                    б) х¹⁹;           

в) х²⁴;                   г) х¹⁰.

5. Записати вираз у вигляді степеня:  ((а⁶)²)⁵.

           а) а¹³;                      б) а²⁵;        

в) а⁶⁰;                    г) а¹²⁶.

6. Замінити зірочку степенем з основою х так, щоб утворилася правильна рівність:  х¹²  ∙ * : х¹¹  = х⁵

а) х²²;                       б) х⁰;         

в) х¹¹;                     г) х⁴

.

Тестова робота робота № 5. Одночлен. Дії з одночленами

І варіант

1.   Який вираз є одночленом:    

        а) 16х²  - 25;            б) 2х – 7у;         

в) 5,5ху;                г) 61х – 25х² ?

2.   Назвіть одночлен стандартного вигляду

      а) 18хх² ;         б) р ∙ 7у²;

     в) -15х ∙ 9;             г) 5х⁸ у⁶ .

3.   Знайти значення одночлена 2х² , якщо х = 0,4.

      а) 0,32;              б) 0,2;

      в) 1;                       г)0,5.

4.   Звести одночлен до стандартного вигляду:  - 5а²в ∙ 0,2в³ .

     а) - а²в⁴;             б) - 10авв³;

       в) 0,1авв³;           г) – 0,1а²в⁴ .

5.   Піднести до степеня одночлен  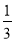( - х²у⁵ )³ .

        а) - х³ у⁵;             б) - х⁶ у¹⁵;

       в) х⁴ у⁵;           г)  х³ у⁶.

6.Який одночлен стандартного вигляду потрібно записати замість * , щоб дістати правильну рівність:     * ∙ 9 х³ у = 36 х⁸ у³ .

   а) 3х³ у²;               б) 2 ∙ 2  ∙ х ∙ х⁴ ∙ у²;

       в) 4 х⁵ у² ;             г) 6х² х³ у².

IІ варіант

1.   Який вираз є одночленом:    

а)1 + 0,9х;                       б) - 62х⁶;

в) 2х² + 1;                г) х + у .

2.   Назвіть одночлен стандартного вигляду:

      а) – 12ху⁵ ;                    б) -х ∙ 2у;

в) 6( - n)m² ;                     г) 15у⁵у² .

3.   Знайти значення одночлена 4х³ , якщо х = 0,1.    

       а) 0,4;                               б) 0,04;

в) 4,1;                            г) 0,004.

4.   Звести одночлен до стандартного вигляду:  0,5ху ∙ ( -2у⁵ ).   

       а) хуу²;                        б) – 2хуу²;

  в) 0,1ху³;                     г) – ху⁶ .

5.   Піднести до степеня одночлен:  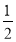( - х³ у⁵ )⁴ .

       а) - х⁶ у⁷;                б)  х¹² у²⁰; 

    в) - х⁷ у⁹;                г) -2х⁸ у¹².

6.   Який одночлен стандартного вигляду потрібно записати замість * , щоб дістати правильну рівність:     2а в⁴ ∙ * = 22а⁷ в⁷.

      а) 2а⁶ в³;                       б) 20а⁵ в³;

в) 11а²а³в³ ;                     г) 11а² а³ вв².

Тестова робота № 6. Многочлен. Додавання та віднімання многочленів

І варіант

1.   Який з виразів є многочленом:

а) (а – 3)(а – 9);     б) 25,2;          

в) х² – х + 15; г) ?

2.   Звести до стандартного вигляду многочлен:    2х  ∙ 5ху²  - 5х² у ∙ у.

  а) 10ху² – 5х² у² ;     б) 10х² у²  - 5х² у;

      в) 5х² у²;       г) 0 .

3.   Обчислити значення многочлена 10х² – х , якщо х = .

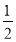      а) 1;                б) 2;                        

    в) 0,4;          г) -0,2.

4.   Знайти суму многочленів:  3х³ -8х + 9 і 3х³ – 7.

     а) 9х⁶ – 2х - 2;            б) х⁵;                

   в) 6х³ – 8х + 2;          г) 6х⁶  - 2.

5.   Знайти різницю многочленів:     4х³  - 2х² + 18  і 3х³ + 2х² – 8.

      а) –х²  + 2х³ - 16;   б) 2х³ - 3х²  - 16;

в) х³ - 2х⁴  + 24;      г) 2х³ - 3х^{2  +} 16 .

6.   Розв’язати рівняння:     13х² – 5х – (13х² – 10х +5) = 0 .

а) коренів немає;            б) х = 1;

в) х = - 1 ;         г) безліч коренів.

ІІ варіант

1.  Який з виразів є многочленом:  

     а) ;                  б) (х -4)(х + 9);

 в) -10,2;                 г) 2у² + 17у - 3 ?

2. Звести до стандартного вигляду многочлен: 2х²у ∙ 3х²у³  - 3х⁴ у² ∙ 2у². 

       а) 6х³у⁴;        б) 6хух² у³ – 6х³у⁴

в) 0;              г) 6х³у⁴  - 6х³у⁴ .

3. Обчислити значення многочлена х³ + 16х² , якщо х = .

         а) 2;                           б) ;

   в) 1;                 г) 1.

4.   Знайти суму многочленів:  5х⁴ +3х³ - 3 і 5х⁴ – 4х³ + 5.

      а) 10х⁸ – х² + 2; б) 10х⁴ – х³  + 2;

в) 10х⁴  + 3х³ – 4х + 2;    г) 6х¹⁰  + 2.

5.   Знайти різницю многочленів:     19х²  + 14х  - 17  і 5х² - 2х  + 9.

а) 4х⁰ + 2х² - 16;       б) 4х⁴ + 2х⁰  - 16;

в) 14х² + 16х  - 26;      г) 4х²  + 6х  - 16

6.   Розв’язати рівняння:     22 - 3х³ – ( - 41 – 3х – 3х³) = 0 .

       а) х = 11;                б) х = - 21;

в) коренів немає ; г) безліч коренів.

Тестова робота № 7. Множення одночлена на многочлен.

І варіант

1. Виконати множення:     4х² (3 + х).  

 а) 12х²  + 5х²;      б) 12х²  + х²; 

в) 12х²  + 4х³;            г) х²  + 12х³.

2. Перетворити добуток у многочлен:    5х (х – 3ху + у²).

а) 3х²  – 6х² у + 3ху² ;б)4х – 5ху+3ху²;

в) 5х²  - 15х²у + 5ху²; г)3х² -х- у+3ху².

3. Записати замість * такий одночлен, щоб виконувалася рівність:

       (ах + в) ∙ * = 4арx +4вр.       

       а) 2в;                    б) р;           

    в) 2р;                        г) 4р.

4. Виконати множення: 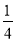  х²у² (1,6х² – 12у³).

а) 0,4х⁴у² – 3х²у⁵;    б) 4х⁴у² – 3х²у⁶;

в)1,85х⁴у² –11,75х²у⁵; г)0,4х⁴у²-3х²у⁶.

5. Перетворити у многочлен:   7а (а – 4в) + 2в (2в – 3а).

      а) 28а²  + в²; б) 7а – 14ав + в²;

в) 7а² – 34ав+ 4в²; г) а² – 28ав + в².

6. Розв’язати рівняння:     6а + 3(5 – 2а) = 0 .

а) безліч коренів;       б) а = 6;

в) а = - 6 ;          г) коренів немає.

ІІ варіант

1. Виконати множення:     - 9х⁵ (х + 1).  

       а) - 9х⁴  - х³;         б) - 9х⁶  - 9х⁵;

в) - 9х⁴  - 18х³;         г) - 9х⁶  + 9х⁵.

2. Перетворити добуток у многочлен:    2х (3х – х² - 5у).

а)6х²  – 2х³  - 10ху ; б)8х² – 4х³ – 8ху;

в) 4х  - 3х² - 8ху; г) 6х²  – 4х³ – 8ху.

3. Записати замість * такий одночлен, щоб виконувалася рівність:

     *  ∙  (ху - в) = 13аху - 13ав.      

          а) 13;                      б) а;

в) 3а;                            г) 13а.

4. Виконати множення:   ху⁵ (1,4у²  – 4х³).

а) 0,7ху⁷ – 2х⁴у⁵;        б) 7ху⁴ – х⁴у³;

в) 0,7ху⁵  – 7х⁴у³; г) 1,4ху⁵ – 3,5х⁴у³.

5. Перетворити у многочлен:   5х (х – 5у) + 5у (у – х).

а) 3х -7ху + 4у; б) 2х² – 7ху + 3у²;

в) (2х + 3у)(-у); г) 5х²  - 30ху + 5у².

6. Розв’язати рівняння:     2(3 + 3х) – 6х = 0 .

    а) коренів немає; б) х = – 0,6;

в) х = 0,6 ; г) безліч коренів.

Тестова робота № 8. Розкладання многочленів на множники  способом  винесення множника за дужки

І варіант

1. Винести за дужки спільний множник:     2а - 18а.

а) 3(3а - 6а);          б) 2(а - 9а);

в) а(9а – 18);                г) 9а(а – 2).

2. Подайте у вигляді добутку: 10х - 6х + 2х.

а) 2(5х - 3х+ х);       б) 2х(4х- 2х);

в) 2х(4х- 2х + 1);   г) х( 8х- 4х + 2).

3. Розв’язати рівняння: а- 10а = 0.

              а) 0;                    б) 0; -10;

    в) – 5; г)                   г) 10; 0.

4. Розкласти на множники вираз:   9(х – у) + 5рх – 5ру.

    а) 2р(х – у);       б) (9 – 5р)(х – у);

в) (х – у)(2р + а);           г) 2рху.

5. Подати у вигляді добутку:  - 25х⁶ - 50х.

а) – 25(х- 5х);      б) – 5х(х- 4х);

в) – 25х(х⁴+ 2); г) - х(15х + 20).

6. Розкласти на множники вираз:   рв + рс + 14в + 14с. 

а) а(в + с) + 4(в + с);

б) в(а + 4) + с(а + 4);

в) (ав + 4с)(ас + 4с);

г) (в + с)(р +14).

ІІ варіант

1. Винести за дужки спільний множник:     8ху + 12х.

    а) 4(2ху + 3х);     б) 6(2ху + 2х);

в) х(8у + 12х);         г) 6х(3у + 2х).

2. Подайте у вигляді добутку:  25у + 15у - 5у.

а) у(у + 2у - 1);    б) 5у(5у+ 3у - 1);

в) 5у(3у+ у);        г) 5(3у + 2у- у).

3. Розв’язати рівняння:   29в - в = 0.

           а) – 29; 0;                      б) 29;

 в) 7;                        г) 0; 29.

4. Розкласти на множники вираз:   рх + ру - 12(х + у).

    а) 3р(х + у);        б) (х - у)(р + 3);

в) (х + у)(р - 12); г) (х + у)(3 – р).

5. Подати у вигляді добутку:  - 64у+ 16у.

а) – 64у(4у- 1);       б) – 16у(4у- 1);

в) – 4у(4у + 16);         г) 4(у – 16у).

6. Розкласти на множники вираз:   ру + ра + 26у + 26а.

а) х(у + а) + 6(у + а);

б) у(х + 6) + а(х + 6);

в) (а + у)(р + 26);

г) (ху + 6а)(ха + 6у).

Тестова робота № 9. Множення многочлена на многочлен

І варіант

1. Спростити вираз:     (х + 5)(х - 2).

    а) 2х - 12;             б) х +3х - 10;

в) х – 3х  +  12;            г) х + х - 12.

2. Подайте у вигляді многочлена вираз:  (х + у)(с – р ).

а) хс – хр + су - ру;

б) хс + хр – су + ру;

в)  сх – хр – ус - ру;

г) сх – рх – су + ру.

3. Спростити вираз:   (х – 5)(2х + 5) + 20.

    а) 4х – 12х;             б) 2х³ – 5х - 2;

в) 3х+ х + 5;             г) 2х + х + 45.

4. Виконати множення:   (2а + 7)(в – 3).

    а) ав + 7 - 21;           б) ав - 7;

в)2ав – 6а + 7в - 21; г)ав – а + 7в - 1.

5. Розв’язати рівняння:    (а – 4)(2 + а) - а = 0.

               а) 4;                    б) - 5;

     в) 20;                           г) - 20.

6. Спростити вираз і обчислити його значення  (5х – 2)(2х + 1) – 10х,

    якщо х = - 2.

                  а) 6;                 б) - 4;

          в) 4;                     г) 14.

ІІ варіант

1. Спростити вираз:     (у +2)(у - 3).

  а) 2у - 6;                    б) у - у - 6;

в) у– 6;                  г) у+ у - 6.

2. Подайте у вигляді многочлена вираз:  (с + р)(х - у).

а) сх + су + рх + ру;

б) рх – ру – вх - ву;

в)  сх – су + рх - ру;

г) сх + су – рх + ру.

3. Спростити вираз:   (у - 5)(4у – 2) + 12.

    а) 5у + 12у;             б) 4у + 7у;

в) 4у - 20у + 12;         г) 4у + 10у.

4. Виконати множення:   (х - 5)(у + 4).

      а) ху - 16;             

б) ху + 16;

в)ху – 8у + 2х + 16;

г)ху + 4х – 5у - 20.

5. Розв’язати рівняння:    (х + 12)(5 - х) + х+ 10 = 0.

            а) 4;                          б) - 10;

в) - 1;                          г) 10.

6. Спростити вираз і обчислити його значення  (6 – 2х)(х - 1) + 2х,

    якщо х = 2.

            а) 10;                       б) 16;

   в) - 10;                     г) - 44.

Тестова робота № 10. Розкладання многочленів на множники способом групування

І варіант

1. Розкласти на множники:   рх – ру + 9х – 9у.

а) р(х – у) + 9(х – у);

б) (х – у)(р + 9);

в) х(а + 9) + у(а – 9);

г) х(а + 9) – 7(а + 9).

2. Подати у вигляді добутку многочленів вираз:   18х –18у + 5ах – 5ау.

    а) 18(х – у) + 5а(х – у);

б) 5(2х – 2у + ах – ау);

в) (х -у)(18 + 5а);

г) 5(х + у)(2 + а).

3. Розкласти на множники:     2(х - у) + рх - ру.

а) р(х + у) + 2(х + у);

б) (х + у)(р – 2);

в) (х – у)(х + у);

г) (х - у)(2 + р).

4. Подати у вигляді добутку многочленів:      1 – рх – х + р.

а) (1 + р) – х(р + 1); б) (1 + р)(х – 1);

в) (1 – р)(х + 1);   г) (р + 1)(1 – х).

5. Обчислити значення виразу найзручнішим способом: 

    82 ∙ 15 + 18 ∙15 + 13 ∙ 2 + 17 ∙ 2.

         а) 1030;                б) 1560;         

          в)1600;             г) 4200.

6. Розв’язати рівняння:   2х(х + 1) + 12(х + 1) = 0. 

        а) 0; - 1;                 б) - 1;

        в) – 2; 0;             г) – 6; - 1.

ІІ варіант

1. Розкласти на множники:   9х + 9у – рх - ру.

    а) 10(х + у) - а(х + у);

    б) х(9 - и) + у(9 - р);

в) р(х + у) + р(х - у);

г) (9 - р)(х + у).

2. Подати у вигляді добутку многочленів вираз:   16ах + 16ау + 4х + 4у.

а) 4(х + у)(2а + 1);

б) 16а(х + у) + 4(х + у); 

в) 4(х + у)(4а + 1);

г) 4(2ах + 2ау + 3х + 3у).

3. Розкласти на множники:     7х + 7у + р(х + у).

а) 7(х + у) + в(х + у);

б) (х + у)(7 – р);

в) (х – у)(7 + р);

г) (х + у)(7 + р).

4. Подати у вигляді добутку многочленів:      13 – су – 13у + с.

а)13(1 - у) + с(1 - у);

б) 13(1 - у) - с(у – 1);

в) (1 – у)(13 + с);

г) (13 - с)(у – 1).

5. Обчислити значення виразу найзручнішим способом: 

    7 ∙ 84 + 7 ∙ 16 + 3 ∙ 14 + 3 ∙ 16.

                   а) 740;                      б) 790;

в) 700; г)730

6. Розв’язати рівняння:   6(х - 9) + 2х(х - 9) = 0.    

           а) 0; 9;                        б) – 3;  9;   

в) 0; 3;              г) – 3; - 9.

Тестова робота № 11. Квадрат суми і квадрат різниці

І варіант

1. Який вираз є квадратом суми двох виразів:

    а) 2х + 3у;          б) (3х + 9у);

    в) (х + у);                   г) (х + у)?

2. Подати у вигляді многочлена:   (р + с).

а) р + с;               б) р + рс + с;

в) 2р + 2с; г) р + 2рс + с.

3. Перетворити у многочлен:     (6х - 5у).

а) 18х – 25у;     б) 81х -  36ху + 4у;

в) 36х – 60ху + 25у;г) 36х - 25у.

4. Спростити вираз:      (х – 3) + х(х – 6).

а) 2х + 1;              б) 2х - 4х + 1;

    в) – 4х + 1;              г) 2х - 12х + 9.

5. Спростити вираз:   24х + (-х + 6).

    а) 25 + х + 25х;           б) 36 + х;

      в) 3х + 10;            г) 25 + 5х + х.

6. Розв’язати рівняння:   (х - 4) - х = 40. 

               а) 3;                         б) - 3;

      в) – 2;                      г) – 2; 0.

ІІ варіант

1. Який вираз є квадратом суми двох виразів:

       а) (х + у);             б) х + у;

      в) (х + у);                г) (х + у)?

2. Подати у вигляді многочлена:   (р - в).

    а) р - рв + в; б) р - 2рв + в;

в) р + 2рв - в; г) р - в.

3. Перетворити у многочлен:     (2х + 4у).

а)  4х + 16у; б) 4х + 16ху + 16у;

в) 4х +  12ху + 16у; г) 14х + 9у.

4. Спростити вираз:      (х + 5) - х(х – 10).

    а) 2х + 5х + 4;          б) 20х + 25;

 в) 20х+ 25;          г) 2х + 3х + 4.

5. Спростити вираз:   (2х + у) - 4ху.

а) 2х + 2у – 3ху;       б) 4х + у;

в) х - 2ху + у;       г) х -  ху + у.

6. Розв’язати рівняння:   (5х - 1) - 25х = 11. 

                  а) 3;                     б) – 2;

         в)  2;                    г) – 3.

Самостійна робота № 12. Розкладання многочленів на множники за допомогою формул квадрата суми і квадрата різниці

І варіант

1. Розкласти на множники:      4а - 12а + 9.

          а) а(а – 8) + 16; б) а - 8(а + 2);

в) (а + 4)(а + 4) – 8а; г) (2а - 3).

2. Обчислити значення виразу:   а - 6а + 9, якщо а = 3.

                  а) 0;                        б) 1;

       в) 2;                г) 3.

3. Обчислити зручним способом:     5 + 2 ∙ 5 ∙ 35 + 35.

                  а) 25;                   б) 250;

        в) 400;                           г) 1600.

4. Перетворити тричлен у квадрат двочлена:     9 х - 30ху + 25у.

    а) (9х –25 у);               б) (х + у);

      в) (3х – 5у);              г) (2х – у).

5. Розкласти на множники многочлен:   х + 8ху + 9ху.

    а) (х + 3у);                  б) (х – 3у);

      в) х(х +3 у);             г) х(3х – у).

6. Розв’язати рівняння:   х - 12х + 36 = 0. 

                 а) - 4;                  б) 6;

        в) – 6;                      г) 4.

ІІ варіант

1. Розкласти на множники:      х + 14х + 49.

а) х(х + 7) + 27;

б) (х + 7); 

в) (х + 7)(х + 7) + 10х;

 г) х+7(2х + 5).

2. Обчислити значення виразу:   х - 10х + 25, якщо х = - 5.

                         а) - 3;                 б) - 2;

              в) 0;                    г) 1.

3. Обчислити зручним способом:     9 + 2 ∙ 9 ∙ 21 + 21.

                         а) 9;               б) 90;

        в) 900;              г) 0,9.

4. Перетворити тричлен у квадрат двочлена:     4а + 4ав + в.

          а) (а – в);           б) (а + в);

      в) (2а + в);          г) (а + 2в).

5. Розкласти на множники многочлен:   у + 72ау + 36ау.

             а) у(у + 6а);       б) (у – а)у;

    в) (у + а);              г) (у – а).

6. Розв’язати рівняння:   100х + 60х + 9 = 0. 

              а) – 0,3;                  б) 9;

         в) – 9;                 г)0,3.

Самостійна робота № 13. Множення різниці двох виразів на їх суму

І варіант

1. Виконати множення многочленів:   (3в + с)(3в – с).

    а) 9в + с;           б) 9в - с;      

в) в + 2вс + с;        г) в - 2вс + с.  

2. Подати у вигляді многочлена добуток:   ( 5а – 1)(5а + 1).

а) 4а - 24а + 36;      б) 25а + 1;

  в) 25а + 4а + 1;      г) 25а - 1.

3. Спростити вираз:     (2х – 3)(2х + 3) + 9.   

         а) 4х + 18;       б) 4х - 18; 

в) 4х;                      г) 4х - 12х.

4. Значення виразу:     (10 + 1)(10 – 1).

            а) 39;                      б) -99;

 в) 99;                          г) 90.

5. Спростити вираз:  49х²  + (9 – 7х)(7х + 9) - 10.

    а) – 49х + 14;      б) – 49х - 6;

       в) 71;                      г) – 71.

6. Знайти корені рівняння:   (5х – 2)(5х + 2) – 2х = 25х. 

    а) 0,5;                      б) ;

         в) – 2;                г) 2.

ІІ варіант

1. Виконати множення многочленів:     (3х - а)(3х + а).

     а) х - 2ах + а; б)9х + 2ах + а;

в) 9 х- а;          г) х - а.

2. Подати у вигляді многочлена добуток:   (5а - 1)(5а + 1).

    а) 9а + 24а + 16; б) 25а - 1;

в) 5а - 2а + 16;         г) 25а + 1.

3. Спростити вираз:     (х + 7)(х - 7) - х.

       а) 2х - 4;        б) - 49;

в) х - 4х - 49;          г) 2х + 4х - 49.

4. Значення виразу:     (50 + 1)(50 – 1).

        а) 61;                 б) 200;

  в) 249;                    г) 49.

5. Спростити вираз:   81а - (9а – 1)(1 + 9а) + 13.

      а) 12а + 14;           б) 14;

   в) 12а;                 г) 12а - 14.

6. Знайти корені рівняння:   (х - 2)( х + 2) – 4х = х. 

                    а) - 1;            б) ;

  в) 1;                  г) - .

Тестова  робота № 14. Розкладання на множники різниці квадратів двох виразів

І варіант

1. Подати многочлен у вигляді добутку різниці і суми:   0,09 - х.

а) (0,03 – х)(0,03 + х);

б) (0,3– х)(0,3 + х);

в) (0,3 + х)(х - 0,3);

г) (0,03 + х)(х - 0,03).  

2. Розкласти на множники:   25а - 9в.

а) (5а – 9в)(5а + 9в);

б) (5а + 9в)(5а + 9в);

в) (5а – 3в)(5а + 3в);

г) (2а + 3в)(3в - 2а).

3. Розв’язати рівняння:     х - = 0.

               а);               б) ; 

    в) - ;                         г) - і .

4. Обчислити:     27 - 17.

       а) 440;                  б) 140;

     в) 44;                        г) 40.

5. Подати  у вигляді добутку:   ху - 25.

 а) (х –5)у;        б) х(у – 5);

в) (ху – 5)(ху + 5);  г) (ху + 2)(ху – 2).

6. Добрати замість  ∙ ∙ ∙  множник так, щоб рівність перетворилася на

    тотожність:     а - 16 = (а + 4)( ∙ ∙ ∙  ). 

         а) а + 4;                  б) а – 4;

      в) а;                   г) - 4.

ІІ варіант

1. Подати многочлен у вигляді добутку різниці і суми:    х - 0,49.

    а) (х – 0,7)(х + 0,7);

б) (х – 0,07)(х + 0,07);

в) (х + 0,7)(0,7 - х);

г) (х + 0,07)(0,07 - х).  

2. Розкласти на множники:   49а - 64в.

    а) (7а – 4в)(7а + 4в);

    б) (7а + 8в)(7а + 8в);

в) (7а + 8в)(7в – 8а);

г) (3а + 2в)(3а – 2в).

3. Розв’язати рівняння:     х -  0,81 = 0.

        а) 0,9;                  б) – 0,9; 

 в) 0,81;          г) – 0,9; 0,9.

4. Обчислити:     52 - 42.

           а) 10;               б) 940;     

        в) 94;                  г) 900.

5. Подати  у вигляді добутку:   9 - ав.

 а) (3 - а)в;  б) (9 - ав)(9 + ав)

в) (3 -  ав)(3 + ав); г) а(3 – в).

6. Добрати замість  ∙ ∙ ∙  множник так, щоб рівність перетворилася на

    тотожність:   25 - а = (5 - а)( ∙ ∙ ∙  ). 

                  а) 5 - а;            б) 5 + а;

в) 25 + а;                 г) 5.

Тестова робота № 15. Сума і різниця кубів

І варіант

1. Розкласти на множники:   х - 8.

 а) (х– 4)(х –2); б)(х - 2)(х- 2х + 4);

в) (х - 2)(х + 4х + 4); г)(х - 2)(х+2).  

2. Подати у вигляді многочлена:   (х + у)(х - ху + у). 

       а) х + у;         б) х + у;