Тестові завдання з алгебри для учнів 7 класу (ІІ семестр).
Тестова робота № 17. Функція. Способи завдання функції. Графік функції
І варіант
1. Яка із залежностей є функцією?
а) х = 2у - ![]() ; б) х
; б) х![]() = у + у
= у + у![]() ;
;
в) хук = 5; г) х![]() + ху + а
+ ху + а![]() = у
= у![]() .
.
2. Функцію задано формулою у = 2х – 1. Знайти значення функції, що відповідає значенню аргументу - 5:
а) 11; б) - 11;
в) - 7; г) 5.
3. Знайти значення аргументу, при якому функція у = 7х + 1 набуває значення 50.
а) 7; б) 14;
в) - 14; г) - 7.
4. Знайти область визначення функції: у = 3![]() .
.
а) будь-яке число;
б) будь-яке число, крім 3;
в) будь-яке число, крім - 1;
г) будь-яке число, крім 1.
5. Не виконуючи побудови графіка, знайти нулі функції: у = 5х - 15.
а) -5; б) 5;
в) 3; г) – 3.
6. Яка з точок належить графіку функції: у = 5х – 20?
а) (6; 10); б) (-6; - 10);
в) (1; 5); г) (- 8; - 10).
ІІ варіант
1. Яка із залежностей є функцією?
а) а![]() = а +х + в
= а +х + в![]() ; б) авск = 7;
; б) авск = 7;
в) а![]() у + ау
у + ау![]() - у = х; г) а = 0,5 -
- у = х; г) а = 0,5 - ![]() в.
в.
2. Функцію задано формулою у = 10 – 2х. Знайти значення функції, що
відповідає значенню аргументу - 1:
а) 0; б) 12;
в) - 2; г) 12.
3. Знайти значення аргументу, при якому функція у = 4х + 5 набуває значення – 15.
а) - 2; б) – 5;
в) 2; г) 5
4. Знайти область визначення функції: у = 5![]() .
.
а) будь-яке число;
б) будь-яке число, крім 1;
в) будь-яке число, крім 7;
г) будь-яке число, крім - 1.
5. Не виконуючи побудови графіка, знайти нулі функції: у = 8х - 16.
а) - 2; б) 2;
в) 0; г) 0,2.
6. Яка з точок належить графіку функції: у = 5х + 25?
а) (0; 25); б) (-5; - 1);
в) (0; 5); г) (0; - 5).
Тестова робота № 18. Лінійна функція, її графік та властивості
І варіант
1. Яка з функцій є лінійною функцією:
а) у = 2х5 - 5х![]() ; б) у = 2х3 + 7;
; б) у = 2х3 + 7;
в) у = ![]() ; г) у = х – 1?
; г) у = х – 1?
2. Функцію задано формулою у = - 0,25х + 5. Знайти значення функції у, якщо х = 8.
а) - 25; б) 25;
в) - 15; г) 15.
-
Не виконуючи побудови графіка функції у = 1
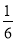 х + 5 з’ясувати, чи проходить
х + 5 з’ясувати, чи проходить
цей графік через точку:
а) (0; - 3); б) (12; 6);
в) (- 6; 12); г) (6; 12).
4. Яка з функцій є прямою пропорційністю:
а) у = 15; б) у = - 222![]() х;
х;
в) у = - ![]() ; г) у = 15х + 4?
; г) у = 15х + 4?
5. Не виконуючи побудови, знайти нулі функції: у = - 3,5х + 1.
а) 0; б) 4;
в) 1 г) – 1.
6. Графік якої функції проходить через точку (0; - 6):
а) у = 5![]() х; б) у = 3х - 6;
х; б) у = 3х - 6;
в) у = - 6х + 6 ; г) у = 2х - 2.
ІІ варіант
1. Яка з функцій є лінійною функцією:
а) у = 2х![]() + 1; б) у =
+ 1; б) у = ![]() + 1;
+ 1;
в) у = ![]() - 5х; г) у = - 12 + 4х?
- 5х; г) у = - 12 + 4х?
2. Функцію задано формулою у = 0,65х + 0,5. Знайти значення функції у, якщо х = 10.
а) - 6; б) 6;
в) 7; г) – 7.
-
Не виконуючи побудови графіка функції у =
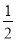 х - 7 з’ясувати, чи проходить цей графік через точку:
х - 7 з’ясувати, чи проходить цей графік через точку:
а) (7; 3); б) (7; 0);
в) (- 7; 7); г) (0; - 7).
4. Яка з функцій є прямою пропорційністю:
а) у = - 5![]() ; б) у = 9;
; б) у = 9;
в) у = ![]() ; г) у = 4х – 2х2?
; г) у = 4х – 2х2?
5. Не виконуючи побудови, знайти нулі функції: у = 0,9х – 5,4.
а) - 8; б) 10;
в) 8; г) 6.
6. Графік якої функції проходить через точку (- 1; - 7):
а) у = ![]() х; б) у = 3х - 4;
х; б) у = 3х - 4;
в) у = - 6,5х; г) у = 12х - 12.
Тестова робота № 19. Рівняння з двома змінними. Лінійне рівняння з двома змінними
І варіант
- Яке з рівнянь є лінійним рівнянням:
а) 2х – 6у =0; б) ![]() =73;
=73;
в) 5х2 – 2х3 = 5; г) 2х2 + 2у2 = 20?
- Яке з рівнянь є рівнянням з двома змінними:
а) х4– 2х + 9 = 0; б) ![]() +
+ ![]() +
+ ![]() = 8;
= 8;
в) 52х + 13у = 5; г) х2 – 9 = 0?
- Яка з пар чисел є розв’язком рівняння: 8х – 5у = 1?
а) (2; 3); б) (-1; 3);
в) (3; 2); г) (0; 4).
- Розв’язком якого з рівнянь є пара чисел (0; -2)?
а) 2х – у = 2; б) 3х2 – у = 5;
в) 4х + 3у = - 7; г) (х – 2)(у – 4) = - 10.
- Виразити з рівняння 3х + 2у = 4 змінну у через х:
а) 2у = 4 – 3х; б) 3х = 4 – 2у;
в) у = 8 – 2х; г) х = 8 - ![]() у .
у .
- Виразити з рівняння 5х – 6у = 10 змінну х через змінну у:
а) 12у = 3х - 5; б) 5х = 3 + 2у;
в) х = 2 + 1,2у ; г) у = 2,5х – 1,5.
ІІ варіант
- Яке з рівнянь є лінійним рівнянням:
а) ![]() = 4; б) – 9х – 2у = 0;
= 4; б) – 9х – 2у = 0;
в) х2 + у2 - z2 = 12; г) 3х2 – у = 3?
- Яке з рівнянь є рівнянням з двома змінними:
а) 2у – 14х = 0; б) 5х2 + х + 7 = 0;
в) х3 + у3 + 5z3 = 4; г) 7х5 – 3у = 8
- Яка з пар чисел є розв’язком рівняння х + 5у = 15?
а) (0; 3); б) (5; 2);
в) (0; - 3); г) (3; - 3).
- Розв’язком якого з рівнянь є пара чисел (2; 1)?
а) (х – 3)(у + 5) = - 8; б) 4х +3у = 14;
в) х2 - 2у = 3; г) 6х – 5у = 7.
- Виразити з рівняння 5х – 2у = 9 змінну у через х:
а) у = 4,5 + 2,5х; б) 5у = 5х - 9;
в) х = ![]() у +
у + ![]() ; г) 4х = 3у + 2.
; г) 4х = 3у + 2.
- Виразити з рівняння 2х + 5у = 14 змінну х через змінну у:
а) 2х = 4 – 3у; б) 5у = 14 – 2х;
в) х = 2 – 1,5у; г) у = 2,8 – 0,4у.
Тестова робота № 20. Графік лінійного рівняння з двома змінними
І варіант
- Яка з даних точок належить графіку рівняння 5х – у = 4:
а) А(1; 1); б) В(6; 1);
в) С(2; 1); г) Р(6; 2)?
- Графік якого рівняння проходить через точку А(3; - 1):
а)4 х - 2у = 2; б) 5х + у = 7;
в) х – 2у = 5; г) 0х + 2у = 4?
- Графік якого рівняння проходить паралельно осі Оу?
а) 12х + у = 6; б) 0х + 4у = 4;
в) 5х + 0у = 20; г) х – 14у = 14.
- Графік якого рівняння проходить паралельно осі Ох?
а) х + 3у = 4; б) 0х – 3у = 3;
в) 3х – у = 0; г) 2х + 0у = 6.
- Графік якого рівняння паралельний графіку рівняння у – 2х = 3:
а) 13х + 5у = 2; б) 2у – 4х = 6;
в) – 2у + х = 5; г) у + 0х = 2?
- При якому значенні а графік рівняння - 2х + 5у = а проходить через точку (1; 1)?
а) 3; б) - 2;
в) - 3; г) - 5.
ІІ варіант
- Яка з даних точок належить графіку рівняння х + 5у = 2:
а) А(2; 3); б) В(2; 1);
в) С(2; 0); г) Р(5; - 1)?
- Графік якого рівняння проходить через точку В(-1; 5):
а) 5х - 2у = 10; б) - х + 2у = 16;
в) - 2х – 2у = 8; г) 0х - 3у = 18?
- Графік якого рівняння проходить паралельно осі Ох?
а) 7х + 14у = 7; б) 0х + 20у = 4;
в) 21х + 0у = - 6; г) 5х – 4у = 12.
- Графік якого рівняння проходить паралельно осі Оу?
а) х + 0у = 4; б) 0х – 5у = 5;
в) 7х – у = 7; г) 2х + 0у = 6.
- Графік якого рівняння паралельний графіку рівняння 2у + х = 4:
а) 0у – 2у = 3; б) 4у + 3х = 12;
в) 2у - х = 8; г) 4у + 2х = 5?
- При якому значенні в графік рівняння 3х + 2у = в проходить через точку (1; 2)?
а) 7; б) 14;
в) - 16; г) - 5.
Тестова робота № 21.Системи лінійних рівнянь з двома змінними. Способи розв’язування розв’язування: графічний та спосіб підстановки
І варіант
- Яка із систем є системою двох лінійних рівнянь з двома змінними:
а) 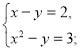 ; б)
; б) 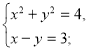 ;
;
в) ![]() ; г)
; г)![]()
-
Яка пара чисел є розв’язком системи:
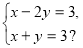
а) (1; 2); б) (0; 2);
в) (2; 3); г) (3; 0).
- Розв’язком якої системи є пара чисел (2; 3):
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]()
-
Скільки розв’язків має система лінійних рівнянь:
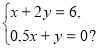
а) 1 розв’язок; б) безліч розв’язків;
в) жодного розв’язку; г) 2 розв’язки.
-
У якій рівності правильно виконано підстановку для розв’язування системи рівнянь
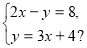
а) 2(3х + 4) – у = 8; б) 2х – (3х – 4) = 8;
в) 2х – (3х + 4) = 8; г) 2х +(3х + 4) = 8.
- Не виконуючи побудов, знайти координати точки перетину графіків рівнянь: 5х + 2у = 7 і х – 2у = - 1.
а) (3; 0); б) (1; - 1);
в) (1; 1); г) (2; 1).
ІІ варіант
- Яка із систем є системою двох лінійних рівнянь з двома змінними:
а) ![]() ; б)
; б) 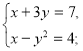 ;
;
в) 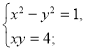 ; г)
; г)![]()
-
Яка пара чисел є розв’язком системи
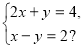
а) (2; 1); б) (4; 0);
в) (2; 0); г) (4; 1).
- Розв’язком якої системи є пара чисел (- 1; 2):
а) ![]() ; б)
; б) ![]() ;
;
в) ![]() ; г)
; г) ![]()
-
Скільки розв’язків має система лінійних рівнянь:
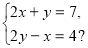
а) 1 розв’язок; б) безліч розв’язків;
в) жодного розв’язку; г) 2 розв’язки.
-
У якій рівності правильно виконано підстановку для розв’язування системи рівнянь
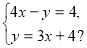
а) 4х + (3х + 4) = 8; б) 4х – (3х – 4) = 4;
в) 4х – (3х + 4) = 4; г) 4(3х + 4) - у = 4.
- Не виконуючи побудов, знайти координати точки перетину графіків рівнянь:
х - 2у = 5 і 3х + 2у = 3.
а) (- 4; 2); б) (4; 3);
в) (4; - 3); г) (2; - 1,5).
Тестова робота № 22. Розв’язування систем лінійних рівнянь способом додавання. Розв’язування задач за допомогою систем лінійних рівнянь
І варіант
-
Яке рівняння можна отримати, якщо почленно додати рівняння системи:
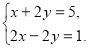
а) 3х + 4у = 6; б) 3х = 6;
в) 3х – 4у = 6; г) 3х – 4у = 4.
-
На яке число треба помножити обидві частини другого рівняння системи, щоб дістати у рівняннях протилежні коефіцієнти при змінній х:
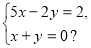
а) 5; б) 2;
в) - 5; г) - 2.
-
На яке число треба помножити обидві частини першого рівняння системи, щоб дістати у рівняннях протилежні коефіцієнти при змінній у:
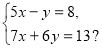
а) 6; б) 7;
в) - 6; г) 5.
-
Знайти розв’язок системи рівнянь способом додавання:
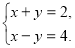
а) (2; 1); б) (3; 1);
в) (2; -1); г) (3; -1).
- У кошику 24 кульки білого та чорного кольорів. Відомо, що білих кульок на 2 більше, ніж чорних. Яка система відповідає умові?
а) ![]() б)
б) ![]()
в) ![]() г)
г) ![]()
- Скласти систему рівнянь, що відповідає умові задачі.
Зошит коштує х грн, а щоденник у грн. Разом вони коштують 3 грн. За два
щоденника заплатили на 3 грн більше ніж, за три зошити. Скільки коштує
один зошит і один щоденник?
а) ![]() б)
б) ![]()
в) ![]() г)
г) ![]()
ІІ варіант
-
Яке рівняння можна отримати, якщо почленно додати рівняння системи:
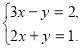
а) 5х + 2у = 3; б) 5х – 2у = 3;
в) 5х = 3; г) 5х + 2у = 1.
-
На яке число треба помножити обидві частини другого рівняння системи, щоб дістати у рівняннях протилежні коефіцієнти при змінній х:
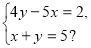
а) 4; б) 5;
в) - 4; г) - 5.
-
На яке число треба помножити обидві частини першого рівняння системи, щоб дістати у рівняннях протилежні коефіцієнти при змінній у:
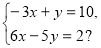
а) - 5; б) 5;
в) 6; г)- 6.
-
Знайти розв’язок системи рівнянь способом додавання:
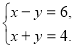
а) (4; 2); б) (2; 4);
в) (5; 1); г) (5; -1).
- У кошику 36 яблук і груш. Яблук на 10 менше, ніж груш. Яка система відповідає умові задачі?
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()
- Скласти систему рівнянь, що відповідає умові задачі.
Ручка коштує х грн., а блокнот у грн.. Разом вони коштують 3 грн. Чотири
ручки і три блокнота заплатили 10 грн. Скільки коштує одна ручка і скільки
коштує один блокнот?
а) ![]() б)
б) ![]() в)
в) ![]() г)
г) ![]()


про публікацію авторської розробки
Додати розробку
