Тема уроку: Тіла обертання

Мета: Повторити, систематизувати і узагальнити знання з даної теми; показати практичне застосування знаходження об'ємів та площ поверхонь тіл обертання; звертати увагу учнів на зв'язок предмета з життям; розширювати кругозір учнів та їхню просторову уяву; вчити  орієнтуватися в нестандартних ситуаціях.

Тип уроку: узагальнення та систематизації

Обладнання: Моделі тіл обертання, посуд та предмети побуту, що мають форму тіл обертання, презентація. ХІД уроку І. Організаційний момент. 

ІІ. Оголошення теми та мети уроку.  

Вчитель.  Сьогодні у нас відбудеться незвичайний урок. Ми з Вами будем повторювати тему «Тіла обертання». Все, що ми вивчили – і правила, і формули, а також познайомимось із застосуванням цих знань у повсякденному житті.

Не даремно один з найбільш значних архітекторів двадцятого сторіччя – Ле Корбюзьє говорив: « Математика – велична споруда, створена уявленням людини для пізнання Всесвіту». 

Ми маємо можливість це показати та довести.

ІІІ. Мотивація навчальної діяльності.

Щодня Ви користуєтесь різними предметами повсякденного життя, що мають форму тіл обертання: чашки, стакани, каструльки, новорічні прикраси і т.д. Також постійно купуєте продукти у тарі такої форми, як циліндр, конус, зрізаний конус. А чи не задумувались ви над тим, чи на упаковці дійсно написана правдива вага або об’єм? І який об’єм має ваш посуд насправді? Сьогодні ми спробуємо розібратись у таких питаннях з допомогою набутих раніше нами знань.

ІV. Актуалізація опорних знань.

     Перевірка домашнього завдання.  

1. Вправа «Запитання-відповідь»

Учні обирають тему та номер запитання, відповідають на нього і передають естафету наступному учаснику.

Циліндр

1)    Що являє собою розгортка бічної поверхні циліндра?

2)    Що називається твірною циліндра?

3)    Взаємне розміщення осі циліндра з твірними.

4)    Радіус основи циліндра 8 см, чому дорівнює площа основи?

5)    Формула площі повної поверхні циліндра.

6)    Яка фігура утворюється в осьовому перерізі циліндра, якщо діаметр основи рівний висоті циліндра?

Конус

1)    Яку фігуру треба обертати і навколо чого, щоб утворився конус?

2)    Який конус називається рівностороннім?

3)    Яка фігура утворюється в осьовому перерізі зрізаного конуса?

4)    Що являє собою розгортка бічної поверхні конуса?

5)    Висота конуса це - …

6)    Висота конуса 4 см., радіус основи 3 см. Чому дорівнює твірна?

Куля

1)    Яка фігура називається кулею?

2)    За якою формулою обчислюється площа поверхні кулі?

3)    Яка січна площина має найбільшу площу?

4)    Яким є взаємне розміщення дотичної до кулі площини і радіусом кулі, проведеним в точку дотику?

5)    Як називається відрізок, який сполучає дві точки кульової поверхні і проходить через центр?

6)    Як називається частина кулі, яку відтинає від неї січна площина?

2. Вправа «Встанови відповідні пари»

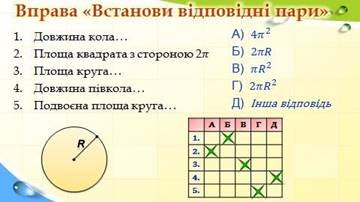
3. Вправа «Вірус» - знайди помилку

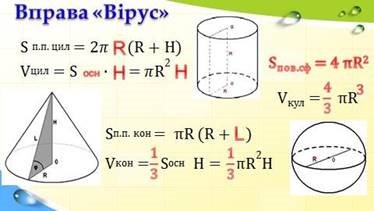
4. Тіла обертання навколо нас

(Перегляд спільної он-лайн презентації з коментарями учнів)

V. Розв’язування задач.

Розв’язування задач, маючи побутовий предмет та вимірювальні прилади.

Обчислити об’єм та площу поверхні заданого предмету.

1.     Стакан у формі циліндра (колективно)

2.     Стакан у формі зрізаного конуса. (колективно + самостійно)

3.     Вафельний конусоподібний стаканчик (самостійно)

4.     Новорічна кулька (додатково)

Учні повинні з допомогою підручних засобів зробити необхідні виміри, а потім обчислити те що необхідно за умовою.

1. Стакан (колективно) Моделюємо ситуацію:  Ви задумали приготувати смачну страву. У  рецепті вимірювання інгредієнтів записано у стаканах. Ми автоматично пам’ятаємо, який має бути стакан, але, нажаль, у вас він відсутній. Тоді можна було б використати мірну чашу, пам’ятаючи, що у стакані – 250 мл. Але її у вас також немає. У такому разі ми беремо будь-яку посудину. А як дізнатись ємкість тієї посудини? 

Проведемо дослідження: Беремо стакан, що має форму циліндра. Робимо необхідні виміри та обчислюємо необхідний об’єм.

Для здійснення вимірів можна використати нитки та лінійку. Вимірюємо висоту стакану та діаметр основи або довжину дуги кола основи.

Дано: d = 7 см

Н = 13 см Знайти: V, S_п.

Розв’язання:

D  2R  R  D:2  7:2  3,5см

V R²H (3,5)² 13159,25см³  500см³

Оскільки 1 л = 1000 см³, то 500 см³ = 500 мл S_б.п  2RН  913,14  285,74см²

S_п  2RH R²  285,74(3,5)²  285,7438,465 324,205см²

Відповідь: 500 см³, 324,205 см².

2. Стаканчик з сметани (колективно)

Моделюємо ситуацію:  Ви купуєте, наприклад, олію, сметану, сік та ін. На упаковці написано вага або літраж. Як дізнатись, що виробник написав правду?

Проведемо дослідження: Беремо стаканчик з сметани у формі зрізаного конуса. Робимо необхідні виміри та обчислюємо необхідний об’єм.

Для здійснення вимірів можна використати нитки та лінійку.  

                 ^R1                     Дано: D₁ = 9 см

           D₂ = 7 см l = 6 см

Знайти: V, S_б.п.

Розв’язання:

D  2R  R  D:2 

R₁  9:2  4,5см,R₂  7:2  3,5см

H  l² (R₂  R₁)²  6² (4,53,5)²  35  6см

V  H(R₁²  R₁ R₂  R₂² )  6((4,5)² 4,53,5(3,5)² )  289,5см³

S_б.п (R₁  R₂ )l (4,53,5)6 144см²

Відповідь: 289,5 см³, 144 см².

3. Вафельний конусоподібний стаканчик або ріжок (самостійно)

Моделюємо ситуацію:  Ви у магазині придбали вафельні ріжки, щоб їх начинити чимось смачним. В упаковці їх 24 штучки. Як визначити кількість начинки для них (об’єм)?  Яка частина вафель пішла на виготовлення таких ріжків (площа поверхні)? 

Проведемо дослідження: Беремо один ріжок. Робимо необхідні виміри та обчислюємо необхідну площу поверхні.

Для здійснення вимірів можна використати нитки та лінійку.  

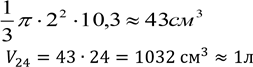Дано: D = 4 см l = 10,5 см, n=24

Знайти: V, S_п.

Розв’язання:

R  2см

                                                               H         l²  R²            (10,5)²  2² 10,3см

V  R²H 

S_б.п Rl 210,5  65,94см²

𝑆_б.п.24 = 65,94 ∙ 24 = 1582,56 см²

Відповідь: 1032 см³, 1582,56 см².

4. Новорічна кулька (додатково) Моделюємо ситуацію:  Ви у майбутньому стаєте дизайнером ялинкових прикрас (або щось інше). Вам необхідно розфарбувати 50 однакових іграшок, а для цього потрібно дізнатись кількість витратних матеріалів. Ви знаєте, що на 1 см² необхідно 0,4 г фарби.  Як Ви впораєтесь з цим завданням? Що потрібно зробити для цього?

Проведемо дослідження: Беремо одну кульку. Робимо необхідні виміри та обчислюємо необхідну площу поверхні.

Для здійснення вимірів можна використати нитки та лінійку.

Дано: С = 16 см

Знайти: V, S_б.п.

Розв’язання:

C  2R  R  C :216:2 2,7см 4        ³ 4       (2,7)³  78,732см³

V  R  

                                3              3                                                 

S_сфери  4R²  4(2,7)² 87,48см²

Відповідь: 78,732 см³, 87,48 см².

Учасники, які виконали завдання можуть розв’язувати додаткові задачі.

Додаткові задачі (дивись додаток 3)

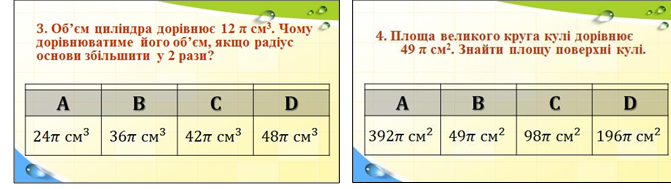
VІ. Перевірка набутих знань учнів.

Виконання тестової роботи 

Б) на планшетах, нетбуках онлайн (Тест знаходиться у блозі на сторінці даного уроку)

VІІ. Підведення підсумків уроку.

1.   Підрахунок оцінок на картках та виставлення оцінок за урок.

2.   ПОЯВА КАТЕРИНИ ОСАДЧОЇ:

-    Доброго дня, сьогодні з Вами Ірина Осадча і програма «Математичне світське життя»

-    Анрі Пуанкаре, французький математик, якось сказав: «Математика – це спосіб називати різні речі одним ім’ям». Можливість розвивати свої уміння ви сьогодні отримали. Розкажіть, що ж саме ви робили на уроці?  

-    А що означають ці слова(вислів), що написані на дошці? Як ви їх розумієте по закінченню уроку?

-    То чи потрібна Вам математика у майбутньому?

-    Чи вдалось вам відчути себе успішним на уроці?

-    А що Ви (до вчителя) скажете про сьогоднішній урок, чим він був такий корисний? 

Вчитель: На сьогоднішньому уроці ми ще раз переконалися в тому, що математичні

теорії є надійним знаряддям в розкритті таємниць природи ,життєвих  законів тощо. 

Ми досягли своєї мети, долаючи труднощі, виявляючи нетерпіння, наполегливість. На шляху нам зустрічалися явища, для розуміння і пояснення яких необхідні математичні знання. 

-    Дуже дякую Вам за чудові відповіді. З вами була Ірина Осадча і програма «Математичне світське життя». До зустрічі!

VІІІ. Рефлексія

ІХ. Домашнє завдання.

1.     Повторіть теоретичний матеріал та формули

2.     Виконайте тести 

3.     Розв’яжіть задачі 1) Паралельно осі циліндра, радіус основи якого дорівнює  см, проведено площину, що перетинає основу циліндра по хорді, яка стягує дугу, градусна міра якої дорівнює 90⁰. Знайдіть площу перерізу, якщо кут між діагоналлю перерізу та вказаною хордою дорівнює 60⁰.

2)    Площа бічної поверхні конуса дорівнює 240 𝜋 см². Знайдіть об’єм цього конуса, якщо радіус його основи дорівнює 12 см. Повторення:

3)    Відомо, що О – точка перетину діагоналей трапеції ABCD (BC||AD).

Знайдіть відрізок ВО, якщо АО : ОС = 7 : 6 і ВD  = 39 см

4)    Сторони трикутника дорівнюють відповідно 11 см, 12 см і 13 см. Знайдіть медіану, яку проведено до більшої сторони трикутника.

4.     Творче завдання:

На яку найбільшу кількість частин можуть розділити простір поверхня куба  та сфери?