Типи задач та способи їх розв'язування

Тема: Типи задач та способи їх розв'язування

(Слайд 2) Дидактична мета: ввести поняття: арифметичний та алгебраїчний способи розв'язування задач; дати класифікацію задач: задачі на вартість, задачі на роботу, задачі на рух, геометричні задачі;

Розвиваюча мета: формувати вміння раціонального вибору способу розв'язування задач; розвивати логічне мислення, навики перенесення раніше набутих знань на вивчення нового матеріалу, рефлексивну компетентність;

Виховна мета: виховувати відповідальність за доручену справу; формувати соціальні компетенції;

Тип уроку: урок засвоєння і вдосконалення навичок і вмінь;

Обладнання: мультимедійна дошка, проектор.

Хід уроку

І. Оголошення  теми й мети уроку

ІІ. Актуалізація опорних знань

1. Знайти ціну цукерок, якщо:

а) за 2 кг заплатили 40 грн.

б) за 3 кг заплатили 63 грн.

в) за 3 кг заплатили х грн.

2. Знайти швидкість автобуса, якщо:

а) за 2 год він проїжджає 130 км

б) за 6 год він проїжджає 240 км

в) за 4 год він проїжджає х км

3. Знайти швидкість руху човна за течією річки і проти течії, якщо:

а) власна швидкість човна – 12 км/год, а швидкість течії - 4 км/год

б) власна швидкість човна – 15 км/год, а швидкість течії – 2 км/год

в) власна швидкість човна – 15 км/год, а швидкість течії – х км/год

Продуктивність праці – це обсяг продукції, виготовленої за деякий проміжок часу

4. Знайти продуктивність праці токаря, якщо:

а) за 2 год він виготує 8 деталей

б) за 4 год він виготує 40 деталей

в) за 4 год він виготує х деталей

ІІІ. Сприйняття та усвідомлення нового матеріалу. Мотивація навчальної діяльності.

Вчитель: Ми повторили з вами залежність між величинами, так як сьогодні будемо розглядати задачі, де мова йтиме про одну, дві або три величини. Кожну задачу можна розв’язати за діями, як це робили раніше. Такий спосіб називають арифметичним. Але можна за умовою задачі скласти рівняння та розв’язати його. Такий спосіб називається алгебраїчним.

Знаючи різні способи розв'язування задач, завжди можна обрати найлегший, найкоротший і найраціональніший. В майбутньому це може допомогти в організації власного бізнесу, своєї справи, і навіть допомогти в формуванні бюджету сім’ї.

Учні-консультанти презентують вам по два способи розв'язування задачі і ви будете вирішувати, яким із них краще скористатися для розв'язування певної задачі. Слухаємо уважно, задаємо запитання, щоб можна було навчитися розв’язувати задачі самостійно та обрати кращий спосіб розв’язання.

Кожну задачу пояснюють по 2 учні-консультанти, що підготувалися заздалегідь, а потім пропонується задача для розв'язування в класі

Задачі для розв’язування в класі:

1. Розв'язати задачу (Слайд 3)

У Буратіно було 74 сольдо. Після того, як він купив собі підручники для школи, тато Карло дав йому 25 сольдо. Тоді у Буратіно стало 68 сольдо. Скільки сольдо витратив Буратіно на підручники?

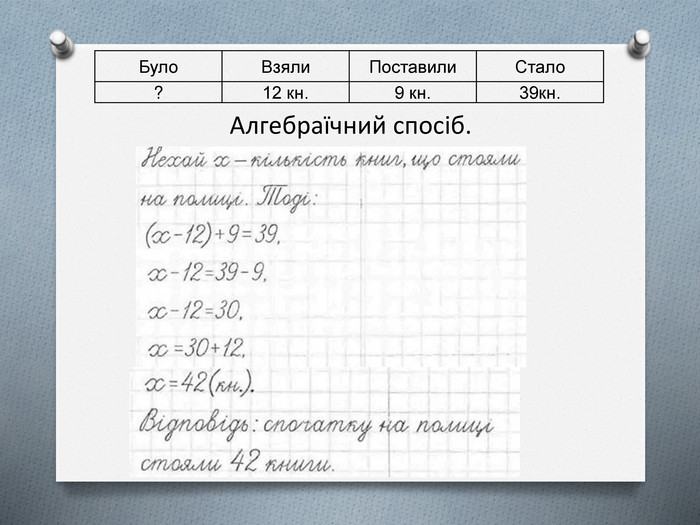
Розв’язання (Слайд 4-5 )

Нехай Буратіно витратив на підручники х сольдо, тоді

(74 – х) + 25 = 68

74 – х = 68 – 25

74 – х = 43

х = 74 – 43

х =31

Відповідь: Буратіно витратив на підручники 31 сольдо.

2. Розв'язати задачу (Слайд 6):

З вершини прямого кута проведено промінь так, що він ділить прямий кут на два кути, один з яких більший за другий на 20 . Знайти величину кожного з утворених кутів.

Розв’язання (Слайд 7)

Прямий кут дорівнює 90˚ . Один з утворених кутів х, а другий х + 20˚.

х + х+ 20˚ = 90˚

2х = 90˚ – 20˚

2х = 70˚

х = 70˚ : 2

х = 35˚

35˚ + 20˚ = 55˚

Відповідь: один з кутів дорівнює 35˚ , а другий 55˚ .

3. Розв'язати задачу (Слайд 8):

 За 5 зошитів і 3 ручки заплатили 17 грн. 50 коп. Скільки коштує 1 зошит і 1 ручка, якщо зошит дешевший від ручки на 50 коп. ?

Розв’язання (Слайд 9-10)

1 зошит коштує х коп., а 1 ручка (х + 50) коп.

5 зошитів коштує 5х грн., а 3 ручки 3(х + 50) коп.

Вся покупка 17 грн. 50 коп. = 1750 коп.

Маємо рівняння:

5х + 3(х + 50) = 1750

5х + 3х + 150 = 1750

8х = 1750 – 150

8х = 1600

х = 1600 : 8

х = 200

1 зошит коштує 200 коп.=2 грн.

1 ручка коштує 200+50=250 коп.=2 грн. 50 коп.

Відповідь: 2 грн., 2 грн. 50 коп.

4. Розв'язати задачу (Слайд 11)

У фруктовому саду необхідно посадити 12 дерев. Один робітник може виконати завдання за 6 год. Знайти час, необхідний для виконання цього завдання другим робітником, якщо за годину він саджає на 1 дерево більше, ніж перший робітник

Розв’язання (Слайд 12)

1) 12 : 6 = 2 (д) – продуктивність І робітника;

2) 2 + 1 = 3 (д) – продуктивність ІІ робітника;

3) 12 : 3 = 4 (год) – потрібно ІІ робітнику

Відповідь: 4 год.

5. Розв'язати задачу (Слайд 13):

Автомобілі виїхали одночасно із пункту А в протилежних напрямках. Перший автомобіль їхав зі швидкість 70 км/год, а другий – зі швидкість, на 10 км/год меншою, ніж перший автомобіль. На якій відстані один від одного будуть знаходиться автомобілі через 2 год після виїзду?

Розв'язання (Слайд 14-15)

1) 70 – 10 = 60 (км/год) – швидкість другого автомобіля;

2) 70 2 = 140 (км) – проїхав перший автомобіль;

3) 602 = 120 (км) – проїхав другий автомобіль;

4) 140 + 120 = 260 (км) – відстань між автомобілями;

Відповідь: 260 км.

6. Розв'язати задачу (Слайд 16):

За 5 зошитів і 3 ручки заплатили 17 грн. 50 коп. Скільки коштує 1 зошит і 1 ручка, якщо зошит дешевший від ручки на 50 коп. ?

Розв'язання (Слайд 17)

1 зошит коштує х коп., а 1 ручка (х + 50) коп.

5 зошитів коштує 5х грн., а 3 ручки 3(х + 50) коп.

Вся покупка 17 грн. 50 коп. = 1750 коп.

Маємо рівняння:

5х + 3(х + 50) = 1750

5х + 3х + 150 = 1750

8х = 1750 – 150

8х = 1600

х = 1600 : 8

х = 200

1 зошит коштує 200 коп.=2 грн.

1 ручка коштує 200+50=250 коп.=2 грн. 50 коп.

Відповідь: 2 грн., 2 грн. 50 коп.

ІV. Підведення підсумків

Що нового з'явилося у вашому арсеналі знань про розв'язування задач?

Чи можна однозначно виділити, який спосіб розв'язування задач кращий?

Щоб розв’язувати задачі, треба знати…

V. Домашнє завдання (Слайд 18)

Розв'язати задачі:

1. На скільки днів шкільній їдальні вистачить 800 л молока, якщо хлопчики за 8 днів випивають 960 л молока, а дівчатка за 6 днів – 480л?

2. З вершини розгорнутого кута проведено промінь так, що він ділить розгорнутий кут на два кути, один з яких менший від другого на 50 . Знайти величину кожного з утворених кутів.