Тотожні вирази. Тотожність. Тотожні перетворення виразів

Тема. Тотожні вирази. Тотожність. Тотожні перетворення виразів

Мета: систематизувати й узагальнити знання учнів про перетворення виразів, набуті учнями в 5-6 класах; поглибити знання про види виразів (тотожні вирази); оволодіти новою термінологією.

Тип уроку: засвоєння знань.

Хід уроку

І. Перевірка домашнього завдання

№ 2 — зібравши зошити, перевіряємо якість виконання завдань.

Розв'язання і відповіді:

1) має зміст при будь-якому значенні а, бо це — цілий вираз;

2) має зміст при всіх а, окрім а = 3,5, бо при а = 3,5 дільник 2а – 7 дорівнює 0;

3) має зміст при будь-якому значенні а, бо, хоча вираз і дробовий, дільник а² +4 > 0 (тобто не дорівнює нулю) при будь-якому а;

4) має зміст при всіх а, окрім а = 0, бо при а = 0 знаменник (дільник) 9а = 0.

II. Актуалізація опорних знань

Ігровий момент. Гра в «Шаради» (або «німий» диктант)

Технологія проведення

На дошці записано кілька виразів, наприклад:

1) 5 · 2 – 3 : 1,5; 2) 5а – 3 : с; 3) 5а – .

Учитель вказує на певний запис (вираз), а завдання учнів — згадати Назву і якомога більше відомостей про цей вираз.

Наприклад: 1) 5 · 2 – 3 : 1,5 – числовий вираз; порядок дій (1) множення; 2) ділення; 3) віднімання); значення цього числового виразу 8; словами читається так: різниця добутку чисел 5 і 2 і частки чисел 3 і 1,5 тощо.

III. Робота з випереджальним домашнім завданням

На дошці записано умову № 1 домашнього завдання (див. попередній урок).

Учні отримують для самостійної роботи за результатами виконання випереджальне домашнє завдання.

Таблиці для заповнення (додаток)

Після самостійного виконання роботи виконуємо перевірку та корек­цію отриманих спостережень, і, якщо робота пройде успішно, учні самі роблять висновок, що звучить приблизно так:

Два виразі (зі змінними) можуть набувати або рівних, або нерівних значень при різних значеннях змінних: деякі пари виразів (зі змінними) набувають рівних відповідних значень за будь-яких значень змінних, що входять до їх складу, а деякі пари виразів не відповідають цій умові.

Після формулювання цієї тези доречно дати зрозуміти учням, що саме перший вид виразів часто розглядають у математиці, і тому про перший вид виразів піде мова на уроці. Далі формулюється тема й мета уроку.

IV. Засвоєння знань

 Тотожні перетворення виразів є одним з найважливіших розділів шкільної алгебри. Вивчення їх пронизує весь курс шкільної алгеб­ри, хоча основу для формування оперативних навичок виконання тотожних перетворень було закладено ще в 5—6 класах. І хоча рівень формально-оперативних умінь залишається таким самим, учні ма­ють можливість піднятися на вищий щабель в оволодінні теорією — уводяться відповідні терміни: тотожно рівні вирази; тотожні пере­творення виразів; тотожність. Увага учнів акцентується на тому, що основою тотожних перетворень є властивості дій над числами (буквений запис яких є, у свою чергу, також тотожностями), і з цих позицій розглядаються ті перетворення алгебраїчних виразів, що вже відомі учням (зведення подібних доданків; розкриття дужок).

Отже, на основі розібраного випереджального домашнього завдання спочатку формулюємо поняття тотожно рівних виразів; наступним кро­ком уводимо поняття тотожного перетворення виразів. З поняттям тотожно рівних виразів пов'язано й поняття тотожності. Якщо ліва й права час­тини деякої рівності є рівними виразами, то така рівність правильна за будь-яких значень змінних, що входять до її складу. Рівність, правильна за будь-яких значень змінних, називається тотожністю.

На цьому й завершується викладання змісту теоретичного матеріалу уроку.

V. Закріплення знань

 Основна мста уроку — закріпити термінологію, тому виконанню завдань на закріплення термінології приділяється особлива увага.

Виконання усних вправ

1. Чи є тотожно рівними вирази:

1) 5 + 6x та 6х + 5; 2) а · 5b та 5аb; 3) а – b та b – а?

2. Чи є тотожністю рівність:

1) ab + 2 = 2 + ab; б) a – 1 = - 1 + а; в) 2(a – 3) = 2а – 3?

3. Назвіть кілька виразів, що тотожно рівні виразу х + 4х.
4. Поясніть, на основі яких властивостей дій здійснено такі тотожні пере­творення:

-2b – (a – 3b) + 5a = -2b – a + 3b + 5a = -2b + 3b – a + 5a =

= (-2 + 3)b + (-1 + 5)а = b + 4а.

5. Спростіть вираз (виконайте тотожні перетворення виразів):
   а) -7 + 4а – 3а; б) 4а · 5b; в) 5х + (2 – х).

Виконання письмових вправ

1. Перетворіть вираз у тотожно рівний йому, використовуючи відповідні
   властивості дій над числами:

1) -6,2a · 5;    2) 0,3х · (-12у);   3) -23 · (2a – 3b + 1);

4) 1,5(-3x + 4y – 5z);   5) 13a + 7b – 2a – b; 6) -5,1a – 4b – 4,9a + b.

2. Виконайте тотожні перетворення виразів:

1) x + (a – b) – (c + d);  2) a + (b – (c – d));  3) (х – 1) + (12 – 7,5x);

4) 4(6 – 5х) + 17х – 10;  5) 0,2(3a – 1) + 0,3 – 0,6а;  6) -2,6(5 – с) – с + 8.

3. Чи є тотожністю рівність (поясніть, використовуючи дії над числами):

1) ab + 16c = 16c + ab;  2) 5(b + c) = 5b + 5c;

3) a · 25b = 25ab;   4) (x – x)a = 0?

4. Запишіть у вигляді рівності такі твердження:

1. добуток будь-якого числа й нуля дорівнює нулю;
2. сума двох протилежних чисел дорівнює нулю;
3. добуток двох чисел дорівнює добутку чисел, їм протилежних;
4. квадрат будь-якого числа дорівнює квадрату числа, йому протилежного. Чи є записані рівності тотожностями? Чому?

VI. Підсумок уроку

1. Які вирази називаються тотожно рівними?
2. Наведіть приклад тотожно рівних виразів:

а) що містять одну змінну; б) що мають дві змінні.

3. Яка рівність називається тотожністю?

VII. Домашнє завдання

№ 1. Чи є вирази тотожно рівними:

1) 2х + 3у і 3у + 2х;   2) 2х + 14 і 2(х + 7);

3) (а + b) · 0 і а + b;  4) (а + b) · 1 і а + b?

№ 2. Перетворіть вираз у тотожно рівний, використовуючи тотожні перетворення (властивості дій над числами, правила розкриття дужок та зведення подібних доданків):

1) -0,1b · (-2,3с);  2) 2,5(4х – 6y – 2);  3) 3,5b – 2,4с – 0,6с – 0,7b;

4) b – (4 – 2b) + (3b – 1);   5) 0,9(2b – 1) – 0,5b + 1.

№ 3. Випереджальне домашнє завдання. Обчисліть значення виразів:

1) 3 · 4,9 + 4,9 · 6; 2) .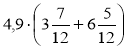

Порівняйте (за алгоритмом) і з'ясуйте,

а) що є спільним для цих виразів; б) чим відрізняються ці вирази;

в) які висновки з порівняння можна зробити?