Тотожні вирази. Тотожні перетворення виразів. Тотожності

Тема. Тотожні вирази. Тотожні перетворення виразів. Тотожності

Мета: закріпити знання учнів про основні поняття, вивчені на попе­редньому уроці; відпрацювати навички .володіння термінологією; вдоско­налити вміння складати вирази за умовою, виконувати тотожні перетво­рення виразів, обчислювальні навички.

Тип уроку: застосування знань, засвоєння навичок.

Хід уроку

І. Перевірка домашнього завдання. Актуалізація опорних знань

 Ступінь розуміння термінології перевіряємо під час самостійної ро­боти (вправи на дописування).

Для самостійного виконання (з наступною перевіркою)

1. Два вирази називаються тотожно... якщо при... значеннях букв... зна­чення цих виразів...
2. Якщо два тотожно рівні... сполучити знаком... дістанемо рівність, що називається...
3. Записані нижче рівняння є тотожностями. Заповніть пропуски:

a + b = b + ...; ab = b...; (a + b) +c =...+ (b + c); (a...)c = a(b...); a(...+...) = ab+ac.

4. Якщо один з виразів замінити тотожно рівним йому виразом, то така
   заміна називається... перетворенням.

5.* Із запропонованих слів (словосполучень) утворіть пари, об'єднані пев­ною (однією) логікою (змістом): 1) вирази; 2) тотожність; 3) заміна; 4) тотожно рівні; 5) рівність; 6) тотожне перетворення. Поясніть логіку.

II. Робота з випереджальним домашнім завданням. Обґрунтування технології роботи з обчислення значень виразів зі змінними

На дошці записано вирази: 1) 3 · 4,9 + 4,9 · 6; 2) .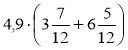

Учні презентують свою роботу з обчислення і порівняння відповідей і способів дій (спільне, різне, висновки) і коригують свої міркування (правильність обчислень, спосіб виконання, порядок дій). Після проведе­ного обговорення підбиваємо підсумки.

Нам відомо, що в подібних випадках можна замінювати «більш склад­ний» вираз на «більш простий», який має те ж саме значення, і виконува­ти обчислення простіше (див. урок 1).

Виникає запитання: а чи не можна так само робити із буквеними ви­разами, тобто «більш складний» вираз замінити «більш простим», але щоб вони мали однакове значення, тобто були тотожно рівними, і потім об­числювати значення «більш простого» (спрощеного) виразу.

III. Засвоєння навичок

Виконання усних вправ

1. Замініть вираз тотожно рівним:

(2a – 1)b; a · (-b); 4(a – 2b); -4b + 4a – 4b; a – (b +37); 3x – 3y.

2. Відомо, що при деяких значеннях а та b вираз 4(а – 2b) дорівнює 42. Яке
   значення при цьому має вираз:

1) 4a – 8b;  2) -4(2b – a);  3) -4b + 4a – 4b?

3. Знайдіть значення виразу (a + b) + (a + b) + (a + b) + (a + b), якщо:

1) a = 41; b= -16;   2) a + b = 7.

4. Різниця чисел a та b дорівнює 37. Чому дорівнює різниця a – (b + 37)?

Виконання письмових вправ

1. Спростіть вираз та знайдіть його значення:
   1) 0,7(а – 10) + a – 5 при а = 3;  2) -2,5b - (11 – 1,5b) + b при b = 0,2;

3) 2x – 3(1 – y) + 4y при х = -2; у = 5; 4) 5(-4х + 0,6) + 17,5х – при х = 0,8;

5) 25х – 4(5х – 3у) – 2(5 + 3х – у) при х = -7,6; у = 0,76.

2. Ширина прямокутника а см, а довжина на 3 см більша. Запишіть у вигляді виразу периметр прямокутника. Знайдіть значення цього ви­разу, якщо а = 0,02 м.
3. Перший лижник пробіг а м, другий — на b м менше, а третій 1,2 км. На скільки метрів менше пробіг другий лижник, ніж перший і третій ра­зом? Запишіть відповідний вираз зі змінними. Обчисліть значення цьо­го виразу, якщо а = 1100 (м), b = 300 (м).
4. З міста А до міста В виїхав мотоцикліст і рухався зі швидкістю 54 км/год. Через 0,5 год назустріч йому з міста В виїхав автомобіль і, проїхавши t год, зустрів мотоцикліста. Запишіть у вигляді виразу відстань між містами, якщо швидкість автомобіля 72 км/год. Обчисліть значення цього виразу, якщо t = 3.

 Дуже важливо акцентувати увагу учнів на тому, що навіть, якщо в умові завдання безпосередньо не сказано про попереднє тотожне перетворення виразу, в будь-якому разі, перш ніж обчислювати, на­магаємось спростити (або перетворити) відповідно до умови.

5*. Двозначне число, яке має а десятків та b одиниць, позначають через (позиційний запис числа). Отже, = 10а + b. Запишіть у вигляді виразу + і спростіть його.

IV. Підсумки уроку. Рефлексія

Використавши знання й уміння, набуті на уроці, складіть алгоритм розв'я­зання завдання: «Обчислити значення виразу... при... (значенні змінної)».

V. Домашнє завдання

№ 1. Спростіть вираз та запишіть його значення:

1) 6 + 3(2а – 4) – 8а при а = -1; 2) 3(а + 6) – (а – 3b) – 4b при а = 3; b = -3.

№ 2. Складіть вираз за умовою задачі та знайдіть його значення при заданих значеннях змінних:

1. Один робітник виготовляє за годину с деталей, а другий — на дві деталі менше. Скільки деталей виготовлять обидва робітники за 8 год. Обчисліть при  с = 10.
2. На одній полиці стоїть х книжок, на другій — удвічі більше. З першої полиці забрали 10 книжок, а на другу поставили 3 книжки. Якою стала загальна кількість книжок на полицях? Обчисліть при х = 21. Чи можна обчислити при х = 9?

№ 3. Випереджальне домашнє завдання. Спростіть вирази, виконавши тотожні перетворення: 1) х(у – 1) – 3у і 2) у(х – 3) – 2х.

Порівняйте дані й здобуті вирази. Що можна сказати, виходячи з цьо­го, про дані два вирази?