Вирази зі змінними. Тотожності

Тема. Вирази зі змінними. Тотожності

Мета: домогтися свідомого розуміння суті поняття «тотожність» і спо­собів доведення тотожності шляхом тотожних перетворень та оволодіння прийомами доведення тотожностей, використання цих прийомів для розв'язування вправ на доведення тотожностей різного рівня складності.

Тип уроку: засвоєння навичок.

Хід уроку

І. Перевірка домашнього завдання

Вправи № 1-2 або перевіряємо усно, або учні заповнюють листки відповідей:

II. Робота з випереджальним домашнім завданням

На дошці записано: 1) х(у – 2) – 3у; у(х – 3) – 2х.

• Які вирази дістали після виконання тотожних перетворень?
• Чи є вирази «однаковими»? Чим відрізняються?
• Що маємо спільного?
• Який би знак ви поставили між виразами?
• Які висновки можна зробити?

Залежно від того, як було здійснено порівняння, учні можуть сформу­лювати різні висновки, але, напевно, серед них будуть і такі (дуже важли­во, щоб вони прозвучали й на них звернули увагу):

1.   Тотожно рівні вирази не завжди є однаковими (тотожність не є «одна­ковість» або не тільки «однаковість» — це більш широке поняття).
2.   Спосіб утворення тотожностей такий: між двома тотожно рівними ви­разами ставимо знак «=».
3.   Щоб перевірити, чи є два вирази тотожно рівними, достатньо тотожно перетворити кожний з них і порівняти здобуті вирази. Якщо вони однакові або, напевно, рівні (виходячи з відомих тотожностей: власти­востей дій над числами), то й дані два вирази є тотожно рівними, тобто рівність, що складається з цих двох виразів, є тотожністю.

III. Усвідомлення матеріалу; алгоритмізація способів дій

 Вступна бесіда. Знайомство учнів зі змістом поняття «доведення» та алгоритмом доведення (додаток).

Після цієї бесіди учні працюють з алгоритмом (алгоритми роздаються учням).

Завдання 1. Доведіть тотожність (а + b) – (а – b) = 2b.

 Важливо спонукати учнів до самостійної діяльності, тому, пояснив­ши кожний крок алгоритму, вчитель пропонує учням самостійно ви­конати доведення. Після виконання цієї роботи — обов'язкова корекція, тому для більш швидкого виконання корекції бажано, щоб учні записували свої дії поетапно (як про це сказано в алгоритмі):

Після обговорення результатів і корекції виконаних завдань переходи­мо до наступного етапу уроку.

IV. Застосування знань, умінь та навичок

Не забуваємо про порівняння завдань і класифікацію, яка допомагає визначитися з тим, як може змінитися спосіб застосування одного й того самого алгоритму (в одних тотожностях треба перетворювати обидві час­тини, в інших одну перетворити до виду іншої частини тотожності). Звер­таємо увагу й на вправи високого рівня складності, що передбачають спо­чатку складання тотожності за умовою завдання, а вже після цього — доведення цієї тотожності.

Виконання письмових вправ

1. Доведіть тотожність:

1) 2b(-4) + 8b – 4 = -4;   2) 2x – 1 – 5(1 – 2х) = 12х – 6;

3) a – (4a – 3b) = 3(b – a); 4) 2c = 12c – 5(2c + 3) + 15.

2. Доведіть тотожність:

1) 2(a + b + c) – (a + b + c) – (a – b + c) = 2(b + c);

2) 28 + 2(2(2(b – 2) – 2) – 2) = 8b.

3. Нехай тіл — деякі натуральні числа. Доведіть, що:

а) різниця чисел 11т + 3n і 7т + 7n  ділиться на 4;

б) сума чисел 10m + 3n + 2 і 2т + 5п – 2 ділиться на 4.

 Розв'язуванню вправ №3, 4 повинні передувати вправи, що актуалі­зують знання учнів щодо змісту поняття подільності чисел (напри­клад, ціле число а ділиться на ціле b, якщо існує ціле число с таке, що а = bc. Тоді якщо число а ділиться на 4, то це означає, що а = 4с, де с — ціле число). Тоді п. 1 з алгоритму доведення реалізуємо так:

3. Доведіть, що (11т + 3n) – (7т + 7n) = 4с, де с — ціле число і т. д.

4. Пригадайте, що означає а та b y запису .
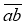   Як ви будете розуміти запис ? ?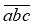
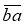   1. Доведіть, що сума 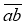+ ділиться на 11.
   2. Доведіть, що різниця числа 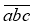і сума його цифр ділиться на 9.

5*. (Додатково, на повторення). Знайдіть значення виразу

.

V. Підсумок уроку. Рефлексія

Серед списку математичних термінів виберіть ті, що стосуються теми уроку: числовий вираз; корінь рівняння; тотожність; тотожно рівні; вираз зі змінними; рівносильні; числове значення виразу; доведення; перетво­рення; цілий вираз.

VI. Домашнє завдання

№ 1. Повторити вивчені алгоритми розв'язання завдань:

1. Обчислити значення числового виразу.
2. Обчислити значення буквеного виразу (виразу зі змінними).
3. Як знайти значення змінних, при яких вираз зі змінними має зміст.
4. Виконати тотожні перетворення виразів.
5. Довести тотожність.

№ 2. Використовуючи текст підручника, підібрати й розв'язати зав­дання (або скласти самим) на застосування названих алгоритмів.

Додаток

Алгоритм доведення

1. Встанови й сформулюй проблему (твердження), яку треба довести.
2. Дай означення поняттям, за допомогою яких буде здійснюватись доведення.
3. Добери ґрунтовні аргументи.
4. Визнач спосіб і логіку доведення.
5. Зроби висновок.

Аргументи (підстави) — судження, істинність яких перевірена й дове­дена (практикою). Головною характеристикою є істинність, тобто відпо­відність дійсності.