"Третя ознака рівності трикутників."

Тема: Третя ознака рівності трикутників

Мета:

• домогтися розуміння учнями змісту третьої ознаки рівності трикутників та ідеї її доведення; формувати первинні вміння застосовувати третю ознаку рівності трикутників для розв’язування задач;
• розвивати логічне мислення, пам’ять, увагу, уяву, культуру математичного мовлення та письма;
• виховувати наполегливість, старанність у навчанні.

Тип уроку: урок засвоєння нових знань та вмінь.

Хід уроку

І. Організаційний момент (1-2 хв)

Привітання. Перевірка присутності.

ІІ. Перевірка домашнього завдання (2-3 хв)

Перевіряю наявність виконаного домашнього завдання. З’ясовую, які завдання викликали в учнів труднощі та відповідаю на запитання.

ІІІ. Актуалізація опорних знань. (3-4 хв)

Фронтальне опитування

1. Які фігури називають рівними?

(Рівними називають фігури, які можна сумістити рухом (накладанням).)

2. Сформулюйте першу ознаку рівності трикутників.

(Якщо дві сторони і кут між ними одного трикутника дорівнюють відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні.)

3. Сформулюйте другу ознаку рівності трикутників.

(Якщо сторона і прилеглі до неї кути одного трикутника дорівнюють відповідно стороні й прилеглим до неї кутам другого трикутника, то такі трикутники рівні.)

4. Чи можуть сторони трикутника бути довільними відрізками?

(Ні. У трикутнику одна сторона повинна бути меншою від суми двох інших сторін)

5. Скільки трикутників із заданими довжинами трьох сторін можна побудувати? Якими між собою будуть побудовані трикутники і чому?

(Таких трикутників можна побудувати безліч. Між собою вони будуть рівними, бо, по-перше: їх можна сумістити рухом, і по-друге: їхні відповідні сторони рівні.)

IV. Повідомлення теми і мети уроку. Мотивація навчальної діяльності. (2 хв)

Сьогодні ми з вами розглянемо і доведемо третю ознаку рівності трикутників – за трьома сторонами, а також будемо вчитися застосовувати третю ознаку рівності трикутників для розв’язування задач.

Тема нашого уроку: Третя ознака рівності трикутників.

V. Пояснення нового матеріалу. (15-20 хв)

Теорема 14 (третя ознака рівності трикутників): Якщо три сторони одного трикутника дорівнюють відповідно трьом сторонам другого трикутника, то такі трикутники рівні.

Доведення:

Нехай у трикутників АВС і А₁В₁С₁ АВ = А₁В₁, АС = А₁С₁ і ВС = В₁С₁ (мал. 2). Доведемо, що ∆АВС = ∆А₁В₁С₁.

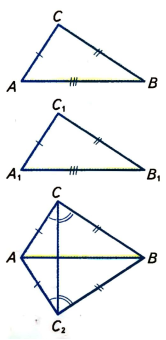      Прикладемо трикутник А₁В₁С₁  до трикутника АВС так, щоб вершина А₁ сумістилася з А, В₁ – з В, а С₁ і С виявилися по різні боки від прямої АВ. Тоді ∆ А₁В₁С₁ займе положення ∆АВС₂. Провівши відрізок СС₂, одержимо рівнобедрені трикутники САС₂ і СВС₂, бо АС = АС₂ і ВС = ВС₂. У цих трикутників кути при основах рівні: АСС₂ = АС₂С,  ВСС₂ = ВС₂С. Отже, рівні також кути АСВ і АС₂В. Тому за двома сторонами і кутом між ними ∆АВС = ∆АВС₂.                                                 

За побудовою ∆АВС₂ = ∆А₁В₁С₁. Таким чином, ∆АВС = ∆А₁В₁С₁, що і треба було довести.

На ознаки рівності трикутників згодом доведеться посилатися досить часто. Щоб не сплутати, яку з них названо першою, яку другою, а яку третьою їх краще розрізняти за змістом, говорити про ознаку рівності трикутників:

•   за двома сторонами і кутом між ними;
•   за стороною і двома прилеглими кутами;
•   за трьома сторонами.

В усіх трьох ознаках рівність трикутників випливає з рівності трьох пар відповідних елементів. І це не випадково: як правило, трикутник можна задати (побудувати) саме за трьома елементами, але не довільними, а такими, що визначають єдиний трикутник. Наприклад, трикутник можна однозначно задати довжинами трьох його сторін. Однак, наприклад, градусні міри трьох кутів не задають трикутник однозначно.

Трикутник визначається (задається) однозначно:

1. двома сторонами і кутом між ними;
2. стороною і двома прилеглими кутами (при чому кутами, сума яких менша від 180^о);
3. трьома сторонами (при чому кожна із сторін має бути меншою від суми двох інших.)

VI. Закріплення нового матеріалу. (10-15 хв)

Виконайте усно

№ 419

∆АВС = ∆КРТ. Знайдіть периметр трикутника КРТ, якщо:

а) кожна сторона ∆АВС дорівнює 5 см;

б) АВ = ВС = 3 дм, АС = 4 дм.

(а. Р_∆АВС = 5 + 5 + 5 = 15 (см). Оскільки ∆АВС = ∆КРТ, то і їх периметри рівні. Отже, Р_∆КРТ = 15 см;

б. Оскільки трикутники АВС і КРТ рівні, то їх відповідні сторони також рівні. Отже, Р_∆КРТ = 3 + 3 + 4 = 10 (см).)

 

Робота біля дошки і в зошитах

1. Точки B i D лежать по різні боки від прямої АС (мал. 3). Відомо, що АВ = AD і ВС = СD. Довести, що В = D.

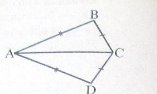
Малюнок 3

(Доведення:

У трикутниках АВС і  ADC АВ = AD, BC = CD за умовою, сторона АС – спільна. Отже, ∆АВС = ∆ADC за третьою ознакою рівності трикутників.

З рівності ∆АВС = ∆ADC, за означенням рівних трикутників випливає рівність кутів В і D.)

№ 425

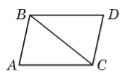Прикладаючи два різні трикутники з кутами 30° і 70°рівними сторонами, можна утворити кілька різних чотирикутників. Зобразіть їх на малюнку, визначте кути утворених чотирикутників

1) Нехай в ∆АВС АВС = 70°, АСВ = 30°, а в ∆ВDC DBC = 30°,

DCB = 70°. Знайдемо кути чотирикутника.

А = D = 180° - (70° + 30°) = 80° (як кути ∆АВС й ∆ВDC).

ABD = ABD + CBD, ABD = 30° + 70° = 100°,

ACD = ACB + DCD, ACD = 30° + 70° = 100°.

Відповідь: 100°, 100°, 80°, 80°.

VII. Підсумок уроку. (2-3 хв)

1. Сформулюйте третю ознаку рівності трикутників (Якщо три сторони одного трикутника дорівнюють відповідно трьом сторонам другого трикутника, то такі трикутники рівні).

2. Сформулюйте першу і другу ознаки рівності трикутників.(І - якщо дві сторони і кут між ними одного трикутника дорівнюються відповідно двом сторонам і куту між ними другого трикутника, то такі трикутники рівні. ІІ - якщо сторона і прилеглі до неї кути одного трикутника дорівнюються відповідно стороні й прилеглим до неї кутам другого трикутника, то такі трикутники рівні).

VIII. Повідомлення домашнього завдання. (1-2 хв)

IX. Оцінювання і мотивація. (1-2 хв)

Виставляю оцінки і мотивую учнів.