Тригонометричні функції. Властивості функції у=sin x

Тема: Тригонометричні функції. Властивості функції у=sin x.

                Побудова її графіка. Дослідження властивостей синусоїди
                на основі динамічної програми.

     Мета: Формування знань учнів про поняття синуса, співвідношеннями між кутами, утвореними радіусами кола та ординатами точок кола, дослідження властивостей синуса для довільного значення кута на основі авторської програми Prot2.exe. Вироблення навичок та вмінь самостійного застосування властивостей синуса при розв’язуванні задач і вправ. Виховання логічного мислення, розвиток абстракції, творчості, інтелектуального потенціалу.

Хід уроку

І.  Організаційний момент.

Оголошення теми, мети та завдань уроку. Розміщення учнів для найкращого сприйняття відеоматеріалів, виконання творчих завдань.

ІІ. Актуалізація опорних знань учнів.

Фронтальна бесіда на повторення. Виконання письмових завдань, індивідуальних завдань.             Завдання творчим групам:

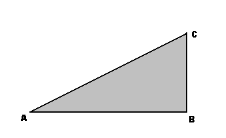
Рис. 2.18. Рисунок до індивідуального завдання

В прямокутному ∆АВС(рис. 2.18) катети а). АВ = 8см, ВС = 6см;

                                                                      б). АВ=10дм, ВС=7,5дм;

                                                                      в). АВ=12м, ВС=9м.

Знайти гіпотенузу АС, sin A.

Порівнюємо результати. Очікувані відповіді: 10 см, 12,5 дм, 15м, sin A=0,8.

Питання: чому для різних трикутників значення синуса те ж саме? що потрібно змінити, щоб змінилося значення синуса? чи можливо з цього завдання дати поняття синуса від’ємного кута, кута більшого за 180°?  

Очікувані відповіді: ці трикутники подібні, тому мають рівні кути, значення синуса не залежить від розмірів трикутника, а залежить від величини кута А; значення синуса зміниться, якщо збільшити або зменшити кут А; ні, тому що згідно аксіом планіметрії градусна міра кута – величина додатна, сума кутів трикутника – 180°. Яка геометрична фігура чи її частина дозволяє розширити поняття синуса чи косинуса для кутів від 0° до 180°? Очікувана відповідь: Нехай