Тригонометричні нерівності. Алгебра 10 клас.

Тригонометричні нерівності

Блез Паскаль1623-1662 Математика настільки серйозний предмет, що не треба пропускати можливості зробити його цікавішим.

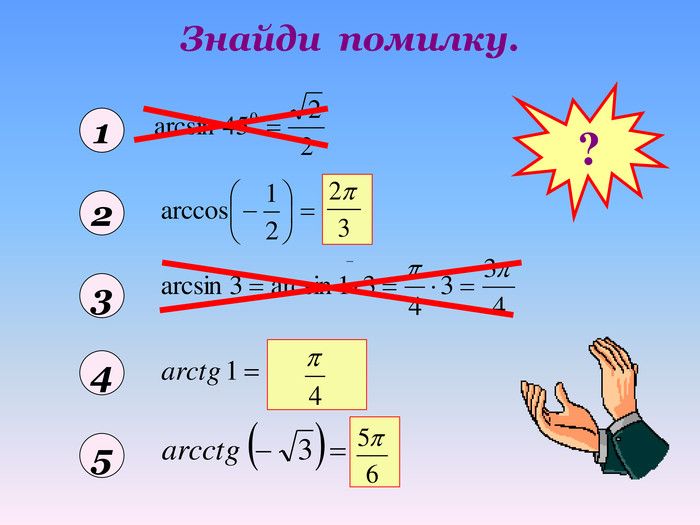
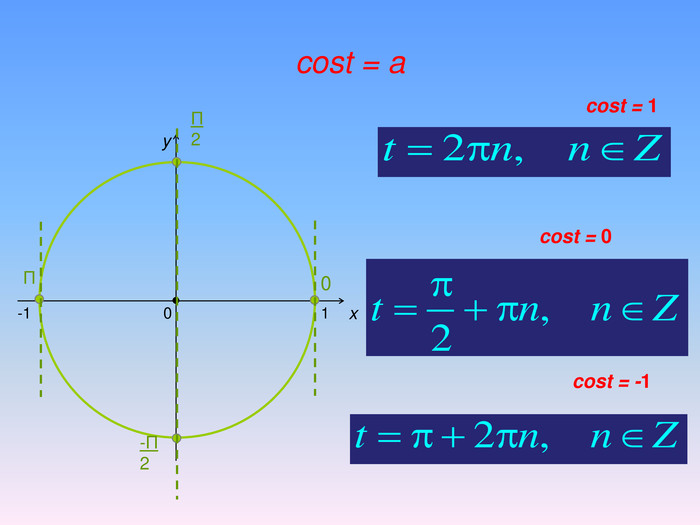
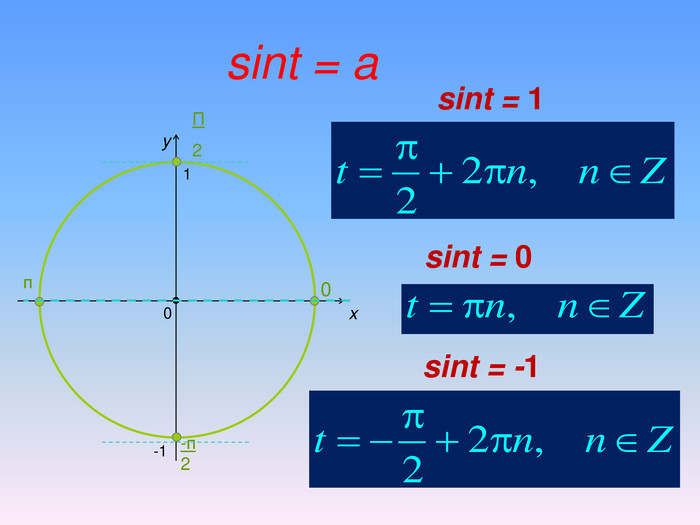
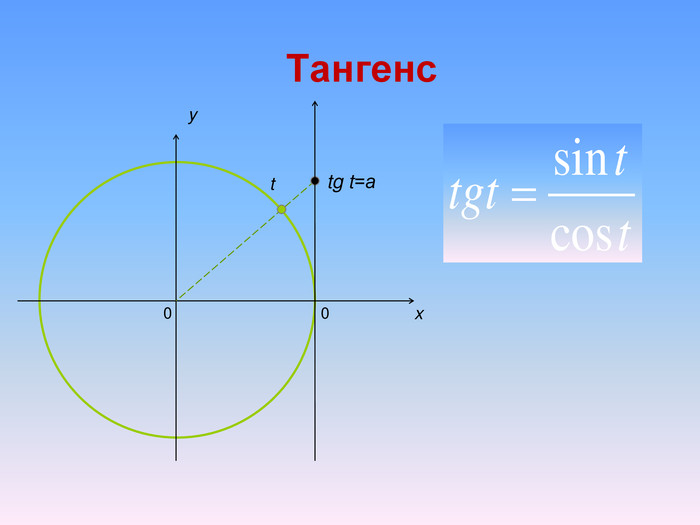
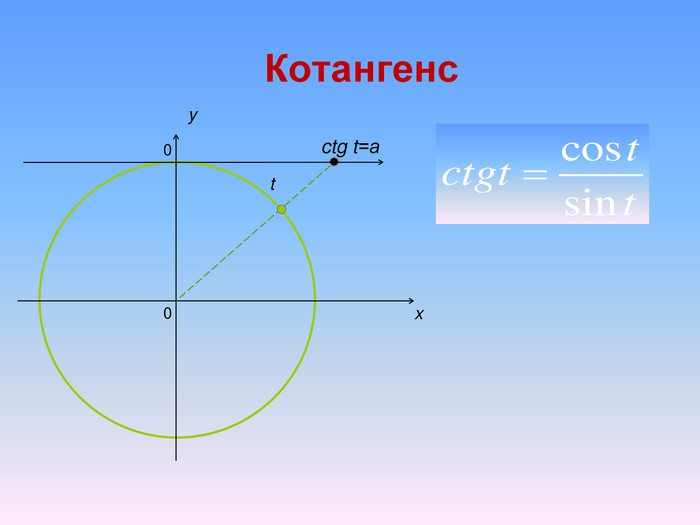
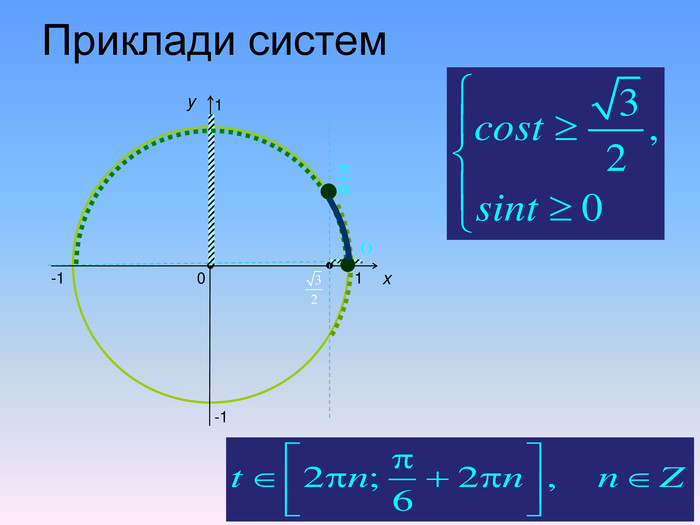
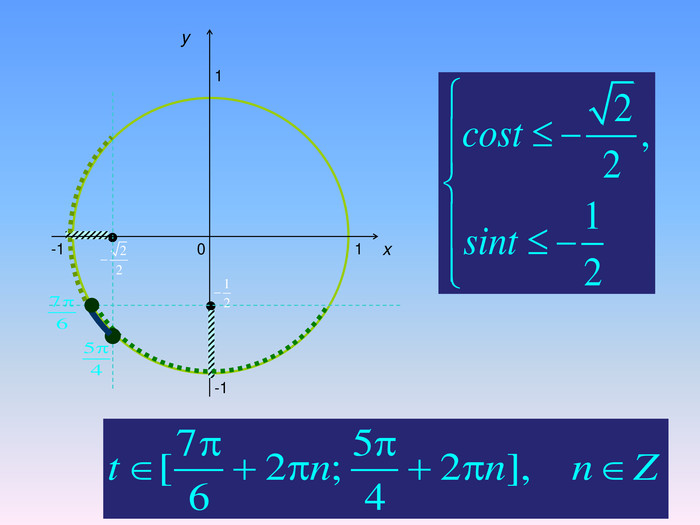
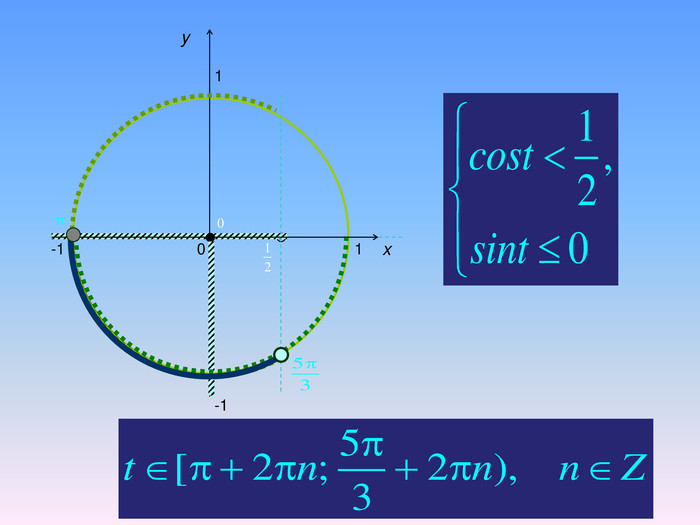
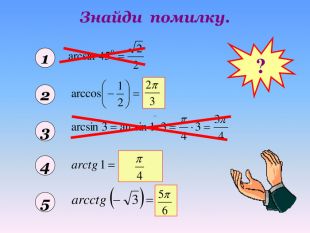
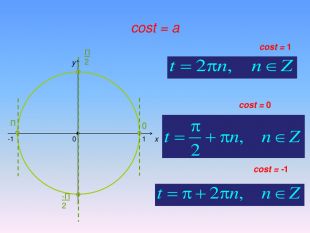
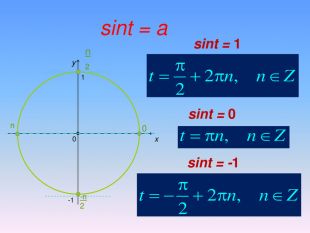
Бліц-опитування1. При якому значенні а тригонометричні рівняння sinx=a i cosx=a мають розв’язки?2. За якою формулою знаходимо розв’язок тригонометричного рівняння cosx=a при │а│ ≤ 1.3. Чому дорівнює розв’язок рівняння cosx=0? 4. Чому дорівнює розв’язок рівняння cosx=1? 5. Чому дорівнює розв’язок рівняння cosx=-1? 6. Чому дорівнює arccos(-a)?

Бліц-опитування7. За якою формулою знаходимо розв’язок тригонометричного рівняння sinx=a при │а│ ≤ 1.8. Чому дорівнює розв’язок рівняння sinx=0? 9. Чому дорівнює розв’язок рівняння sinx=1? 10. Чому дорівнює розв’язок рівняння sinx=-1? 11. Чому дорівнює arcsin(-a)?

Бліц-опитування12. За якою формулою знаходимо розв’язок рівняння tgx=a? 13. За якою формулою знаходимо розв’язок рівняння ctgx=a? 15. Чому дорівнює arcctg(-a)? 14. Чому дорівнює arctg(-a)?

Знайди помилку.12345?

Повторення. Розв’язання рівняння cost = a,sint = a за допомогою кола.

Рівняння cos t = a.0xy3. Побудувати перпендикуляр в цій точці.5. Отримані точки є рішення рівняння cost = a.at1-t1-114. Відзначити точки перетину перпендикуляра з колом. 6. Записати загальне рішення рівняння.2. Відзначити точку а на осі абсцис. 1. Перевірити умова | a | ≤ 1

cost = axycost = 0cost = -1cost = 101-1 П2-П 20 П

Рівняння sin t = a.0xyat1 П-t1-111. Перевірити умова | a | ≤ 1 2. Відзначити точку а на осі ордінат. 3. Побудувати перпендикуляр в цій точці.4. Відзначити точки перетину перпендикуляра з колом. 5. Отримані точки є рішення рівняння sin t = a.6. Записати загальне рішення рівняння.

sint = axysint = 0sint = -1sint = 101-1 П20п-п 2

Тангенс0xytg t=аt0

Котангенс0xyctg t=аt0

Яка з цих схем зайва? 123456

Які з цих схем зайві?123456

Тригонометричні нерівності Розв'язування будь-яких тригонометричних нерівностей,як правило зводимо до розв'язування найпростіших тригонометричних нерівностей:𝒔𝒊𝒏𝒙>𝒂, 𝒔𝒊𝒏𝒙<𝒂,𝒄𝒐𝒔𝒙>𝒂,𝒄𝒐𝒔𝒙<𝒂,𝒕𝒈𝒙<𝒂,𝒕𝒈𝒙>𝒂,𝒄𝒕𝒈𝒙>𝒂,𝒄𝒕𝒈𝒙<𝒂.  

Приклад1. Розв'яжіть нерівність:   sin𝒙≥𝟏𝟐 Розв'язання.І спосіб. Побудуємо графіки функцій y=sin𝒙 і 𝒚=𝟏𝟐  у. Х-11

ІІ спосіб. Розв'язування тригонометричних нерівностей за допомогою одиничного колаху. Вісь синуса співпадає з віссю ординат. Відповідь

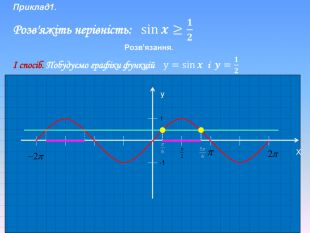
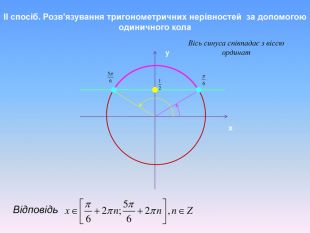
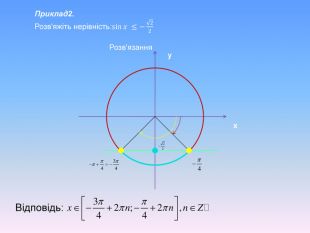
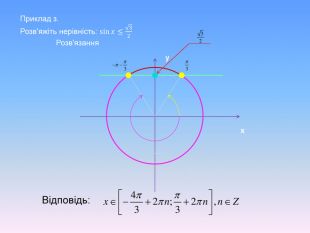
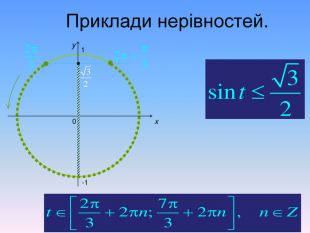
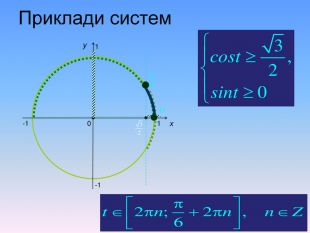
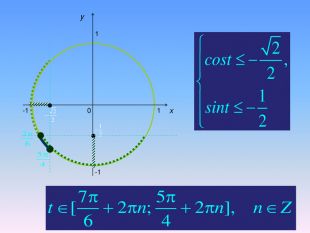
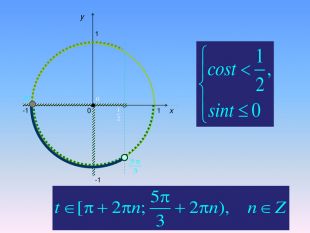
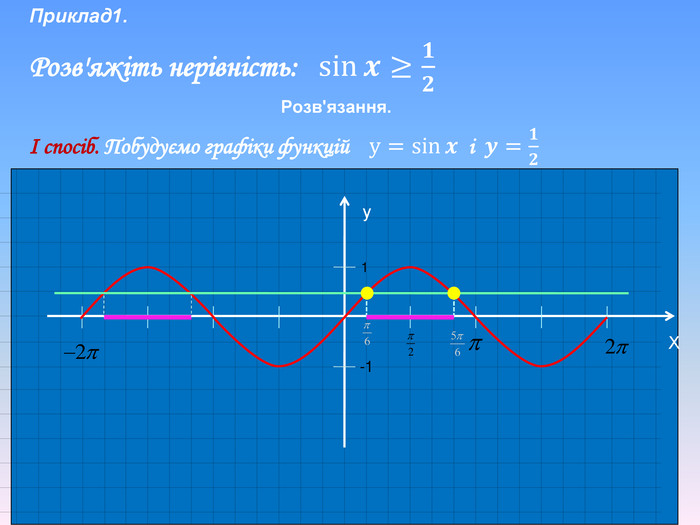
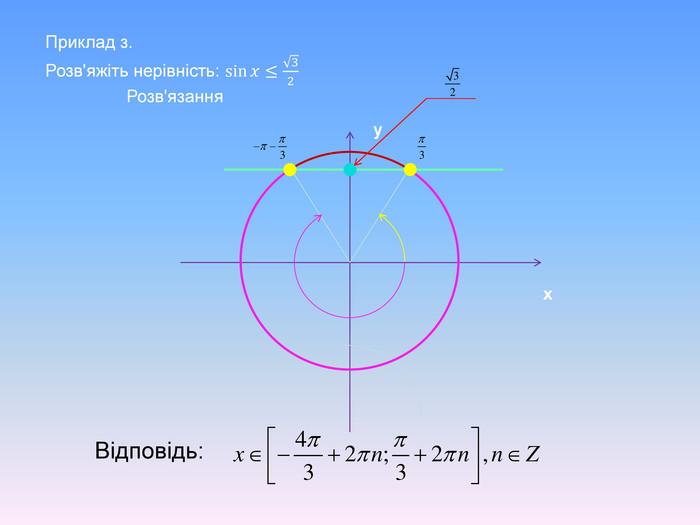
Алгоритм розв’язування нерівностей sin𝑥<𝑎,sin𝑥>𝑎 ,𝑎<1 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}1. На осі Оу (лінія синусів) позначити число а2. Провести пряму у=а3. Позначити точки перетину прямої у=а з одиничним колом 𝑃𝛼1 і 𝑃𝛼24. 𝑃𝛼1 - початок дуги, 𝑃𝛼2- кінець дуги5. sin𝑥>𝑎  5. sin𝑥<𝑎  Вибрати дугу кола,розташовану вище від прямої у=а𝛼1=arcsin𝑎,      𝛼2=𝜋−𝛼1=π−arcsin𝑎Вибрати дугу кола,розташовану нижче від прямої у=а𝛼2=arcsin𝑎,      𝛼1=−𝜋−𝛼2=−π−arcsin𝑎 6. Оскільки  𝛼1< 𝛼2 ,тоarcsin𝑎<𝑥<𝜋−arcsin𝑎−π−arcsin𝑎<𝑥

Приклад2. Розв'яжіть нерівність:sin𝑥 ≤−22 Розв'язання  ху. Відповідь:

Приклад з. Розв'яжіть нерівність: sin𝑥≤32 Розв'язання  ху. Відповідь:

Розвۥяжіть нерівність;       cos𝑥≥12 Розв'язання cos x - абсциса точки одиничного кола,що відповідає куту х ху. Відповідь:

ху. Графічно

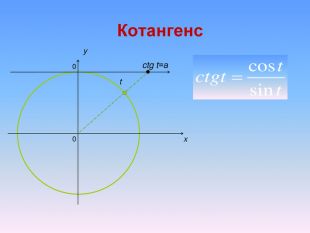
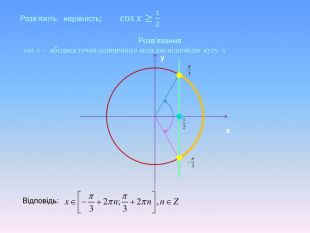
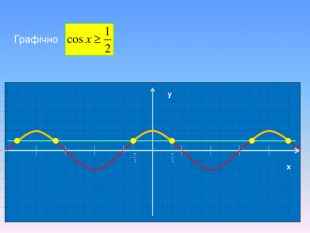
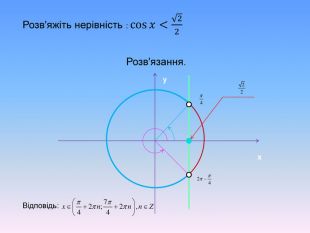
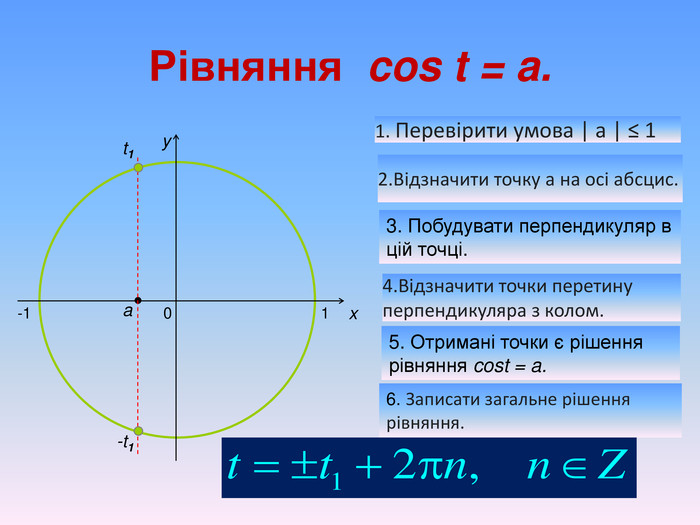
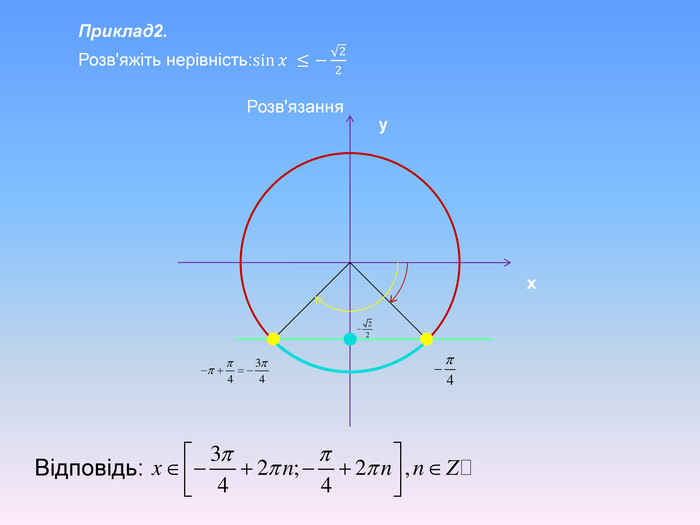
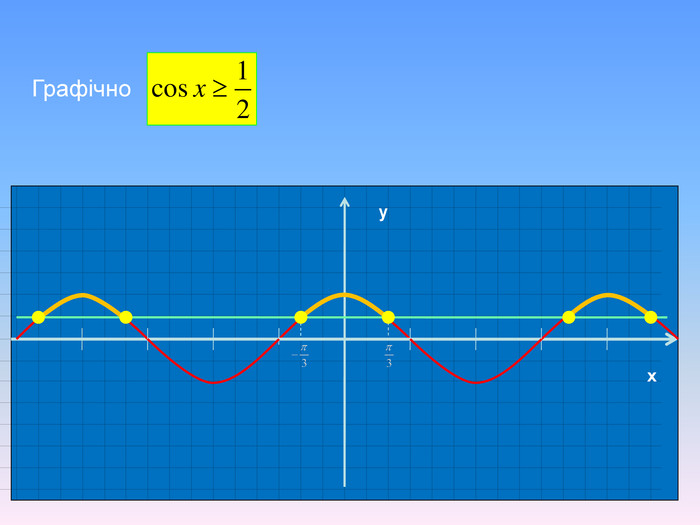
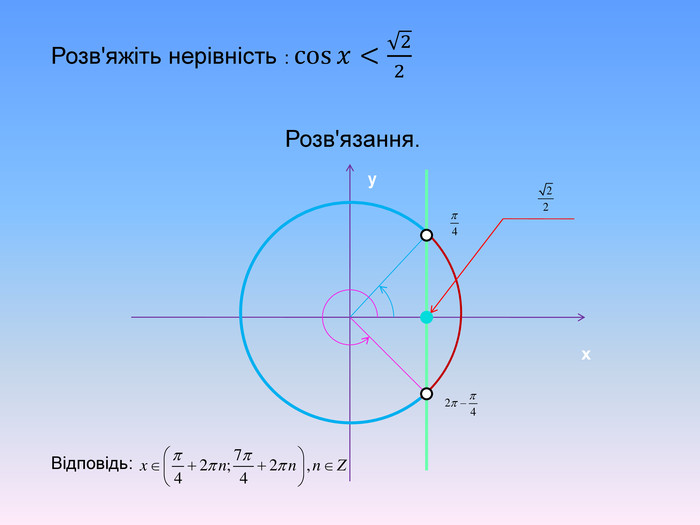
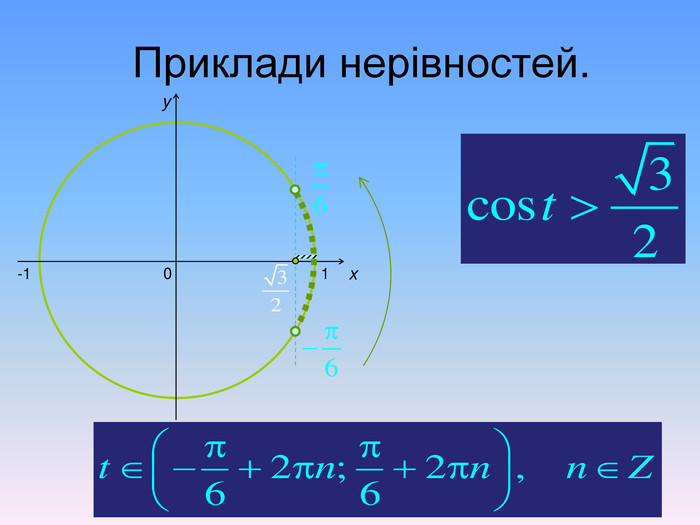
Алгоритм розв’язування нерівностей cos𝑥<𝑎,cos𝑥>𝑎 ,𝑎<1 {5 C22544 A-7 EE6-4342-B048-85 BDC9 FD1 C3 A}1. На осі Ох (лінія косинусів)позначити число а2. Провести пряму х=а 3. Позначити точки перетину прямої х=а з одиничним колом 𝑃𝛼1 і 𝑃𝛼24. 𝑃𝛼1 - початок дуги, 𝑃𝛼2- кінець дуги5.cos𝑥<𝑎, 5.    cos𝑥 >𝑎Вибрати дугу кола,розташовану праворуч від прямої х=а. Вибрати дугу кола,розташовану ліворуч від прямої х=а𝛼1=𝑎𝑟𝑐𝑐𝑜𝑠𝑎,   𝛼2=2𝜋−𝛼1=2𝜋−𝑎𝑟𝑐cos𝑎 6. Оскільки  𝛼1< 𝛼2 ,то−arccos𝑎<𝑥

Розв'яжіть нерівність : cos𝑥<22 Розв'язання. ху. Відповідь:

У загальному випадку{85 BE263 C-DBD7-4 A20-BB59-AAB30 ACAA65 A}Вид нерівностіМножина розв'язків ,

Приклади нерівностей.0xy-11

0xy-11 Приклади нерівностей.

Система нерівностей:0xyata-ta-11btbπ-tb1-11. Відзначити на окружності рішення першої нерівності. 2. Відзначити рішення другого нерівності. 3. Виділити спільне рішення (перетин дуг). 3. Віділіті СПІЛЬНЕ решение (перетин дуг).

Приклади систем0xy-111-1

0xy11-1-1

0xy11-1-1

Домашне завдання. П.4, § 30, № 30.2(1-7), №30.5 (1), 30.7 (1).

Дякую за працю.