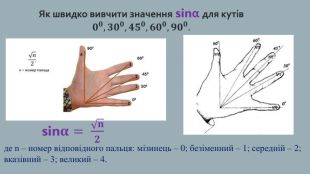
Тригонометричні рівняння

















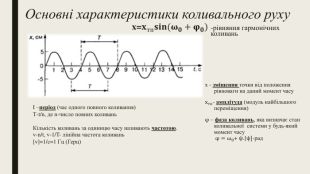
![x=𝐱тп𝐬𝐢𝐧(𝛚𝟎+𝛗𝟎) Основні характеристики коливального руху-рівняння гармонічних коливаньx - зміщення точки від положення рівноваги на даний момент часуxтп- амплітуда (модуль найбільшого переміщення) φ – фаза коливань, яка визначає стан коливальної системи у будь-який момент часу φ=ω0+ ψ.[ψ]-рад I –період (час одного повного коливання)Т-t/n, де n-число повних коливань. Кількість коливань за одиницю часу називають частотою.v-n/t, v-1/T- лінійна частота коливань[v]=1/с=1 Гц (Герц) x=𝐱тп𝐬𝐢𝐧(𝛚𝟎+𝛗𝟎) Основні характеристики коливального руху-рівняння гармонічних коливаньx - зміщення точки від положення рівноваги на даний момент часуxтп- амплітуда (модуль найбільшого переміщення) φ – фаза коливань, яка визначає стан коливальної системи у будь-який момент часу φ=ω0+ ψ.[ψ]-рад I –період (час одного повного коливання)Т-t/n, де n-число повних коливань. Кількість коливань за одиницю часу називають частотою.v-n/t, v-1/T- лінійна частота коливань[v]=1/с=1 Гц (Герц)](/uploads/files/174717/415311/471321_images/18.jpg)














Встановіть відповідність «Рівняння - корені» {69 CF1 AB2-1976-4502-BF36-3 FF5 EA218861}1sinx=1 2x=(−1)nπ6+ πk, k∈Zс2cosx=−22x=±3π4+ 2πk, k∈Zі3sinx=0x= πk, k∈Zм4cosx=0x=π2+ πk, k∈Zя 5sinx=1x=π2+ 2πk, k∈Zт6cosx=1x= 2πk, k∈Zа 7tg x=−1x=− π4+ πk, k∈Zш8sinx=−1x=− π2+ 2πk, k∈Zл9cosx=−1x=π+ 2πk, k∈Zю10sinx=−22x=(−1)n+1π4+ πk, k∈Zб{69 CF1 AB2-1976-4502-BF36-3 FF5 EA218861}1с2і3м4я 5т6а 7ш8л9ю10б
Сучасний зміст і вид тригонометрії- це заслуга Леонарда Ейлера. Його трактат «Введення в аналіз нескінчених» (1748) містить визначення терміна «тригонометричні функції», яке еквівалентне сучасному. Визначення тригонометричних функцій на всій числовій прямій стало можливим завдяки дослідженням Ейлера не тільки допустимих негативних кутів, але і кутів більших за 3600. Саме він в своїх роботах вперше довів, що косинус і тангенс прямого кута негативні. Розкладання цілих ступенів косинуса і синуса теж стало заслугою цього вченого.
Синус – латинський переклад арабського слова «джайб» - пазуха, виріз сукні. Це слово походить від індійського «джива» - тятива лука, хорда. Саме так називали синус в давньоіндійських математичних трактатах. Сучасне позначення sin вживали: Томас Сімпсону 1737-1750 роках. Леонард Ейлеру 1748-1753 роках. Д’Аламбер у 1754 році Жозеф Лагранж у 1774 році
Тангенс – у перекладі з латинської «дотичний». Тангенс, як тінь вертикальної жердини, був введений арабським математиком Абу-ль-Вафой у Х ст. – цей термін належить Е. Гюнтеру. В арабській математиці котангенс винайшов Ал-Баттані (ІХ ст.). Графік котангенса для першої чверті побудував Грегорі у 1668 році. Котангенс. Ал-Баттані, арабський астроном та математик. Джеймс Грегорі, шотландський математик та астроном
Цікавими є той факт, що поняття «тангенса» і «котангенса», як і перші таблиці цих величин, з’явились не внаслідок розгляду тригонометричного кола, а із вчення про сонячний годинник. У давнину час вивчали за сонячним годинником. Вивчаючи залежність довжини тіні будівлі від кута нахилу сонячних променів, математики винайшли дві нові тригонометричні функції.
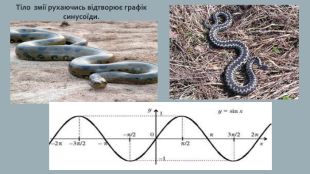
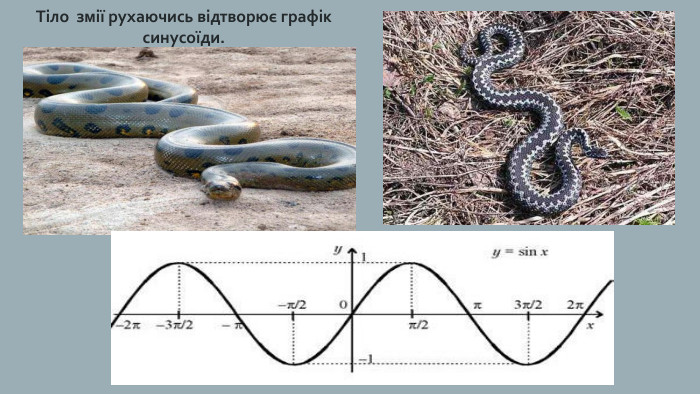
Хвилі на морі мають форму, що нагадує синусоїду. І це не випадково, бо багато фізичних величин періодично змінюються і можуть бути описані за допомогою тригонометричних функцій. Коливання– найпоширеніша форма руху в навколишньому світі та техніці. Коливаються дерева, хвилі під дією вітру, поршні у двигуні автомобіля тощо.
x=𝐱тп𝐬𝐢𝐧(𝛚𝟎+𝛗𝟎) Основні характеристики коливального руху-рівняння гармонічних коливаньx - зміщення точки від положення рівноваги на даний момент часуxтп- амплітуда (модуль найбільшого переміщення) φ – фаза коливань, яка визначає стан коливальної системи у будь-який момент часу φ=ω0+ ψ.[ψ]-рад I –період (час одного повного коливання)Т-t/n, де n-число повних коливань. Кількість коливань за одиницю часу називають частотою.v-n/t, v-1/T- лінійна частота коливань[v]=1/с=1 Гц (Герц)
𝒔𝒊𝒏𝜶𝒔𝒊𝒏𝜷=𝒏𝟏𝒏𝟐де n1=1, n2≈1,33 − відповідно показники заломлення повітря і води, α−кут падіння, β−кут заломлення світла. Сила, що діє на рухому в магнітному полі заряджену частинку називають силою Лоренца. Вона пропорційна заряду частинки векторному добутку поля і швидкості руху частинки. F=qv. Bsin𝜶 - сила Лоренца, де q-заряд; v-швидкість заряду; В-магнітна індукція; 𝛼−кут між векторами 𝑣 та 𝐵
Яким би складним не було тригонометричне рівняння, розв’язати ми його зможемо за умови дотримання певних орієнтирів (рекомендацій). Звести тригонометричні функції до одного аргументу. Звести тригонометричне рівняння до однієї функції. В інших випадках переносимо всі члени рівняння в ліву частину і намагаємось розкласти на множники.


про публікацію авторської розробки
Додати розробку