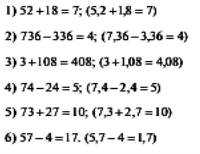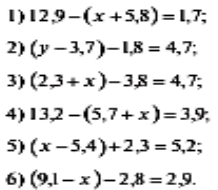Творча робота "Дидактичні ігри на уроках математики"

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Дидактичні ігри на уроках математики

 

Потрібно сьогодні сказати лише те, що доречне сьогодні,

все інше відкладемо і скажемо, коли буде потрібно.. 

                                                                                         Горацій

 

     Учитель відбувся тоді, коли він хоче йти на роботу і, незважаючи на альтернативу, не змінює професію, коли він бачить у дітях, яких навчає і виховує, результат. Кожен учитель має нести відповідальність за те, якими учні вийшли з його уроку. Тобто після уроку в дітей не повинна згаснути жага до знань і любов до життя. На уроці учень має здобувати знання і вчитися ними оперувати, витрачаючи на це лише частку своїх сил.

 

     Життя – одне і ці 45 хвилин більше ніколи не повторяться. Якщо дитина протягом уроку працювала – вчилася пояснювати, аргументовано відтворювати засвоєне, публічно захищати свою думку, і при цьому не втратила віри в себе, то урок не пройшов для неї даремно. Відомо, що діти йдуть до школи за спілкуванням з друзями, з учителем. Найбільшу радість і задоволення вони отримують від роботи на уроці, що дозволяє відкрити себе і свої задатки, здібності тощо. Очі дітей загоряються у той момент, коли їх навчають чомусь значному, важливому в житті, а не для отримання оцінок.

 

     Розкрити особистість учня можливо, якщо учитель йтиме на урок не тільки зі знанням навчального матеріалу, методів і прийомів навчання, набором красивих задач і вмінням їх майстерно розв'язувати, а й із різноманітними і цікавими способами і прийомами організації праці учнів. Процес навчання потребує напруженої розумової роботи дитини і її власної активної участі в цьому процесі. Пояснення і демонстрація, самі по собі, ніколи не дадуть справжніх, стійких знань. Цього можливо досягти тільки за допомогою інтерактивного навчання. Умовна класифікація технологій інтерактивного навчання наступна:

• інтерактивні технології кооперативного навчання;
• інтерактивні технології колективно-групового навчання;
• ситуативне моделювання;
• опрацювання дискусійних питань.

 

Саме до технологій ситуативного моделювання відносять гру. Навчально-ігрове спілкування несе на собі велике навантаження, оскільки виконує наступні функції:

• виховну – розкривається почуття колективізму, сміливості, рішучості, виховуються морально-етичні якості;
• пізнавальну – розвиток пізнавальної активності, збагачення знань новою інформацією;
• гедонічну – проживаються раніше невідомі відчуття, формується оптимальний життєрадісний настрій;
• компенсаторну – через гру знімається психогенне і фізичне напруження, підвищується загальний тонус, з’являється почуття розкутості.

1

Тому ділові та імітаційні ігри знаходять широке застосування у найрізноманітніших сферах діяльності: економіці, політиці, екології, міському плануванні, освіті.

     Кожний учитель прагне зацікавити учнів предметом, який він викладає, бо це є запорукою успішного навчання.

     На своїх уроках для виховання в учнів інтересу до навчання практикую складання і розгадування кросвордів. Особливо люблять діти їх розгадувати, якщо потрібно дізнатись цікаве ключове слово. Наприклад, автора крилатого вислову «Математику вже тому вчити треба, що вона розум до порядку приводить» ви дізнаєтесь, якщо розгадаєте кросворд.

 

1. Геометричне тіло.
2. Твердження, що приймається без доведення.
3. Її використовують для наочного зображення різних величин.
4. Множина точок площини, рівновіддалених від однієї точки площини.
5. Наука про одержання, зберігання, передавання і перетворення інформації.
6. Компонент дії додавання.
7. Відрізок, що сполучає центр кола з точкою кола.
8. Частина круга між двома радіусами.
9. Рівність зі змінною.

 

				1
		2
3
			4
	5
					6
	7
		8
				9

   

 

     На уроках узагальнення і систематизації за допомогою «Угорського  кросворду»  перевіряється знання теоретичного матеріалу. Кожна буква у сітці кросворду використовується тільки один раз. Слова читаються під прямим кутом.

     До кожного поняття в дужках вказано кількість букв у слові.

     Щоб зацікавити учнів 7 класу при ознайомленні з новим предметом – геометрією, після вивчення теми «Найпростіші геометричні фігури та їх властивості» пропоную розгадати такий кросворд:                                                                                               2

1. Наука про властивості геометричних фігур. (9)
2. Як називається частина прямої, яка складається з усіх точок цієї прямої, що лежать між двома даними точками? (8)
3. Основні геометричні фігури на площині. (5; 5)
4. Частина прямої, що складається з усіх її точок. (7)
5. Півпрямі, що утворюють кут. (7)
6. Частина площини, обмежена двома променями, що виходять з однієї точки. (3)
7. Частина площини, що утворюється в результаті розбиття її прямою. (10)

 

 

Р	П	Т	У	К	А
О	С	Т	О	Ч	К
М	І	О	Т	И	Г
Ь	Н	Р	О	Н	Е
Я	Р	П	Е	М	О
М	А	Р	Т	В	І
І	П	І	Я	Р	Д
В	К	О	З	І	А
П	Л	О	Щ	И	Н

    

 

     Для учнів 6 кл., після вивчення теми «Координатна пряма. Модуль числа», можна запропонувати розгадати такий кросворд:

1. Пряма, на якій взято початок відліку, одиничний відрізок, вказано напрям. (11)
2. Числа, що лежать зліва від нуля. (7)
3. Числа, що лежать справа від нуля. (7)
4. Число, що показує положення точки на прямій. (10)
5. Числа, що рівновіддалені від початку відліку і лежать по різні боки від нього. (10)
6. Відстань від початку відліку до точки, що зображує число. (6)
7. Що зображує початок відліку на координатній прямій? (6)

 

К	О	А	К	Ч	І	Н	І
А	О	Р	Д	О	Т	Т	Н
Т	А	Н	И	О	Д	А	М
Т	О	Р	П	Д	М	О	Є
И	Ж	Н	І	Т	Н	Д	Д'
Л	Е	Р	Д	А	А	У	І
К	О	О	И	Н	Ь	Л	В

     

     Для сильних учнів можна проводити конкурс художників: три учні працюють біля дошки, клас працює самостійно. Дітям ця гра дуже подобається.

 

 «Птаха»: (-9; 7), (-7; 8), (-6; 10), (-3; 10), (-1; 7), (8; 1), (15; -2), (13; -4),

 (6; 0), (4; -1), (3; -1), (1; -7), (-1; -7), (1; -6), (2; -1), (0; -1), (-2; -7), (-4; -7),

(-2; -6), (-1; -1), (-5; 2), (-6; 5), (-7; 6), (-9; 7)                                                                     3

«Квітка»: (-1;7), (-2; 7), (-3; 8), (-3; 8), (-3; 12), (-4; 13), (-3; 4), ( -2; 13),

 (-1; 14), (0; 13), (1;14), (2; 13), (3; 13), (4; 13), (3; 13), (3; 8), (2; 7), (-1; 7),

 (-1; -3), (-5; 1), (-8; 1), (-10; -1), (-10; -3), (-8; -1), (-5;-1), (-1; -5), (-1; -14),

 (1; 14), (1; -5), (5; -1), (8; -1), (10; -3), (10; -1), (8; 1), (5; 1), (1; -3), (1; 7).

 

     Можна запропонувати обернене завдання: намалювати будь – який малюнок, що має конфігурацію ламаної, і записати координати її вершин.

     При проведенні дидактичної гри на уроці часто використовую принцип змагання між групами учнів. Кожний учитель не задоволений, якщо бачить на своїх уроках сумні обличчя. Коли ж учні працюють захоплено, то й учитель відчуває задоволення. Уникнути пасивності учнів на уроці допомагають командні математичні змагання. Змагання надають грі емоційного характеру. Учні не тільки самі прагнуть добре виконати завдання, але й спонукають до цього своїх товаришів, допомагаючи їм.

     Інколи, як домашнє завдання, на вихідні чи на канікули пропоную написати казку чи фантастичний твір. Такі завдання формують уяву, а це особливо важливо для учнів 5-7 класів для опанування геометричного матеріалу.

     До перевірки таких задач, творчих завдань корисно залучати всіх учнів класу, організовуючи взаємне рецензування, колективне обговорення цих завдань та їх оцінювання.

 

Зашифровані завдання.  Знайти корені рівнянь і вибрати відповідну пару з літерою. Якщо рівняння будуть розв’язані правильно, то учні отримають ключове слово. Наприклад:

1.  x² + 5x – 6 = 0.      (-6; 1)

1. y² + 10y – 24 = 0.  (-12; 2)
2. y² – 4у – 5 = 0.      (5;  -1)
3. x² – 5x – 14 = 0     (-7; 2)
4. x² – 8x + 15 = 0     (3; 5)
5. y² – 8y + 12 = 0     (2; -6)

 

Картки – відповіді: У (5; -1), С (6; -1), Д (-6; 1), Ж (-7; 2), Я (4; 3),Т (12; -2),

Р (-12; 2), Л (-5; -3), А (2; 6), Б (5; 3)

 

Відповідь: Ключове слово “Дружба”.

 

     При вивченні теми “Додавання і віднімання раціональних чисел” дуже корисною є дидактична гра “Фішка”.

     Мета її проведення – виявлення навичок додавання і віднімання цілих чисел, а також їх порівняння. Спочатку фішка стоїть на одній з клітинок лінії старту. Учень рухає фішку по таблиці з числами. За один хід за правилами гри він може її пересунути на сусіднє поле по вертикалі чи діагоналі. При переході з однієї клітинки на другу потрібно додавати число, записане в клітинці, на яку поставили фішку. Виграє той, хто на лінії фінішу одержить найбільше число.

     В ході гри школярі, крім обчислень, вчаться вибирати найбільше серед від'ємних і додатних чисел.

 

 

4

• Фініш

9	8	7	6	5	4	3	2	3	4	5	6
-10	-9	-8	-7	-10	-9	-8	-7	-10	-9	-8	-7
47	45	50	42	39	37	50	35	52	40	38	35
-7	-6	-4	-5	-6	-9	-7	-8	-9	-7	-8	-9
23	24	25	26	24	28	29	30	22	31	32	33
100	100	100	100	100	100	100	100	100	100	100	100

• Старт

 Математична казка

Хочете казку?

Відгадайте загадку “Знайдіть усно корінь рівняння n + 12705 : 121 = 105”.

Клас поділити на три команди.

В деякому царстві, в деякому государстві жив-був Іван – Царевич. Було в нього три сестри: Анастасія, Ольга, Ярославна. Батьки в них померли. Віддав царевич сестер своїх заміж за царів мідного, срібного, золотого царства. Рік прожив він без сестер і стало йому сумно. Ось і відправився Царевич–брат в путь. По дорозі зустрів Марічку. Закохався. Але зла Баба Яга викрала Марічку. Царевич з вірними воїнами поїхав рятувати свою наречену. Дісталися вони ріки, а там величезний камінь перекрив дорогу на міст, на якому три рівняння (з номерами команд):

(y – 371) + 546 = 277  (1)

(127 + m) – 98 = 32  (2)

(x + 379) – 197 = 183  (3).

Якщо їх вірно розв’язати, то камінь відкриє дорогу.

Довго їхали по лісу воїни, поки дорога не довела їх до хатинки Баби Яги. Але щоб двері хатинки відчинилися, треба відкрити три замки.

65 +2x = 59,                         24 – 3x = 21,                         75 – 5x – 15  = 30,

y(58 – 27) = 62.  (1)             (25 + 8)n = 99.  (2)                92 – 3c = 392 – 311  (3)

Прощаючись з Іваном – Царевичем, кіт Баби Яги розповів йому про силу коренів рівнянь. Коли треба відчинити або закрити замок, треба назвати корені рівнянь. Чорний ворон підслухав та розповів Бабі Язі. Злодійка схватила Царевича, воїнів та кинула в глибоке підземелля, замкнувши на шість замків.

35: y – 20 = 15,                        m : 2 + 35 = 36,                     x : 12 ^. 2 = 72,

(5 – d ) ^. 3 = 4d – 3 ^. 2  (1)        (3 + x) ^. 5 = 3x + 57  (2)        (7 + y) ^. 5 = 7 ^. 5 + 3 ^. 5  (3)

Царевич назвав корені всіх рівнянь. Двері підземелля відчинилися. Звільнили воїни Марічку, згуляли весілля та стали  жити – поживати, добра наживати.

 

     Дидактичні ігри на уроках математики мають важливе значення. Урок стає цікавим, діти менше втомлюються, а між тим виконують потрібний об’єм роботи, зберігаючи високу трудову активність упродовж усього уроку.                                                        5

      В гру включаються і діти, які на звичайному уроці працюють не дуже активно. Дидактичні ігри на уроці навчають і виховують, допомагають здобувати нові знання і застосовувати на практиці вже засвоєні. Дуже важливе значення на уроках математики мають усні вправи.

 Магічні квадрати

 

     Алгоритм складання магічних квадратів третього порядку:

• у першу стрічку чи стовпчик магічного квадрата записати три довільних числа (вирази);
• знайти магічну суму S;
• знайти 1/3 S. Це число (вираз) записати на перетині діагоналей “магічного” квадрата;
• знайти і записати решту чисел (виразів) магічного квадрата.

0	1	2		а2	3в2	- 4а2
3	1	- 1		в2 – 6а2	в2 – а2	в2 + 4а2
0	1	2		2в2 + 2а2	- в2 – 2а2	2в2 – 3а2

Складемо «магічний» квадрат 4Х4:

• Візьмемо 16 послідовних членів арифметичної прогресії:

     а; а + d; а + 2d; …. a + 15d. Їх сума дорівнює   S₁₆ = 16а + 120d.

• Якщо позначити суми в стрічках через S_1, S_2, S_3, S_4, в стовпцях – S_5, S_6, S_7, S₈, по діагоналям – S₉ і S₁₀, то за умовою S₁  = S₂  = S₃  =…= S₉ = S₁₀.
• Сума чисел у стовпчику, стрічці, або по діагоналі дорівнює

     (16а + 120d): 4 = 4а + 30d.

• На кінцях діагоналей треба, щоб були числа а і а+15d, або а + 10d і а + 5d. Другими числами першої діагоналі можуть бути числа а + 6d і а + 9d,   другої  –  а + 12d і а + 3d, тому що сума по діагоналі дорівнює 4а + 30d.

 

А	А + 11d	a + 14d	a + 5d
a + 13d	A + 6d	a + 3d	a + 8d
a + 7d	A + 12d	a + 9d	a + 2d
a + 10d	A + d	a + 4d	a + 15d

6

Індивідуальне лото

 

    Учень розв’язує завдання на карточці. Якщо відповідь правильна, то після того, як покрити велику карту малими картками, вийде шифр: малюнок, слово, фігура.

Велика карта

 

7	24	36
2	22,4	12

 

Карточки

 

34,47 . 0,9 + 5,53 . 0,9			0,8 . 5,6 . 5				28,53 . 0,8 + 1,47 . 0,8
4 . 1,75				0,5 . 3,4 : 2				7,86x + 2,14x, якщо x = 0,02
	7,86x – 2,86x, якщо x = 0,4				13,56x + 6,44x, якщо x = 0,6

 

 

7

Розробки уроків

 з елементами дидактичних ігор

 

 

«ЛОГІЧНИЙ ОЛІМП»

РОЗВ'ЯЗУВАННЯ ЦІКАВИХ ЛОГІЧНИХ ЗАДАЧ

Мета уроку: формувати в учнів навички розв'язування логічних задач, навички взаємоконтролю і самоорганізації; розвивати ло­гічне мислення; відповідальність, колективізм, волю до перемоги.

Люди помиляються саме тому, що їм бракує логіки.

                                                                                                                        Г. В.Лейбніц

ХІД УРОКУ

I. Оголошення теми, мети і завдань

II. Ознайомлення з планом уроку, з правилами роботи на занятті

Клас розподілено на дві команди. Завдання учням пропонує вчитель. По одному учню від кожної команди одночасно розв'язують завдання. Оцінювати від­повіді учнів, враховуючи швид­кість виконання, правильність, культуру записів.

І етап гри. Бліц-опитування

По одному учню від кожної ко­манди виходять до дошки й отримують картку із завданнями. Учні записують на дошці завдання і відповідь. У разі помилки ко­манда може допомогти.

Завдання для команд
І команда	II команда
Вставити пропущені числа та слова
1, 1, 3, 3, 7, ?,  4, 4, ?, 9; циркуль(5;6;7) цирк; стимул (1; 2; 3)?	3, 3, 3, 7, 7, 7, 2, ?,  2, 6, 7, 6; тріска (1; 4; 5) ріка; правило (5; 6)?

 

II етап гри

До дошки виходять «спеціалісти» швидкого мислення. Необхідно відповідати на запитання, роз­мірковуючи над кожним не біль­ше ніж ЗО секунд.

8

Завдання для команд

І команда

1.  Семеро чекали на восьмого 14 хв. Скільки хвилин чекав кожний окремо?

2.   Як називається другий місяць літа?

3.   Петро ліг спати о 9 годині вечо­ра, а будильник поставив на де­сяту  годину ранку.   Скільки часу він проспав?

4.   Яке каміння в морі?

5. Стіл має чотири кути. Один кут спиляли. Скільки кутів залишилося?

6.   Скільки   пар   ніг   у   коня? А в курки?

II команд

1. Вісім яєць варилося 4 хв Скільки  хвилин   варилося   кожне яйце?              

2.  Що таке 33 січня?

3. О 2 годині дня у Львові падав дощ. Чи буде сонячна погода у Львові через 10 годин?

4. У двох носорогів два роги. Скільки рогів у двадцяти носо­рогів?

5.   Скільки кінців має одна пали­ця? А дві?

6.   Яких каменів немає в річці?

III етап гри

Кожна з команд одержує по дві задачі, колективно розв'язує їх.

І команда

1.   Коли батькові було 27 років, то синові було лише 3 роки, а зараз синові у три рази менше років, ніж батькові. Скільки років кожному з них?

2.   Хазяїну треба перевезти козу, капусту та  вовка  на  інший берег. Як це зробити, якщо в човні може вміститися тільки хазяїн, а з ним тільки вовк, або тільки коза, або тільки капуста? Якщо залишити вовка з козою, то вовк з'їсть козу, а якщо залишити козу з капустою, то коза з'їсть капусту. То як бути?

II команда

1.               Дочці зараз 10 років, а матері 36. Через скільки років мати буде удвічі старша за дочку?

9

2.   Десятьом дорослим чоловікам треба переправитися через річку. Та міст зламаний, а річка глибока. Як бути? Раптом вони помітили двох хлопчиків на човні. Проте човен був таким малим, що міг витримати тільки одного чоло­віка або двох хлопчиків — не більше. Але всі благополучно перепра­вилися на другий берег. Як?

IV етап гри

 

Завдання для команд «Хто швидше»

Сформулювати правило, за яким записані числа в першому квад­раті, і за тим самим правилом за­повнити два наступні квадрати.

1	3	3		0	5	?		4	1	?
2	4	8		1	3	?		3	1	?
2	12	24		?	?	?		?	?	?

 

Перемагає команда, яка швидше впоралася із завданням та набра­ла більшу кількість балів. Вона досягла вершини «Логічного Олімпу».

III. Підбиття підсумків гри. Виставлення оцінок

 

 

10

            

 

ПОДОРОЖ ДО СЕМИ ЧУДЕС СВІТУ

 

Інтегрований урок з алгебри і світової культури

у 7 класі

 

 

ТЕМА УРОКУ.   Розв’язування систем лінійних рівнянь з двома змінними.

ТИП УРОКУ.    Урок узагальнення і систематизації знань.

МЕТА УРОКУ.

Дидактична: узагальнити і систематизувати знання з даної теми; повторити способи (графічний, додавання, підстановки) розв’язування систем; закріпити вміння і навички застосовувати теоретичний матеріал до розв’язування  систем лінійних рівнянь з двома змінними.

Розвиваюча:   розвивати логічне мислення, вміння вибирати раціональний спосіб розв’язування; розвиток міжпредметних зв’язків (математика, історія, культура).

Виховна: естетичне виховання учнів; виховання пізнавального інтересу до математики.

ХІД УРОКУ

1. МОТИВАЦІЯ НАВЧАЛЬНОЇ ДІЯЛЬНОСТІ

Якщо хочеш досягнути

У житті своїх вершин –

Математику збагнути

Маєш тонко до глибин.

 

    Вчитель культури. Мандрівка до 7 чудес світу – це подорож не лише в далекі країни, але і в далеке минуле. До тих творінь людського генія, які своєю художньою і технічною майстерністю дивували і дивують світ.

     Однією з таких країн є Єгипет – країна давньої культури. В той час, коли предки європейських народів мешкали в печерах, Єгипет був країною з палацами і храмами, з розвиненою астрономією, медициною, гарними ювелірними прикрасами.

 

     Вчитель математики. Саме тут було відоме твердження про властивості прямокутного трикутника, яке узагальнив і довів древнегрецький математик Піфагор.

     У 8 класі на уроках геометрії ми будемо вивчати тему “Теорема Піфагора”.               

                                   Теорема Піфагора – універсальна,

                                    Її застосування – багатогранне.

Теорему Піфагора використовують всюди –

В науці, мистецтві, архітектурі.

У часи найдавніші і в нашій вже ері

Творцям була відома прекрасна теорема.

А ще творцям – математикам відома система.

Її розв’язування – багатогранне

І хто першим систему розв’яже,

Той дорогу до чуда укаже.

3x – y  = 11,

5x + 6y  = 26.  

                                      (4; -1),     (3; -2),     (4; 1),     (-4; -1),     (-3; 2)

                                                                    Піраміда                                                       11

2.  АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ

Вчитель культури.

 

Піраміда Хеопса

Є найдавнішою з 7 чудес світу і єдиною, що збереглася до наших днів. Висота піраміди досягає 147м, а площа основи – 55000 м². Єгиптяни вірили, що сходинками піраміди фараони піднімалися в небо.

 

Вчитель математики.

 

     І ми з вами, сходинка за сходинкою, повторимо теоретичний матеріал вивченої теми:

• Закінчити речення: “Системою рівнянь називається…”                                            (два або декілька рівнянь, у яких потрібно знайти всі спільні розв’язки).
• Що є розв’язком системи  лінійних рівнянь з двома змінними?

(розв'язком системи  рівнянь є пара чисел)

• Запишіть загальний вигляд системи лінійних рівнянь з двома змінними.

                                                                                   а₁x + в₁y  = с₁,                                                  

                                                                                   а₂x + в₂y  = с₂.

• За якої умови система має єдиний розв’язок?

(а₁:а₂ = в₁:в₂ = с₁:с₂)  

• За якої умови система не має розв’язків?

(а₁:а₂ = в₁:в₂ = с₁:с₂)

• За якої умови система має безліч розв’язків?

(а₁:а₂ = в₁:в₂ = с₁:с₂)

• Які вам відомі способи розв’язування систем лінійних рівнянь з двома змінними?       (графічний, додавання, підстановки).

 

 Вчитель культури. Ми залишаємо перше чудо - Єгипетські піраміди. Одне з чудес, що найкраще збережене часом. Недарма кажуть: “Усе на світі боїться часу, але час боїться пірамід”. Збудовані для уславлення царів, вони самі стали славою Єгипту.   Вирушаємо далі.

 

3. УЗАГАЛЬНЕННЯ ТА СИСТЕМАТИЗАЦІЯ ЗНАНЬ

 

Вчитель культури.

 

Храм Зевса в Олімпії

У самому серці Греції, на священній Олімпійській землі архітектором Лібоном був зведений храм. На честь верховного бога Зевса. Скульптор Фідій створив статую Зевса, що вражає своєю величністю. Одяг Зевса виготовлено із чистого золота, трон – з кедрового дерева. Здається, що Зевс встає з трону, настільки майстерно виготовлена споруда. Найсильнішому богові – Зевсові в Олімпії присвячувались спортивні змагання.

 

Храм Артеміди в Ефесі

Донькою бога Зевса була Артеміда, саме на її честь в Ефесі був зведений храм із чистого мармуру.                                                                                                  12

Складається храм із 120 колон висотою 20м. У головній залі стоїть статуя заввишки 15м, оздоблена дорогоцінним камінням – статуя Артеміди – богині мисливства.                                                                                                                        

Будували храм 120 років, а спалили – за 1 день. Як це вдалося підпалювачу Герострату, не знають і досі. Адже храм було збудовано з суцільного мармуру. Давньогрецька богиня Артеміда була сестрою бога Аполлона і дуже полюбляла загадки.

Вчитель математики.

Загадка Артеміди

 

Зашифроване завдання

 

1.

Які з пар чисел є розв’язком системи рівнянь?

2x + y = 5,

3x + 4y = 15     (2; 1),  (1; 3),  (3; - 1),  (0; 5).

                            П         О          А          С

 

2.  

Які з пар чисел є розв’язком системи рівнянь?

x + 2y = 4,

4x + 5y = 7    (0; 2),  (-2; 3),  (-4; ;4),  (3; -1).

                           О          Л           Е           Х

 

3.

Які з пар чисел є розв’язком системи рівнянь?

5x + 2y = 18,

x – 3y = 7   (0; 9),  (2; 4),  (4; -1),  (6; -6).

                          М        А          О         К

 

4.

Які з пар чисел є розв’язком системи рівнянь?

2x + 2y = 4,

4x + 3y = 7     (2; -1),  (4; - 4),  (-2; 5),  (0; 2).

                           У           Я           К         Д

 

5.

Які з пар чисел є розв’язком системи рівнянь?

3x – y = 5,

5x + 2y = 12      (1; 2),  (3; 4),  (2; 1),  (5; 10).

                             О         Х         С          М

 

Вчитель культури.

 

Колос Родоський

У східній частині Середземного моря знаходиться острів Родос, у центрі якого на торговельній площі між морем і міськими воротами знаходиться статуя бога сонця Геліоса. Висота скульптури досягає 36 м, на її виготовлення Карет витратив 12 років. Приблизно через 50 років землетрусом статуя була зруйнована.

 

13

 

Щоб збудувати таку споруду, потрібно було розв’язати чимало математичних задач.

 

Вчитель математики. Отож ми з вами теж розв’яжемо завдання.  (Учням роздаю карточки з диференційованими завданнями).

КАРТОЧКА №1

Розв’яжіть систему рівнянь

x + y = 2,

x – y = 0       графічно.

 

КАРТОЧКА №2

Розв’яжіть систему рівнянь

x – y = 2,

3x – 2y = 9       методом додавання.

 

КАРТОЧКА №3

Розв’яжіть систему рівнянь

5x + 6y = 215,

7x + 3y = 166       методом додавання.

 

КАРТОЧКА №4

Розв’яжіть систему рівнянь

x + y = 3,

x – y = 1       графічно.

 

КАРТОЧКА №5

Розв’яжіть систему рівнянь

1x – 2y = 3,

5x + y = 4       методом підстановки.

 

КАРТОЧКА №6

Розв’яжіть систему рівнянь

2x + 3y = 165,

5x + 2y = 330       методом додавання.

 

КАРТОЧКА №7

Розв’яжіть систему рівнянь

x + y = 3,

y – x = 1        графічно.

 

КАРТОЧКА №8

Розв’яжіть систему рівнянь

x + 2y = 11,

5x – 3y = 3       методом підстановки.

 

КАРТОЧКА №9

Розв’яжіть систему рівнянь

5x + 7y = 57,

9x – 7y = 83      методом додавання.

 

14

4. РОЗВ’ЯЗУВАННЯ ВПРАВ

Вчитель культури.

 

Александрійський маяк

На острові Фарос вперше було збудовано маяк заввишки 118 м. Щоб кораблі обминали рифи на шляху до Александрійської бухти, весь час на вершині будівлі підтримувалося полум’я, яке за рахунок бронзового покриття було видне більш ніж на 50 км. Круглу терасу оточувала колонада, на якій була пірамідальна вежа, увінчана статуєю Посейдона. Простояв маяк 1500 років, а потім його було зруйновано. У наші часи на цьому місці знаходиться військовий форт мусульман.

Ми з вами живемо в мирній країні. Тож нехай у вашому житті буде лише “Математичний бій”.

 

Вчитель математики.

Математичний бій

 

Усна розминка команд:

• Чому дорівнює  2(3x – 4) + 5x =

                                 5 – 3(2x + 1) =

                                 3(2y –2) – 3y =

                                 8 – 2(y –4) =

 

Яка команда перша виконає завдання:

• Що є графіком лінійної функції?
• Що є розв’язком системи двох рівнянь з двома змінними?
• Чи буде пара чисел (5; 6) розв’язком системи

а)  x + y = -1,                          б)  2x – y = 4,

     x – y = 11 ;                              x + 2y = -8.

• Скільки розв’язків має система рівнянь?

а)     3x + 2y = 1,

   5x – 2y = 7;

 

б)   3x – 2y = 6,

   6x – 4y = 12;

 

  в)   5x – y = 1,

  10x – 2y = -3.

Змагання лідерів:

• №437 (а,б) у підручнику

 

Нам треба продовжувати подорож.  Отже ми  вирушаємо  до Галікарнасу.

 

5. ЗАВДАННЯ ДОДОМУ

Вчитель культури.

Мавзолей у Галікарнасі

У Галікарнасі  у давні часи правив цар Мавсол.  Ще за життя Мавсол почав будувати собі гробницю, яка вражала людей своєю величністю і поєднувала в собі грецький храм, башту, піраміду.                                                                                                    15

     36 іонійських колон, які тримали дах у вигляді двадцяти чотирьох ступінчастої піраміди, оточували мармуровий п’єдестал, де знаходився храм. Гробниця була названа Мавзолеєм на честь царя Мавсола. Це чудо світу увічнило кохання цариці Артемісії до свого померлого чоловіка. Після єгипетських пірамід ця споруда – найбільша серед гробниць. (Діти записують №№ варіантів у щоденники)

6. ПІДСУМОК УРОКУ

Вчитель математики.

Висячі сади Семіраміди.

Останньою зупинкою нашої подорожі є столиця країни, що знаходилась між річками Тигр і Євфрат. Це – Вавилон. З усіх Вавилонських чудес найвизначнішими вважають висячі сади Семіраміди. Сади розташовані на склепіннях, опертих на кам’яні брили, на які насипано товстий шар землі. Успіх садоводів полягав у досконалій системі поливу. У саду серед різних рослин було багато квітів. Букет квітів я хочу вам подарувати, але для цього прошу попрацювати.

• Які способи розв’язання систем ми використовували на уроці?
• Що є розв’язком системи рівнянь?
• Подорож до яких чудес світу ми з вами здійснили?

Пазл.

3	9	6
5	7	4
8	1	2

 

Оголошення та коментування оцінок.

16

АЛГЕБРА 7 клас

 

Тема. Множення многочлена на одночлен, многочлена на многочлен

 

Мета: формувати вміння множити одночлен на многочлен і многочлен на многочлен, складати алгоритми; застосовувати отримані теоретичні знання до розв’язування рівнянь і задач; перевірити в ігровій формі теоретичні знання і практичні навички й уміння з теми; активізувати роботу учнів за допомогою участі кожного в грі; розвивати логічне мислення учнів.

 

ХІД УРОКУ

 

І. Початок уроку

 

1. Домашнє завдання перевіряють учні (робота в парах). (Учні обмінюються зошитами і звіряють розв’язання з вивішеними розв’язаннями завдань на дошці.)

2. Фантастичне доповнення. (Клас розбивається на три команди.) Ми перебуваємо в космосі. Корабель спіткало нещастя. Двері заблоковані. Необхідно проникнути у відсік, де знаходиться ангар з міні-кораблями. Проникнути можна з трьох боків, відкриваючи почергово троє дверей. Правильна відповідь — це код кожних дверей.

 

(Вивішуються алгоритми: «Множення одночлена на многочлен» і «Множення многочлена на многочлен».)

 

 ІІ. Закріплення, тренування, відпрацьовування вмінь

 

1. «Лови помилку». Знайдіть помилку в розв’язанні прикладів: (Помилки на алгоритми множення раціональних виразів і дій зі степенями.)

             

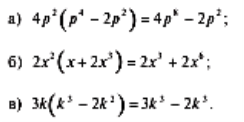
                                                                                                                                                                                                                                                                                       17

 2. Задача. Довжина прямокутника на 20 м більша від його ширини. Якщо довжину прямокутника зменшити на 10 м, а ширину збільшити на 6 м, то площа прямокутника збільшиться на 12 м 2 . Знайдіть довжини сторін прямокутника. У ході аналізу задачі під керівництвом учителя заповнюється таблиця:

 

 

Задача розв’язується в зошитах з повним поясненням.

Під керівництвом учителя пояснення обговорюється і пишеться в зошитах під коментар учнів. (Рівняння учні розв’язують самостійно. По завершенні роботи звіряються з розв’язанням, вивішеним на дошці).

ІІІ. Повторення

Свої  приклади.  Команда обмінюються прикладами (Вдома готують по 2 приклади: 1) на додавання многочленів; 2) на віднімання многочленів. Вивішуються алгоритми: «Додавання многочленів» і «Віднімання многочленів».)

 

ІV. Контроль Бліц-контрольна робота.

 

 

 

 

 

 

V. Домашнє завдання.  § 11, 12 — повторити, № 191, 192, 195, 211, 226 — розв’язати. (Необхідний мінімум: будь-які два варіанти з № 191, 192,211, задача 226).

 

VI. Кінець уроку.

 Опитування-підсумок.

Питання до класу:

1. Що на уроці було головним?

2. Що на уроці було цікавим?

3. Чого сьогодні ми навчилися?

 

 

 

18

                                            ,                                                                                                                                                               

 

 

 

 

 

 

                                         

 

ХIД УРОКУ

 

І. Органiзацiйний етап, мотивація навчальної діяльності

     Сьогодні ми продовжуємо подорож у країну Десяткових Дробів. Під час подорожі повторимо все, що вже знаємо про десяткові дроби: що таке десятковий дріб; як порівнювати десяткові дроби; як додавати й віднімати десяткові дроби; які закони діють під час додавання десяткових дробів. А подорожувати ми сьогодні будемо на веселому Математичному трамвайчику (плакат із  зображенням трамвайчика висить на дошці). Ви бажаєте покататися на цьому трамвайчику? Для цього вам треба купити квиток. Але квиток тут можна одержати не за гроші, а за правильну вiдповiдь на запитання або за правильно виконане завдання. Ви готові до подорожі? Водієм трамвайчика буду я, а кондуктором — мій помічник (учень 9 кл). Отже, починаємо набирати пасажирів.

 

ІІ. «Купівля квитків»

 

 Фронтальне опитування

1. Що таке десятковий дріб?

2. З яких частин складається десятковий дріб?

3. За яким принципом записують десятковий дріб?

4. Як порівняти два десяткових дроби? Наведіть приклад.

5. Як додати два десяткових дроби? Наведіть приклад.

6. Які властивості має додавання десяткових дробів i для чого вони нам потрібні?

7. Як відняти два десяткових дроби? Наведіть приклад.

8. Який знак треба поставити поміж числами 5i 6,щоб дістати число, більше ніж 5 i менше ніж 6?

Учні, які правильно відповідають на запитання, одержують квиток – червоний прямокутник. Отже, є перші пасажири, тож починаємо подорож.

 

ІІІ. «Подорож у країну Десяткових Дробів»

 

Перша зупинка «Виправ помилку» (усна робота)

 

19

     З нами у подорож напросився Незнайко, він навіть склав для вас кілька прикладів на додавання й віднімання десяткових дробів, але, як завжди, щось наплутав i одержав якісь смішні рівності. Допоможіть їх виправити.

(За правильну вiдповiдь – червоний прямокутник - квиток). Наш трамвайчик поповнився ще пасажирами, й ми поїхали далі.

 

Друга зупинка «Магічна»

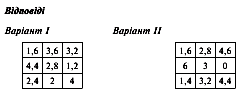
     На цій зупинці на нас чекає зустріч iз магічними квадратами. Що ви про них знаєте? (На дошці заздалегідь намальовано 2 квадрати iз пропущеними клітинками.)

(Робота на два варіанти (самостійно), кондуктор (помічник) перевіряє правильність заповнення магічних квадратів.) Перші шість учнів (по одному з кожного ряду), які правильно заповнили квадрати, одержують квиток — червоний прямокутник.

Потім представники від кожного варіанта заповнюють пропущені клітинки квадратів, а учні себе перевіряють. Ми вітаємо нових пасажирів нашого трамвайчика та їдемо далi.

 

Третя зупинка «Пошукова»

     Одного разу в англійському графстві Камберленд почалася гроза, сильний вітер виривав дерева з корінням, утворюючи вирви. В одній iз таких вирв жител виявили якусь чорну речовину. Давайте з’ясуємо, що це була за речовина. А для цього розв’яжемо рівняння, оскільки назву речовини можна визначити, якщо замінити корені цих рівнянь вiдповiдними літерами з таблиці (на дошці заздалегідь заготовлено таблицю).

 

20

 

     Учні розв’язують рівняння самостійно, два учні — за дошкою. Потім проводиться перевірка. Якщо на дошці є помилка, то учень, який помітив, її виправляє й одержує червоний прямокутник - квиток на трамвайчик, а той, хто припустився помилки,— синій прямокутник - квиток.

 

Дістали слово – «графіт»

 

     Шматочками графіту пастухи почали мітити овець, а торговці робити написи на кошиках i ящиках. І трапилося це в 1565 році. Скажіть, у якому столітті був винайдений графіт?

     Перші олівці мали два недоліки: вони бруднили пальці й швидко ламалися. Шматки графіту почали обмотувати тасьмою, тканиною, а для міцності змішували iз сіркою, смолою, сурмою. Пізніше стали додавати глину й суміш обпалювали в печі. Такий    олівець,якими ми пишемо сьогодні з’явилися  наприкiнцi XVIII століття. Ви, напевно, уже трохи втомилися, i тому наш трамвайчик зробить зупинку.

 

Четверта зупинка «Спортивна»

     На цій зупинці ви позмагаєтеся у грі «Хто швидше». Кожний ряд одержує картку (завдання) й ланцюжком виконує по одному завданню з картки, передаючи її далi. Перемагає той ряд, який найшвидше й правильно виконає завдання (усі учні цього ряду одержують червоний прямокутник - квиток). Замість зірочок запишіть таку цифру, щоб утворилася правильна нерiвнiсть

     Перевіряє правильність виконання завдання кондуктор трамвая – помічник учителя.

 

П’ята зупинка «Історична»

     Поки триває перевірка, вчитель розповідає про історію виникнення десяткових дробів. Середньоазіатське місто Самарканд (Узбекистан) у XV столітті було великим

21

 

культурним центром. Там, у знаменитій обсерваторії, створеній астрономом Улугбеком, онуком монгольського володаря Тамерлана, працював                                       у 200х роках XV сторіччя великий учений того часу – Джемшид Гияседдин аль - Кашi.                              

Це він уперше виклав учення про десяткові дроби. Аль - Кашi сформулював правила й навів приклади дій iз десятковими дробами. Він запропонував специфічний для десяткових дробів запис: цілу й дробову частини записувати в одному рядку. Для відокремлення першої частини від дробової не застосовував коми, а записував цілу частину чорним чорнилом, дробову ж — червоним або відокремлював цілу частину від дробової вертикальною рискою. Близько 150 років після аль - Кашi в Європі вчення про десяткові дроби вперше виклав фламандський інженер i вчений Симон Стевiн (1548–1620). У 1585 році він написав невелику книгу за назвою «Десята». Вона складалася лише iз 7 сторінок, однак містила в повному обсязі теорію десяткових дробів. Запис десяткових дробів у Стевiна був відмінним від нашого. На початку XVII століття починається досить інтенсивне проникнення десяткових дробів у науку й практику. В Англії в якості знака, що відокремлює цілу частину вiд дробової, було введено крапку, яку й понині використовують для цього в США, Англії та деяких інших країнах. Кому, як i крапку, в якості розділового знака запропонував                      у 1616–1617 роках знаменитий англійський математик Джон Непер. Розвиток промисловості й торгівлі, науки й техніки вимагали більш громіздких обчислень, які за допомогою десяткових дробів легше було виконати. У Росiї вчення про десяткові дроби вперше виклав у своїй «Арифметиці» Леонтій Магницький (1703). Найширшого застосування десяткові дроби одержали в XIXст., після введення тісно пов’язаної з ними метричної системи мiр i ваги. У сільському господарстві й промисловості нашої країни, в науці й у всіх галузях народного господарства десяткові дроби й деякі їх види, відсотки, застосовуються набагато частіше, ніж звичайні дроби.

 

Шоста зупинка «Пізнавальна». Учні виконують самостійну роботу.

Варіант І

Розташуй відповіді прикладів у порядку зростання, i ти дізнаєшся назву металу, який плаває у воді й не тоне.

Вiдповiдь. Лiтiй.

 

Варіант ІІ

 Розташуй відповіді прикладів у порядку спадання, i ти дізнаєшся назву найміцнішого металу.

 

Вiдповiдь. Титан.

     Вiдповiдi заздалегідь записано на дошці. Кондуктор - помічник перевіряє відповіді в учнів, які першими виконали завдання, й дає їм червоний прямокутник — квиток на математичний трамвайчик.

22

     Про властивості цих металів та їх використання ви дізнаєтеся на уроках хімії.

 

 VІ. Підбиття підсумків уроку

     Ось i добігла кінця наша подорож. Чим же ми займалися під час подорожі? Що нового дізналися? Кожний учень рахує свої червонi квитки. Найактивнішим «пасажирам» виставляються оцінки. Оцінки також одержують тi учні, які розв’язували на дошці рівняння, й тi, які правильно виконали самостійну роботу з картки.

 

V. Домашнє завдання

1. Порівняйте:

1) 14,396 та 14,4;  2) 0,657 та 0,6565.

 2. Округліть:

1) 16,76 до десятих;  2) 0,4864 до тисячних.

3. Виконайте дії:

1) 3,87 +  32,496;  2) 23,7 – 16,48;  3) 20 – 12,345.

4. Швидкість катера за течією річки дорівнює 24,2 км/год, а власна швидкість катера — 22,8 км/год. Знайдіть швидкість катера проти течії річки.

 5. Обчисліть, записавши величини в кілограмах:

1) 3,4 кг + 839 г;  2) 2 кг 30 г – 1956 г.

6. Одна зi сторін трикутника дорівнює 5,6 см, що на 1,4 см більше від другої сторони на 0,7см менше від третьої. Знайдіть периметр трикутника.

 7. Напишіть три числа, кожне з яких більше від 5,74 i менше за 5,76.

8. Знайдіть значення виразу, вибираючи зручний порядок обчислення:

1) (8,63 + 3,298) – 5,63;

2) 0,927 – (0,327 + 0,429).

 

 

 23

Урок з алгебри та геометрії

 

 

Підсумкове  повторення програмного матеріалу

з алгебри та геометрії 8 клас

 

Мета: Перевірити учнів застосовувати набуті знання у нестандартних ситуаціях, мобілізувати учнів на активне оволодіння програмним матеріалом, розвивати логічне мислення учнів, пам'ять, увагу, самостійність, формувати інтерес до            математики.

 

Форма проведення: конкурс « Зірка математики ».

 

Девіз: Математика вчить мислити й разом з тим

           вселяє віру в безмежні сили людського розуму.

           Вона виховує волю, характер.

 

Обладнання: Геометричні фігури різного кольору для проведення психологічного тренінгу, картки з питаннями трьох турів, таблиця  результатів, картки для відповідей,                        картки для виявлення вражень від уроку.

 

ХІД УРОКУ

 

І. Організаційний момент

 

     Тема нашого сьогоднішнього уроку: «Підсумкове повторення програмного матеріалу з алгебри та геометрії за 8 клас». Проведемо ми наш урок в формі конкурсу, який називається «Зірка математики». В кінці нашого уроку переможець буде нагороджений заохочувальним призом. Підраховувати кількість правильних відповідей буде наша суддівська колегія, яка складається з трьох учнів 10-А класу. Кількість балів, які ви наберете буде внесено до таблиці результатів. Девіз нашого уроку: «Математика вчить мислити й разом з тим вселяє віру в безмежні сили людського розуму. Вона виховує волю, характер». Давайте ознайомимося з планом сьогоднішнього уроку:

  І. Психологічний тренінг.

ІІ. Перший тур.

ІІІ. Математична  розминка.

ІV. Другий тур.

V. Екскурс до енциклопедії.

VІ. Третій тур.

VІІ. Продовження екскурсії.

VІІІ. Підведення підсумків, рефлексія.

ІХ. Нагородження.

 

     Правила нашого конкурсу: за п’ять хвилин треба дати відповіді на дванадцять запитань, які ви вписуєте в картки. По закінченню п’яти хвилин суддівська колегія збирає картки з відповідями і перевіряють правильність виконання завдань. За математичну розминку можна отримати додаткові бали, які будуть враховуватися в загальну кількість балів.

24

І. Психологічний тренінг

 

 Перед початком першого туру давайте перевіримо на скільки психологічно ви готові до уроку. Для цього візьміть будь ласка аркуші паперу, які лежать у вас на партах. За 30 секунд вам треба написати вертикальні рисочки розміром до одного сантиметру. Після цього підрахувати кількість рисочок, помножити на 100% і поділити на 156. Якщо ви отримали від 0 до 33 відсотків – низький рівень готовності, ви піднімаєте зелений квадрат, якщо ви одержали від 33 до 66 відсотків – середній рівень готовності, піднімаєте жовтий трикутник. Якщо ж ви одержали від 66 до 100 відсотків – високий рівень готовності – червоний кружок.

Після проведення психологічного тренінгу видно, що більшість учнів має високий рівень готовності до уроку.

 

ІІ. Перший тур

 

     Тепер ми можемо перейти до проведення нашого сьогоднішнього конкурсу. Приготуйте карти із запитаннями зеленого кольору і картки для написання відповідей. За п’ять хвилин вам треба дати відповіді на дванадцять запитань.

 

Доки учні виконують завдання в класі звучить тихенька заспокійлива музика, яка дає змогу сконцентрувати увагу.

 

Питання першого туру.

 

1. Відрізок має:

а) початок і не має кінця;

б) має початок і кінець;

в) немає ні початку ні кінця;

г) початок і кінець збігається.

 

2. Рівнобе6дрений трикутник, в якого сторони рівні:

а) три; 

б) ні одної;

в) дві;

г) основи.

 

3. Площа квадрата обчислюється за формулою:

а) S=a;

б) S=a²;

в) S=a³;

г) S=2a.

 

4. Прямокутний трикутник має:

а) один прямий кут;

б) два прямі кути;

в) три;

г) жодного.

 

 

 

 

25

5. Парабола задається формулою:

а) у=х;

б) y=kx+b;

в) y=b;

г)y=x².

 

6. При множенні степенів з однаковими основами степені:

а) віднімаються;

б) перемножуються;

в) додаються;

г) діляться.

 

7. Як називається відрізок, що сполучає вершину трикутника з серединою протилежної сторони цього трикутника:

а) бісектриса;

б) медіана;

в) висота;

г) перпендикуляр.

 

8. Косинус кута це відношення:

а) катета прилеглого до протилежного;

б) прилеглого катета до гіпотенузи;

в) протилежного до гіпотенузи;

г) протилежного до прилеглого.

 

9. Через точку, що лежить на даній прямій, можна провести на площині прямих, паралельних даній:

а) одну;

б) дві;

в) жодної;

г) безліч.

 

10. дорівнює:

а) 0;

б) 1;

в) 2;

г) -1.

 

11. Довжина звичайного олівця:

а) 100 мм;

б) 188 мм;

в) 75 мм;

г) 315 мм.

 

12.  Скільки буде коли 10 поділити на десяту частину:

а) 10;

б) ;

в) 100;

г) 0,1.                                                                                                                   26                

ІІІ. Математична розминка

 

 Суддівська колегія підраховує кількість балів, а ми  поки що відволічемося і порозв’язуємо задачки.

 

Розминка

1. На дереві сиділо 6 горобців. Стрілець, вистріливши, влучив у двох із них. Скільки горобців залишилося на дереві?

а) 4;

б) 2;

в) 6;

г) жодного.

2. Одне яйце варять протягом 4 хвилин. Тоді воно вважається звареним. За скільки хвилин можна зварити п’ять яєць?

а) за 5 хвилин;

б) за 20 хвилин;

в) за 10 хвилин;

г) за 4 хвилини.

3.  У батька 5 дочок і кожна дочка має брата. Скільки дітей у батька?

а) 10;

б) 6;

в) 5;

г) 12.

4. Садівника спитали, скільки в твоєму саду дерев? Він відповів: «Половина всіх моїх дерев – яблуні, половина тих, що залишилася – груші, решта – шість дерев - вишні». Скільки в цьому саду дерев?

а) 6;

б) 3;

в) 12;

г) 24.

 

Додаткові запитання:

1.Хто із вчених-математиків був першим астрономом?

 а) Декарт;

 б) Піфагор;

 в) Евклід;

 г) Фалес.

2. Вкажіть імя єдиної жінки, учениці Піфагора:

 а) Гепатія;

 б) С. Ковалевська;

 в) Теано;

 г) Гортензія Лепот.

3. Кого з великих математиків назвали «батьком алгебри»?

 а) Гаусса;

 б) Галуа;

 в) Вієта;

 г) Декарта.

27

4. «Трудова книжка» учня:

 а) зошит;

 б) щоденник;

 в) підручник;

 г) табель.

5. Коли день рівний ночі на всій Землі, крім полюсів?

 а) 22 червня;

 б) 20 квітня;

 в) 22 грудня;

 г) 23 вересня.

6. Яке число у Древньому Вавілоні вважалося священним?

 а) 3;

 б) 7;

 в) 10;

 г) 12.

7. Яке число називають «чортовою дюжиною»?

 а) 12;

 б) 7;

 в) 13;

 г) 16.

8. Скільки днів має високосний рік?

 а) 360;

 б) 365;

 в) 366;

 г) 369.

 

Поглянемо чи є у нас лідери після першого туру? За розминку учні, які дали правильні відповіді на запитання отримують по одному балу.

 

ІV. Другий тур

 

 Настав час перейти до другого туру нашого конкурсу. Приготували картки синього кольору і картки для відповідей.

 

Доки учні виконують завдання в класі звучить тихенька заспокійлива музика, яка дає змогу сконцентрувати увагу.

 

Питання другого туру

1. Прямий кут дорівнює:

а) 180º;

б) 130º;

в) 70º;

г) 90º.

2. Перпендикулярні прямі перетинаються під:

а) прямим кутом;

б) гострим;

в) тупим;

г) розгорнутим.

28

3. Діаметр дорівнює радіусам:

а) одному;

б) двом;

в) трьом;

г) ні одному.

 

4. Гострокутний трикутник має гострих кутів:

а) один кут;

б) два;

в) три;

г) жодного кута.

 

5.  Лінійна функція задається формулою:

а) y=kx;

б) y=kx+b;

в) y=kx²+b;

г) y=x²+b.

 

6. При діленні степенів з однаковими основами степені:

а) додаються;

б) віднімаються;

в) діляться;

г) перемножуються.

 

7. Сума кутів трикутника дорівнює:

а) 90°;

б) 180°;

в) 120°;

г) 360°.

 

8. Синус кута - це відношення:

а) протилежного катета до гіпотенузи;

б) прилеглого катета до гіпотенузи;

в) гіпотенузи до протилежного катета;

г) гіпотенузи до прилеглого катета.

 

9. Кравець має кусок сукна 18 м і щодня відрізає від нього по 3 м. На який день він це зробить в останній раз:

а) 3;

б) 5;

в) 6;

г) 7.

 

10. Скільки буде коли сотню поділити на четверту частину?

а) 25;

б) 50;

в) ¼;

г) 400.

29

11. Швидкість течії річки 1,5 км/год. Пароплав пливе проти течії річки. На скільки кілометрів за годину його швидкість за течією буде більша від швидкості проти течії?

а) 1,5 км/год;

б) 2,5 км/год;

в) 3 км/год;

г) 0,7 км/год.

 

12. У якій країні дроби називали «ламаними числами»?

а) Стародавня Русь;

б) Німеччина;

в) Англія;

г) Стародавня Греція.

 

V. Екскурс до енциклопедії

 

Чи знаєте ви жінок-математиків? Якщо знаєте назвіть їх. Чи можете розказати про них?

Вчитель .Я бачу ніхто з вас не володіє такою інформацією. Тому я познайомлю вас з видатною жінкою-математиком і трохи розповім про неї.

Софія Ковалевські.

Перша російська жінка-математик Софія Василівна Ковалевські народилася в Москві в багатій родині. Дівчинка зростала різнобічно здібною, але особливо її цікавила математика. Перше знайомство з математикою відбулося у 8 років. Коли для по клеєння кімнати не вистачило шпалер і стіни кімнати було поклеєні лекціями М. В. Остроградського з математичного аналізу. З 15 років вона почала вивчати курс вищої математики. В ті часи жінкам було заборонено навчатися в університетах і для того щоб виїхати за кордон і отримати там освіту вона фіктивно одружується з молодим ученим-біологом В. О. Ковалевським.

В 1869 році  подружжя виїжджають  до Германії. Ковалевська займається індивідуально з німецьким вченим К. Вейєрштрасса, тому що жінок не приймали до університетів. В 1874 році вона отримує ступінь доктора філософії і повертається до Петербургу.

В 1880 році  Ковалевська  переїжджає до Москви, але їй забороняють здавати в університеті магістерські екзамени. Вона переїжджає до Парижу де їй також не посміхається доля. Тільки в 1883 році в Швеції вона починає працювати в Стокгольмськім університеті, де і стає професором. Цей період став розквітом наукової діяльності. В 1888 році вона написала роботу «Задачі про обертання твердого тіла навколо нерухомої точки» за яку отримала премію Паризької академії наук – премія Бордена. С. В. Ковалевські мрія про наукову роботу в Росії, але її мрія не здійснилася, в 1891 році вона померла в Стокгольмі.

Кількість балів  підрахована і ми бачимо, що у нас є два лідера, але попереду ще один тур. І ситуація може змінитися. Тому кожен з вас має шанс стати переможцем.

 

VІ. Третій тур

 

Настав час перейти до третього туру нашого конкурсу. Приготували картки жовтого кольору і картки для відповідей.

30

Доки учні виконують завдання в класі звучить тихенька заспокійлива музика, яка дає змогу сконцентрувати увагу.

 

Питання третього туру

 

1. Тупий кут – це :

а) 170º;

б) 180º;

в) 30º;

г) 90º.

 

2. Сума внутрішніх кутів чотирикутника…

а) 180º;

б) 100º;

в) 360º;

г) 270º.

 

3. Хто з великих математиків вперше наближено обчислив діаметр Землі?

а) Вієт;

б) Евклід;

в) Ератосфен;

г) Піфагор.

 

4. При скороченні дробів на одне число…

а) ділиться чисельник;

б) множиться знаменник;

в) ділиться знаменник і чисельник;

г) множиться знаменник і чисельник.

 

5. Тупокутий трикутник має:

а) один тупий кут;

б) два;

в) три;

г) жодного.

 

6. Ромб у якого сторони рівні:

а) дві;

б) три;

в) чотири;

г) жодної.

 

7. Теорема Піфагора:

а) різниця квадратів катетів дорівнює квадрату гіпотенузи;

б) сума квадратів катетів дорівнює квадрату гіпотенузи;

в) сума катетів дорівнює гіпотенузі;

г) різниця катетів дорівнює гіпотенузі.

 

 

 

 

 

31

8. tg – це відношення:

а) прилеглого катета до гіпотенузи;

б) протилежного катета до гіпотенузи;

в) прилеглого катета до гіпотенузи;

г) протилежного до прилеглого.

 

9. Двоє пішли – 3 гвіздка знайшли, слідом четверо йдуть. Скільки гвіздків знайдуть?

а) 3;

б) 4;

в) 6;

г) жодного.

 

   10. В якому трикутнику сума двох його кутів дорівнює третьому?

а) гострокутному;

б) прямокутному;

в) тупокутному;

г) рівнобедреному.

 

  11. Годинник б’є кожну годину і відбиває стільки ударів, скільки

    показує годинникова стрілка. Скільки ударів відбиває

    годинник протягом 12 годин?

а) 12;

б) 36;

в) 78;

г) 24.

 

  12. Яка маса учнівського зошита в 12 аркушів?

а) 500 г;

б) 75 г;

в) 100 г;

г) 35 г.

 

Роботи здані для перевірки.

 

VІІ. Продовження екскурсії

 

     Ось ми і пройшли всі три туру нашого конкурсу. Поки підраховується кількість балів за третій тур і загальна кількість балів ми продовжимо екскурсію до енциклопедії.

 Чим захоплювалися вчені-математики?

 

Учні наводять приклади чим  могли цікавитися вчені окрім математики.

 

Вчитель. 548 року до н. е. на 58 Олімпіаді в кулачних боях брав участь великий математик Піфагор. Але були й такі математики-вболівальники які помирали на Олімпійських іграх.

Вчитель. Були і трагічні випадки в житті математиків. Так на 59 Олімпійських іграх під час бою Піфагора помер знаменитий вчений Фалес Мілетський.                           32

Були й інші випадки в історії коли вчені-математики гинули на дуелях. Таким вченим був Галуа.

 

VІІІ. Підведення підсумків, рефлексія

 

     Поки суддівська колегія заповнює таблицю результатів давайте перевіримо чи не змінився ваш психологічний стан під час уроку.

 

      Учні піднімають геометричні фігури і видно, що їхній стан не змінився. У них високий рівень психологічної готовності.

       Напишіть будь ласка ваші враження від уроку і побажання на майбутнє.

 

ІХ. Нагородження

 

 

 

 

 

 

33

Зміст

 

 

1.  Дидактичні ігри на уроках математики……………………………1
2. Розробки уроків з елементами дидактичних ігор…………………8

Логічний олімп……………………………………………………….8

Подорож до семи чудес світу…………………………………......11

Космічна подорож…………………………………………………..17

Подорож на «математичному трамвайчику»…………………….19

Зірка математики……………………………………………………24

3. Зміст…………………………………………………………………34

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2012