З досвіду роботи "Розвиток творчих здібностей школяра на уроках математики. Формули скороченого множення"

 

 

 

 

 

Розвиток творчих здібностей школяра на уроках математики. Формули скороченого множення

 

 

Підготувала

Гавриль Мар’яна Федорівна,

вчитель математики

Мерешорського НВК І-ІІст.

Міжгірського району

 

 

 

 

 

 

 

Зміст

 

Вступ…………………………..……………………………………………...3

1. Особливості розвитку творчих здібностей на уроках математики..…..4

1.1. Умови успішного розвитку творчих здібностей особистості……......4

1.2. Основні показники творчих здібностей……………………………….7

1.3. Поняття математичних здібностей…………………………………….7

2. Засоби розвитку творчих здібностей школярів на уроках математики….……………………………………………………………………... 8

2.1. Нестандартні уроки – як акцентуація розвитку творчих здібностей………………………………………………………………….……….9

2.2. Роль і місце дидактичних ігор на уроках математики………………11

2.3. Проблемні задачі – як засіб розвитку творчих здібностей школяра…………………………………………………………………………..12

3. Формули скороченого множення, їх застосування у математиці…………………………………………………...............................…14

Висновки ………………………………………………………………….21

Список використаної літератури………………………………………...22

 

 

 

 

 

 

Вступ

Математика є одним із найскладніших предметів у школі. Вивчаючи математику учні формують не лише предметні компетенції: знання, вміння, навички а й пізнавальний інтерес, логічне мислення, творчу уяву. Вона сприяє виробленню особливого виду пам'яті – пам'яті, спрямованої на узагальнення, творення логічних схем, формалізованих структур, виховує здатність до просторових уявлень. Саме тому наявність математичних здібностей в одних учнів і недостатня розвинутість їх в інших вимагає від учителя постійного пошуку, шляхів формування і розвитку таких здібностей у школярів.

Творчість учнів сприяє формуванню їхніх морально-етичний та вольових якостей. Творча діяльність школярів позначається на їхньому фізичному та естетичного розвитку.Залучення учнів до творчої діяльності розкриває перед ними горизонти людських можливостейісприяє правильному визначенню свого місця на широкому полі Власних знань, умінь та здібностей. Відбувається це з тієї причини, що в творчості людина реалізує в усій повноті свої знання, уміння та здібності, а отже, отримавшиможливість випробувати себе в різних видах діяльності, наочно переконується в наявному арсеналі знань, умінь та здібностей, адекватно оцінюючи свої можливості, що, безумовно, сприяє правильному вибору професії.

Розвиваючі творчі здібності школярів, залучаючи їх до творчої діяльності, створюючи умови для реалізації їхніх творчих можливостей, можна вберегтиїх від моральної деградації. Розвиток творчих здібностей школярів обумовлюється також зацікавленістю держави у високій трудовій активності своїх громадян. Із підвищеною трудовою активністю тісно пов'язані продуктивність та якість праці. Вищим рівнем розвитку трудової активності є творча активність, яка за своєю суттю полягає у постійному прагненні нарощуватипродуктивність та підвищуватиякість праці, що неможливо без глибокого проникнення в сутність трудового процесу ійого вдосконалення, тобто без розвинення до певного рівня творчих здібностей індивідуума.

1. Особливості розвитку творчих здібностей на уроках математики

1.1. Умови успішного розвитку творчих здібностей особистості

Проблема розвитку творчих здібностей особи є однією з центральних в педагогіці, оскільки прогрес суспільства – це шлях постійної творчості, долання стереотипів і вироблення нових, нестандартних, часто несподіваних ідей, оригінальних підходів і шляхів до їх втілення. Одним з головних педагогічних завдань при цьому є виховання людини, здатної акумулювати і творчо переосмислювати набутий досвід, досягнення людства в науці, культурі, мистецтві, розвивати технології. Кожна дитина поступово приходить до багатьох результатів шляхом кропіткої роботи. Одному це дається легше іншому – складніше. Але кожний наступний крок, який зробить учень, заслуговує на похвалу. Важливо, щоб учня запевнили в тому,що вона здатна на більше.

Щоб керувати розвитком розумових дій, цілеспрямовано формувати якості творчої особистості і творчі здібності, треба знати, про які саме якості йде мова. А. Н. Лук до творчих здібностей відносить:

– здатність до згортання розумових дій (здатність до заміни кількох понять одним, до використання більш ємних в інформаційному плані символів);

– здатність до переносу досвіду (це здатність до вироблення узагальнюючих стратегій);

– наближення понять (здатність асоціювання віддалених асоційованих понять);

– гнучкість мислення (здатність легко й швидко переходити від одного класу явищ до іншого, далекого за змістом);

– здатність до оцінювання (вибір однієї із багатьох альтернатив до її перевірки, тобто на різних етапах і стадіях творчого процесу);

– легкість генерування ідей [2].

Природа щедро наділила кожну здорову дитину можливостями для розвитку. І кожен учень може піднестися до найбільших висот творчої діяльності! Але в житті ми бачимо зовсім інше: а скільки ще сліз ллють школярі, яким важко вчитися, а скільки гірких хвилин переживають батьки, коли з навчанням у дітей погано! Треба створити у школі таке середовище і таку систему взаємин, які стимулювали б найрізноманітнішу діяльність дитини, поступово розвивали б у неї саме те, що в даний момент може найефективніше розвиватися.

Саме це і є  першою важливою умовою ефективного розвитку здібностей. Передусім для розкриття здібностей учнів необхідно створити в класі творчу, доброзичливу, емоційно позитивну атмосферу

Завдання вчителя на уроці – бути водночас і дорослим, і дитиною, а найголовніше – бути спокійним, доброзичливим.

Друга умова успішного розвитку творчих здібностей випливає із самогохарактеру творчого процесу, який потребує максимального напруження сил. Здібності розвиваються тим успішніше, чим частіше дитина підходить у своїй діяльності до межі власних можливостей, поступово відсуваючи цю межу все далі. Процес пізнання в цей час дуже інтенсивний, дитина змушена займатися творчістю, розв’язувати багато нових завдань самостійно, без попереднього навчання. Саме ця інтенсивна розумова діяльність допомагає учневі в дивовижно короткий час перетворитися на невтомногоЧомучку .

Третя умова. Треба давати учневі свободу вибирати вид діяльності, визначати черговість справи, тривалість занять певною справою, вибирати способи розв’язання завдань. Бажання дитини, інтерес, емоційне напруження інтелекту піде їй на користь

Надана дитині свобода не лише не заперечує, а передбачає ненав’язливу розумну, доброзичливу допомогу вчителя – це четверта умова успішного розвитку творчих здібностей. К. Ціолковський казав: «Спочатку я відкрив істини, відомі багатьом, потімпочав відкривати й істини відомі декому, і, нарешті, почав відкривати й істини нікому ще не відомі». Мабуть, це і є шлях становлення творчої складності інтелекту, шлях розвитку винахідницького і дослідницького таланту. Наш обов’язок – допомогти дитині стати на цей шлях.

Співпраця між учнями та вчителем, залучення батьків до організації і проведення різних форм роботи – запорука успішної роботи .

Постійно створюючи «ситуацію успіху», об’єднавши все повагою до особистості дітей , ми можемо розвинути таланти, творчі здібності всіх дітей, виховати творчих працюючих особистостей .

На уроках доцільно використовувати діяльно-творчий підхід, при якому формування особистості може відбуватися тільки в творчій діяльності.

На тих уроках, де діти відразу бачать результат своєї праці і знають, що їх робота потрібна, вони працюють із захопленням. Тому варто учнів залучати до пошуково-пізнавальної творчої роботи на основі співпраці.

Тому важлива роль відводиться інноваційним методам навчанням. Під час таких уроків дитина має право не тільки отримувати певну суму знань, уміти їх використовувати, а й розвивати свої творчі здібності, розвиватись як особистість. Для цього необхідні вимоги: науковість, зв’язок з життям, систематичність і послідовність, освітній, виховний і розвивальний вплив. Щоб розвивати творчий емоційний розвивальний процес навчання, необхідно застосовувати у практиці пізнавальні ігри, нестандартні форми проведення уроків, інноваційні методи навчання. Навчати учнів аналізувати життєві ситуації на основі вивчення легенд, казок, прислів’їв, скоромовок, оповідань, пісень. Важливо створити ті ситуації, з яких учні повинні самостійно знайти вихід або з допомогою своїх товаришів і вчителя. На основі цього учень створює для свого героя твору інший позитивний вихід із даної ситуації.

В процесі навчання важливо забезпечити виникнення позитивних емоцій стосовно навчальної і творчої діяльності.

Розвиток творчості починайте із створення ситуації, що сприяє інтуїтивному схопленні ідеї вирішення творчої проблеми. Ця творчість закінчується формуванням необхідних здібностей, створення творчого клімату, креативних якостей особистості.

1.2. Основні показники творчих здібностей

Основними показниками творчих здібностей є швидкість і гнучкість думки, оригінальність, допитливість, точність і сміливість.

Швидкість думки - кількість ідей, що виникають в одиницю часу.

Гнучкість думки - здатність швидко і без внутрішніх зусиль переключатися з однієї ідеї на іншу, бачити, що інформацію, отриману в одному контексті, можна використати в іншому.

Гнучкість - це добре розвинений навик переносу. Вона забезпечує вміння легко переходити від одних явищ до інших, своєчасно відмовлятися від скомпрометованого припущення, бути готовим до інтелектуально, ризику.

Оригінальність – здатність мислити нестандартно, здатність приймати рішення, що відрізняються від загальноприйнятих, парадоксальних, несподіваних. 

Допитливість - здатність дивуватися, цікавість і відкритість до всього нового.

Точність - здатність удосконалювати ідеї, надавати закінчений вигляд свого творчого продукту.

Сміливість - здатність приймати рішення в ситуації невизначеності, не лякатися власних висновків і доводити їх до кінця.

Чи є ці показники вродженими або ж вони можуть піддаватися впливу середовища? Один з творців системи вимірювання творчихздібностей - Торренс– говорив з цього приводу, що спадковий потенціал не є найважливішим показником майбутньої творчої продуктивності. В якій мірі творчі імпульси дитини перетворяться в творчий характер, залежить більше від впливу батьків та інших дорослих.

 

1.3. Поняття математичних здібностей

Математичні здібності – це здатність утворювати на математичному матеріалі узагальнені, згорнуті, гнучкі й обернені асоціації та їх системи. До складових математичних здібностей слід віднести:

* здатність до формалізації математичного матеріалу, відокремлення форми від змісту, абстрагування від реальних ситуацій і їх кількісних відношень та просторових форм; оперування структурами відношень і зв'язків;

*здатність до узагальнення матеріалу;

* здатність до оперування числовою і знаковою символікою;

* здатність до логічних міркувань, пов'язаних з потребою доводити, робити висновки;

* здатність до скорочення процессу міркувань;

* здатність до переходу від прямого до оберненого ходу думки;

*гнучкість мислення незалежно від впливу шаблонів.

Математика сприяє виробленню особливого виду пам'яті – пам'яті, спрямованої на узагальнення, творення логічних схем, формалізованих структур, виховує здатність до просторових уявлень. 

Наявність математичних здібностей в одних учнів і недостатнярозвинутістьїх в інших вимагає від учителя постійного пошуку, шляхів формування і розвитку таких здібностей у школярів.

Рівнева диференціація та розвивальне навчання з урахуванням психології математичних здібностей учнів збільшує можливості роботи вчителя. Такий підхід створює умови для розвитку здібностей учнів, які мають природжені задатки до занять математикою, і забезпечує посильною роботою учнів, які не мають таких задатків. Виконуючи посильні завдання, учень отримує впевненість у своїх силах.

 

2. Засоби розвитку творчих здібностей школярів на уроках математики

Щоб розвинути творчі здібності учнів, поступово та систематично залучати їх до самостійної пізнавальної діяльності, щоб забезпечити співпрацю між учнями та вчителем, традиційного уроку недостатньо. Отже, школа покликана розвивати творчі здібності буквально в усіх своїх вихованців, зважаючи, звичайно, на тих, які народжені з дещо різними задатками творити. В. Сухомлинський так відзначав мету шкільного навчання: розумові сили і здібності дитини мають постійно збагачуватися й розвиватись, а міцні знання вони матимуть лише тоді, коли не залишатимуться на одному й тому ж рівні розумових сил та здібностей. Сьогодні дитина має буті розумнішою, ніж вона була вчора, - тільки за цієї умови у неї буде бажання вчиться, і вона матиме успіх у навчанні. Можна стверджувати, що творче математичне мислення розпочинається з процесу розуміння умови математичної задачі за допомогою суб'єктивного переформулювання задачі на свою мову, це сприяє виділенню орієнтирів у задачі, що за своєю сутністю є качаном процесу формування гіпотези розв'язку, який спрямовується провідною ідеєю, що виникає, розвивається і наповнюється змістом в ході пошукової діяльності. Під дією провідної ідеї утворюється логічній ланцюг міркувань, який розпочинається з умови й завершується розв'язком, формуванням гіпотези, завершується суб'єктивним переконанням у можливості задовольнити умову і вимоги задачі, його призначення та є наслідком апробаційних дій.

 

2.1. Нестандартні уроки - як акцентуація розвитку творчих здібностей

Відомо, що будь-який урок – це складне педагогічне явище, витвір вчителя, на якому учні демонструють свої знання, уміння та навички. Іноді діти ідуть на урок із задоволенням, іноді без нього. Як зацікавитидітей? Як прикріпити їх увагу до свого предмету? Як донести матеріал до їх свідомості яскраво і красиво, щоб запам'яталась надовго і назавжди?

Іноді можна почути, що математика складана, суха і нецікава наука. Людей, які люблять математику, це вражає й ображає. Математика – красива й глибока, як чиста криниця. А завдання вчителя полягає в тому, щоб розкривати перед учнями її емоційній бік. Як краще цього домогтись? Красивими, цікавими уроками. Уроками, які пробуджують цікавість і працьовитість, фокусують увагуй зосередженість. Отже, нестандартні уроки. Вони не вкладаються в рамки виробленого і сформульованого дидактикою. На цьому уроці можна не дотримуватись чітких етапів навчального процесу, методів, традиційних видів роботи. Для такого уроку характерною є інформаційно-пізнавальна система навчання – оволодіння готовими знаннями, пошук нових форм викладу, розкриття внутрішньої сутності через гру, змагання або нетрадиційні форми роботи з дітьми, використовувати власні дидактичні матеріали, часто саморобні і тим більше корисні для учнів.

Для поліпшення розуміння, закріплення та відтворення інформації доцільно проводитись такі уроки як: урок-змагання, урок-вікторина, урок - круглий стіл, урок-гра та ін. Щоб зацікавленість учнів до вивчення математики не знижувалась, доречно систематично проводити ігри з використаннямінтерактивних технологій. Така організація учбової діяльності на уроці дає можливістьреалізувати принципи диференціації навчання, оскільки гарантує активізацію уваги учня на тому чи іншому етапі уроку. Так, учні з низьким рівнем навчальних здібностей можутьзабезпечити команді бали на І етапі уроку, а учні з високими здібностями–виступатиіз захистами творчих робіт. Другий етап уроку – поле діяльності для учнів з середніми навчальнимиздібностями.

Позакласна робота з математики дуже важлива для пробудження в учнів інтересу до математики. Томуматематичні вікторини, змагання, ігри, прес-конференції, вечори сприяютьпідвищенню математичної культури, розширюють і поглиблюють здобуті на уроках знання, показують застосування їх на практиці, розвиваються мислення, математичні здібності, допомагають ввійти у світ наукових і технічних ідей.

Підготовка до нестандартного уроку може здійснюватися за алгоритмом колективної творчої діяльності: формулювання мети уроку, планування, підготовка, проведення уроку, підсумковий аналіз. Нехтування елементами цієї структури зводить нанівець зусилля педагога. Доцільно розглянути стратегію, тактику організації колективної творчої діяльності учнів на кожному з етапів. Нестандартні уроки руйнують застиглі штампи в організації навчально-виховного процесу в школі, сприяють оптимальному розвиткуі вихованню учнів. Учнів стомлює одноманітність, нетворча робота. Фізіологи з'ясували, що в 90% школярів втомленість під годину навчальної діяльності виникаєне від нестачі енергії, а від її надлишку. Учні більше втомлюються на нецікавих уроках, ніж на уроках, наповнених цікавім змістом. Саме тому вчитель повинен уміло використовувати інтонаційні засоби мови, стежити за її гучністю та інтенсивністю, чергувати різноманітні методи навчання, використовувати гру, створюватиситуації зайнятості та емоційного переживання. Гігієна розумової праці пропонує вміле поєднання логічних міркувань з науковими образами, постійний перехід від простого матеріалу до складнішого, що забезпечує нормальне функціонування кори головного мозку, віддаляє прояви стомленості.

 

2.2. Роль і місце дидактичних ігор на уроках математики.

Дидактичні ігри на уроках математики можна використовувати дляознайомлення дітей з новим матеріалом та для його закріплення, дляповторення раніше набутих уявлень і понять, для повнішого і глибшого їхосмисленого засвоєння, формування обчислювальних, графічних умінь танавичок, розвитку основних прийомів мислення, розширення кругозору.

Систематичне використання ігор підвищує ефективність навчання.

Дидактичні ігри добираються відповідно до програми. В іграхматематичного змісту ставляться конкретні завдання. Так, якщо на уроціучні повинні ознайомитися з принципом утворенням будь-якого числа, то йдидактична гра підпорядковується цій меті, сприяючи розв’язуваннюпоставленого завдання.

У дидактичних іграх діти спостерігають, порівнюють, класифікують

предмети за певними ознаками, виконують аналіз й синтез, абстрагуютьсявід несуттєвих ознак, роблять узагальнення. Багато ігор вимагають уміннявисловлювати своє думку в зв’язній і зрозумілій формі, використовуючиматематичну термінологію.

Саме в іграх розпочинається невимушене спілкування дитини з колективомкласу, взаєморозуміння між учителем і учнем. У процесі гри в школяріввиробляється звичка зосереджуватися, працювати вдумливо, самостійно.Розвивається увага, пам’ять, жадоба до знань. Задовольняючи своюприродну невсипущу потребу в діяльності, в процесі гри дитина“добудовує” в уяві все, що недоступне їй у навколишній дійсності, взахопленні не помічає, що вчиться – пізнає нове, запам’ятовує,орієнтується в різних ситуаціях, поглиблює набутий раніше досвідпорівнює запас уявлень, понять, розвиває фантазію.

У грі найповніше проявляються індивідуальні особливості, інтелектуальніможливості, нахили, здібності дітей.Гра належить до традиційних і визнаних методів навчання і вихованнядошкільників, молодших школярів і підлітків.

Цінність цього методуполягає в тому, що в ігровій діяльності освітня, розвиваюча й виховніфункції діють у тісному взаємозв’язку. Гра як метод навчанняорганізовує, розвиває учнів, розширює їхні пізнавальні можливості,виховує особистість.

 

2.3. Проблемні задачі як засіб розвитку творчих здібностей учнів

У сучасних умовах проблемі творчості і творчих здібностей особистості приділяють увагу педагоги, соціологи, психологи. Психологи переконливо довели, що задатки творчої здібності властиві будь-якій людині, будь-якій дитині. Не менш важливим є висновок психолого-педагогічної науки про те, що творчі здібності необхідно розвивати з раннього віку. Якщо ж дитину з перших років не привчати до творчої діяльності, то втрати від цього важко буде виправити в наступні роки. Отже, розвитку творчих здібностей дітей слід приділяти увагу з раннього дитинства. Над проблемою розвитку творчих здібностей працювали багато науковців. Різні аспекти цього питання розглядалися у працях Л. Виготського, Г. Костюка, Т. Кудрявцева, Л.Леонтьева, А. Пономарьова, М. Левітова, В. Сидоренка.

Учені стверджують, що найбільш сприятливі умови для розвитку творчих здібностей створюються у процесі праці. Основна праця дітей – навчання. Цілком закономірно, що для виховання в учнів творчих рис їх навчання треба зробити творчим. На жаль, у наших школах переважає репродуктивне навчання. Цей процес часто являє собою передачу інформації від учителя до учнів. Учитель подає готові знання, а учні пасивно їх запам'ятовують, і чим точніше на наступних уроках вони відтворюють одержані в готовому вигляді знання, тим краще вони «встигають». Але репродуктивно набуті знання й уміння не знаходять застосування на практиці.

Процес навчання у школі має бути спрямований не тільки на набуття учнями певних знань та вмінь, а й на формування в них інтересу і здібностей до певної діяльності, зокрема навчальної. Учні мають постійно вчитися застосовувати на практиці свої знання і вміння.

Разом з теоретичними задачами вчитель повинен використовувати і практичні задачі, які можна виконати у матеріалі. Це, безумовно, правильно, оскільки практична перевірка теоретичного рішення забезпечує закріплення його у пам'яті, формує в учнів упевненість у важливості і необхідності теоретичних знань та своєї праці. Але, на жаль, використання творчих задач ще не набуло широкого застосування у практиці навчання. Інколи вчителі додатково пропонують учням, які раніше за інших виконали завдання, окремі вправи.

У формуванні знань і вмінь важливу роль відіграє систематичний контроль за діями і операціями учнів із зазначенням помилок і досягнень. Але успішність пошуку правильних засобів виконання тих чи інших дій залежить не тільки від зовнішнього контролю та оцінки, але й від самоконтролю. На засвоєння нових умінь великий вплив мають попередній досвід та знання. Чим більша в учня база попередніх знань та вмінь, тим швидше він оволодіє новими вміннями та пристосується до роботи в нових умовах, до вирішення нових творчих задач. Творчий характер задачі для учня залежить від його підготовки до розв'язання подібних задач. Тому одна і та ж задача для одного учня є творчою, а для іншого – ні. Більш того, для одного і того ж учня певна задача в різний час може мати різний рівень складності. Якщо учень не володіє необхідним мінімумом інформації або не може використати на практиці раніше засвоєну інформацію, то задача для нього стає не творчою, а просто непосильною. Задача не є творчою і в тому випадку, якщо учень добре володіє алгоритмом її розв'язання.

Для опанування раціонального способу розв'язання творчих задач важливе значення має послідовне виконання певних розумових дій. А для цього необхідно навчити школярів аналізувати задачу, чітко виділяти в ній дані, відомі та невідомі елементи і умови, розчленовувати процес розв'язання на окремі етапи з використанням відповідних алгоритмічних, напівевристичних, евристичних прийомів тощо. Приступаючи до розв'язання творчої задачі, учень повинен добре зрозуміти та наочно уявити її зміст, визначити її приналежність до одного з відомих класів задач.

Таким чином, для розвитку в учнів творчих здібностей учитель повинен максимально активізувати їх розумову діяльність. Як уже зазначалось, проблемні ситуації є одним з важливих засобів формування і розвитку творчих здібностей учнів. Для цього необхідно згадати раніше засвоєні та придбати нові знання та вміння, ліквідувати невідповідність між науковими та практичними знаннями й уміннями. Учитель використовує проблемні ситуації, для розв'язання яких учням необхідно застосовувати набуті знання та вміння в нових конкретних умовах. Цей методичний прийом дозволяє залучати до розв'язання проблеми весь клас. Тобто учням необхідно вибрати з набутої системи знань ті, які дозволять успішно вирішити поставлену задачу. Аналіз проблемної ситуації, використання раніше засвоєних та нових знань (довідкова література) дозволяє учням успішно розв'язувати проблемні задачі, а отже, розвивати їхні творчі здібності.

Отже, проблемне навчання сприяє  розвитку у школярів логічного мислення, вміння висловлювати власну думку, робити висновки та використовувати набуті знання у подальшому житті, дає змогу самовиразитися і само реалізуватися.

3. Формули скороченого множення, їх застосування у математиці

Деякі правила скороченого множення були відомі стародавнім китайським і грецьким математикам близько 4 тис. років тому. Тоді вони формулювали ці правила не за допомогою букв, а словами, і доводили геометрично (тільки для додатніх чисел). Наприклад, тотожність(a+b)²=a²+2ab+b² у другійкнизі «Начал » Евкліда (3 ст. до н.д) формулювалась так: « якщо пряма лінія (мається на увазі відрізок) як-небудь розсічена, то квадрат на всій прямій дорівнює квадратам на відрізках разом із двічі узятим прямокутником, що міститься між відрізками ».

Геометричний зміст тотожності наведений на малюнку.

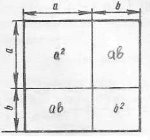
Йдеться про формулу квадрата суми, яку ми символічно записуємо так:

.

♦ Нестандартні уроки руйнують застиглі штампи в організації навчально-виховного процесу в школі, сприяють творчому розвиткуі вихованню учнів

♦Гра – як один з найважливіших засобів розвитку творчої особистості

Гра “Математичне лото ”

Кожна команда отримує набори карток. Відповіді називають. Кожне завдання–одне слово. Складають вислови про математику.

Картка 1. Розкласти многочлен на множники:                17а+17;               5а2-20аb.	Картка 2. Перетворити вираз у многочлен:                (a+7)2;               3x(x3-4x+6).
Картка 3.  Розв`язатирівняння:                4x2-12x=0;               x2-7x=0.	Картка 4. Розкласти многочлен на множники:                a2-9;               c4-m6.

 

Відповіді:

 

Картка 1.                                        17(a+1);                                        5a(a-4b).	Картка 2.                                        a2+14a+49;                                        3x4-12x2+18x.
Картка 3.                                        0; 3; b)  0; 7.	Картка 4.                            (a-3)(a+3);                           (c2-m3)(c2+m3).

 

Математика– яка	це наука, вимагає
найбільше Софія	фантазії. Ковалевська.

 

 

Гра«Шифрувальник»

Заповнити порожні клітинки таким одночленом, щоб утворилась правильна тотожність.

a) ²-y²=(a-)(a+);  (У)                        в) (5m-)(5m+)=25m²-16a²;  (Г)

b) (x+)²=²+2y+y²;  (Р)                      г) (4a-)(+5x²)=16a²-25x⁴.  (Д)

Гра“Знайдипомилку”

 Знайти помилку і записати вирази правильно:

1.                (x-7)²=x²-14x+40;
2.               (x-7)²=x²-7x+49;
3.                (x+4)²=x²+4x+16;
4.               (y²-4)(y²+4)=y²-16.

 

Гра «Кодованівправи»

Біля правильної відповіді поставити порядковий номер умови

Умова	Відповіді
1. (1 - ав)2 =	=   п2 + 4ап + 4а2           6.
2. х2 – 16 =	= (х + 2)(х2 – 2х + 4)    4.
3. 9m2 – 4х2 =	= (4 - а)(16 + 4а + а2)    5.
4. х3 + 8 =	= (х - 4)(х + 4)               2.
5. 64 – а3 =	= (3m – 2х)(3m + 2х)    3.
6. (п2 +2а)2 =	= 1 – 2ав + а2в2             1.

 

Гра«Кубик-екзаменатор»

У руках вчителя великий кубик, на гранях якого записи: а² - b², а² +2аb + b², а² - 2аЬ + b², а³ + b³, а³ - b³.

Учитель показує учням кожну з цих граней і пропонує розкласти многочлени на множники, а розклад записати в зошит. Потім учні обмінюються зошитами й перевіряють відповіді за записами на решті граней.

«Рухливі вправи»

Станьте біля парти, слідкуйте за осанкою, дивіться на слайд.

Якщо відповідь правильна, хлопніть два рази в долоні.

Якщо відповідь хибна, підніміть високо руки догори.

•                 х² - 36 = (х + 6)(х – 6)
•                 (х + 3)² = х + 9
•                 (у – 9)(у + 9) = у² –  9 
•                 (а² – 2аb + b²) = (a – b)²

 

Гра «Сніжинка - твій новорічний оберіг» 

 (Актуалізація опорних знань)Напередодні новорічних свят всі прикрашають ялиночку. Ми сьогодні будемо прикрашати ялиночку вашими знаннями. Адже знання - справжня прикраса

1.              
2.              
3.              
4.              
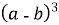
5.               Які доданки називаються подібними?
6.               Як відкрити дужки, перед якими стоїть знак «+»?
7.               Як відкрити дужки, перед якими стоїть знак «-»?
8.               Як розкрити дужки, перед якими нема ніякого знака?
9.               Означення многочлена.
10.                    Як помножити одночлен на многочлен?
11.                    Як помножити многочлен на многочлен?

За правильну відповідь дитина отримує оберіг - сніжинку

Гра “Естафета”

Допишіть формули скороченого множення.

На дошці написано завдання для кожної команди. Діти по черзі підходять до дошки і дописують праву частину формули. Конкурс оцінюється до чотирьох балів.

Пропоную учням виправити помилки, допущені командою суперників. Береться  до уваги правильність виконання завдання та швидкість.

 

♦ Проблемні (нестандартні) задачі

1. Розв’язати рівняння:    (х+1)⁴  +(х+5)⁴=32

Розв’язок:   заміна у=х+3, тоді

(у-2)⁴+(у+2)⁴=32,

((у²+4)-4у)²+((у²+4)+4у)²=32,

2(у²+4)²+2·16у²-32=0,

у⁴+24у²=0,

у=0. Отже, х+3=0, звідси х=-3.

Відповідь: х=-3

2.  Обчислитиsin³λ-cos³λ, якщоsinλ-cosλ=а.

Розв’язок: sin³λ-cos³λ=(sinλ-cosλ)(sin²λ+sinλcosλ+cos²λ)=а(1+sinλcosλ).

sinλ-cosλ=а , звідсиsinλcosλ=(1-а²)/2.

Тоді: sin³λ-cos³λ= а(1+(1-а²)/2=а(3-а²)/2.

Відповідь: а(3-а²)/2.

 

 

Висновки

 

Природа щедро наділила кожну здорову дитину можливостями розвиватися, і потрібно лише знайти, як реалізувати ці можливості, і тоді кожна здорова дитина зможе піднятися на найбільші висоти творчої діяльності. Творчість – доля всіх в тому чи іншому ступені, вона ж є нормальним та постійним супутником дитячого розвитку. Для розвитку учня дуже важливим є формування багатьох інтересів. Слід зазначити, що для школяра взагалі характерно пізнавальне ставлення до світу. Така цікава спрямованість має об'єктивну доцільність. Інтерес до всього розширює життєвий досвід дитини, знайомить його з різними видами діяльності, активізує його різні здібності.

Життя вчителя – це обов'язок бути світочем, утверджувати ідеали правди, краси, добра. Учитель - це той, хто сіє добре зерно. Щастя для нього - гідні учні, які сяють, як сонце, наслідуючи його чесноти та продовжуючи його доброчинність.

А для цього необхідно перетворити кожний урок у школі в урок мислення-спілкування, де істина зароджується у палкій суперечці, у діалозі, під час якого важливо навчи­ти кожного учня міркувати, знаходити нові, оригінальні рішення і отримувати задоволення від навчання.

Навіть разове переживання успіху може докорінно змінити психологічне самопочуття учня. Адже успіх — спусковий механізм подальшого творчого руху особистості. Творча діяльність, є більш складною за своєю сутністю, доступна тільки людині. Є велика "формула", яка підіймає завісу над таємницею народження творчого розуму: "Спочатку відкрити істину, відому багатьом, потім відкрити істини, відомі деяким, і нарешті відкрити істини, нікому ще невідомі". Мабуть, це і є шлях становлення творчої сторони інтелекту, шлях розвитку  таланта. Наш обов'язок - допомогти дитині стати на цей шлях.

Творчі здібності, як і інші здібності людини, вимагають постійного тренування. Завдання вчителя – збудити здібності своїх учнів, виховувати в них сміливість думки і впевненість у тому, що вони розв’яжуть кожну задачу, у тому числі і творчого характеру.

Таким чином, організація навчально виховного процесу з метою розвитку творчих  здібностей та пізнавальної активності учнів передбачає планування роботи за такими основними напрямами:

1) докорінне змінення позиції учнів у процесі навчання, підвищення їхньої ролі, розширення функцій. Мається на увазі гуманізація навчально виховного процесу, що принципово змінює не тільки ставлення учнів до навчальної діяльності, а й до всього, що відбувається на уроці.

2) організація співтворчої діяльності на уроці.

3) створення сприятливих умов для учнів з різними навчальними здібностями шляхом диференціації, особистісно орієнтованого підходу, щоб кожен учень працював на максимальній длянього межі можливостей.

Отже, потрібно не формальне, а творче, розумне засвоєння і застосування педагогічного досвіду.

 

 

 

 

 

 

 

 

Список використаної літератури

1.               Галатюк Ю.М. Теоретичні й методичні аспекти формування інтелектуальних умінь у контексті навчально-пізнавальної діяльності / Ю.М.Галатюк // Оновлення змісту, форм та методів навчання і виховання в закладах освіти: Збірник наукових праць. Випуск 40. – Рівне: РДГУ, 2009. – С.78 – 84.
2.               Колінець Г.Г. Формування дослідницьких здібностей у старшокласніків// обдарованих дитина. - 1999. - № 5. - С. 10-13.
3.               Моляко В.А. Творчаобдарованість і виховання творчої особистості. - К., 1991.
4.               Монько О. Плекаємо творчого учня/О. Монько// Математика [газета]. - 2008. - Квітень (№ 14). - С.1-7.
5.               Орос В.М., Петечук В.М., Петечук К.М. Контрольно-практичні роботи з  математики. Частина І. – Ужгород: Інформаційно-видавничий центр ЗІППО, 2016 – 200с.
6.               Петечук В.М., Сігетій І.П. Завдання та розв’язки районних і міських олімпіад з математики 2000 – 2006 років. – Ужгород: Інформаційно-видавничий центр ЗІППО.- 2007 – 208с.
7.               Станіславська Г.П. Розвиток творчих здібностей школярів. - Тернопіль: Навчальна книга - Богдан, 2007. - 64 с.
8.               Сучасні технології формування логіко-математичної компетентності в дітей дошкільного та молодшого шкільного віку / за заг. ред. Н.П. Тарнавської., Н. Ю. Рудницької, Ю. М. Мурашевич – Житомир: ФОП «Левковець», 2015. – 430 с.
9.               Теплицький І. О. Розвиток творчих здібностей школярів засобами комп’ютерного моделювання: психолого-педагогічний аспект / Теплицький І. О., Семеріков С. О. // Актуальні проблеми психології: Психологічна теорія і технологія навчання / За ред. С. Д. Максименка, М. Л. Смульсон. – К. : Міленіум, 2015. – Т. 8, вип. 1. – С. 225–232.