ТВОРЧЕ ВИКОРИСТАННЯ ПРОГРЕСИВНИХ ТЕХНОЛОГІЙ ТА ВПРОВАДЖЕННЯ ПРИНЦИПІВ ОСОБИСТІСНО-ОРІЄНТОВАНОГО НАВЧАННЯ ВЧИТЕЛЯМИ ПРИРОДНИЧО-МАТЕМАТИЧНОГО ЦИКЛУ З МЕТОЮ РОЗВИТКУ ЖИТТЄВИХ КОМПЕТЕН

Кормілець Тетяна Борисівна,

вчителі математики КУ ССШ №17

ТВОРЧЕ ВИКОРИСТАННЯ ПРОГРЕСИВНИХ ТЕХНОЛОГІЙ ТА ВПРОВАДЖЕННЯ ПРИНЦИПІВ ОСОБИСТІСНО-ОРІЄНТОВАНОГО НАВЧАННЯ ВЧИТЕЛЯМИ ПРИРОДНИЧО-МАТЕМАТИЧНОГО ЦИКЛУ З МЕТОЮ РОЗВИТКУ ЖИТТЄВИХ КОМПЕТЕНЦІЙ УЧНІВ

Актуальність проблеми полягає в тому, що проблеми сучасної освіти призвели до того, що вперше на початку 70-х років ЮНЕСКО віднесло проблему реформування освіти до розряду глобальних проблем людства. Більшість дослідників згідні з твердженням відомого американського соціолога Д. Белла, що провідною нацією буде та , яка створить ефективну систему освіти, щоб максимально розвинути потенціал своїх молодих співвітчизників. Звідси необхідність впроваджувати та удосконалювати нові технології навчання, що орієнтовані на повну реалізацію творчих сил учнів, які відкидають провідну роль вчителя на уроці, що дають можливість розкрити індивідуальність кожної дитини, допомогти їм у розвитку і виробленні впевненості у собі, надати можливість проявити і утвердити себе.

Одна з основних таких технологій – це особистісно-зорієнтоване навчання, мета якого полягає у створенні оптимальних умов для розвитку і становленні особистості як суб'єкта діяльності і суспільних відносин та формування на цій основі життєво-необхідних компетенцій учнів.

Дуже часто під особистісно-орієнтованим уроком розуміють гуманне, шанобливе ставлення до учня, щоб створити позитивний емоційний настрій класу на роботу. Буває, вчитель не виставляє низької оцінки, намагається допомогти слабким учням, широко використовує нестандартні уроки, насичені творчими завданнями. Все це, безумовно, робить урок цікавішим, але його ще не можна вважати особистісно-орієнтованим. Суть останнього – не просто створення доброзичливої творчої атмосфери, а постійне звернення до суб'єктивного досвіду учнів, тобто досвіду їхньої життєдіяльності.

І найважливіше – визнання самобутності та унікальності кожного учня. Основний задум особистісно-орієнтованого уроку в тому, щоб розкрити зміст індивідуального досвіду учнів, порівняти його з набутим.

Під час організації особистісно-орієнтованого уроку професійна позиція вчителя полягає в тому, щоб знати і з повагою ставитися до будь-якого висловлювання учня за темою. В цих умовах учні прагнутимуть висловлювати свої думки, пропонувати свої варіанти, не боятимуться помислити.

Для того, щоб будь-яка людина, залучена до певної діяльності виступала в ній як суб'єкт, перш за все, вона має усвідомлювати особистісно значиму мету цієї діяльності. З цього виходить, що якщо ми хочемо включити особистість в освітній процес (той же урок), вона повинна бачити в ньому певну значимість. Звідси наступна теза: робота вчителя без мотивації і особистісних підстав учнів, рівнозначна роботі в порожньому класі.

Зупинимось на основних «вузлах» технології особистісно-зорієнтованого уроку.

1. Етап орієнтації.

Будь-яка діяльність, у тому числі і освітня, це своєрідний рух певним «шляхом». І для того, щоб цей рух був успішним, крім мети учневі треба знати також «етапи шляху», – коли, протягом якого часу вивчатиметься тема, коли контрольна, консультація, залік чи інша форма роботи. Окрім усного повідомлення етапів вивчення теми, кількості відведених годин, днів-консультацій, варто практикувати на початку теми роздачу індивідуальних карток, де передбачені завдання, задачі, які учень повинен вміти розв'язувати в результаті вивчення теми, дати проведення залікових робіт, контрольних робіт. Це дає можливість дитині вдома працювати індивідуально над завданнями, готуватись самостійно до контрольної чи залікової роботи, вибирати і розв'язувати із запропонованого переліку ті завдання, які вже вивчено на даний час на уроках, тобто планувати свою діяльність під час вивчення теми. З об'єкта навчання дитина перетворюється на суб'єкта цілеспрямованої діяльності.

Можна висвітлювати завдання, які діти повинні уміти розв'язувати в результаті вивчення теми на стенді «Вивчаємо тему». Такі стенди в кабінетах математики часто використовується для забезпечення усвідомлення учнями кінцевої мети, і, як подача довідкової інформації з теми (формул, означень і т.д.).

2. Етап досягнення цілі.

Тему уроку, його мету, план доводять до відома учнів одразу ж після сигнального дзвінка словесно і наочно. Вчитель чітко й переконливо інформує учнів відносно того, що й навіщо вони робитимуть на даному уроці. В цьому вступному інструктажі його пізнавальна привабливість – матеріал пов'язаний з певною цікавою значною проблемою, визначено проблемні запитання.

Важливо пояснити учням значення матеріалу, що вивчається, для практичної діяльності, для пізнання інших наук, для побудови цілісної системи знань із даного предмета, які будуть потрібні під час заліку. Ось декілька засобів для більшого зацікавлення матеріалом, який вивчається:

1) Приваблива мета – перед учнем постає проста, зрозуміла і приваблива мета, яка стає для нього особистісно-вагомою метою, і він залучається до запланованої вчителем навчальної діяльності. Наприклад, при вивченні теми «Площі фігур» (5-й кл.), поставивши мету сформувати вміння в учнів знаходити площі прямокутників, фігур, що є комбінаціями прямокутників, площі поверхонь прямокутних паралелепіпедів, вчитель пропонує зіграти випадок «майстру з ремонту квартир необхідно скласти кошторис на витрати для ремонтних робіт (врахувавши витрати фарби на 1м2 і т. д.)»

2) Подив – учитель знаходить таку точку зору на навчальний матеріал, за якого навіть повсякденне стає дивовижним. Наприклад, учитель під час вивчення теми «Натуральні числа» запитує: «Діти, назвіть найбільше натуральне число!» Діти після деякого обмірковування з подивом виявляють, що такого числа не існує.

3) Відстрочена відповідь – на початку уроку вчитель ставить проблемне запитання, правильну відповідь на яке учень зможе сформулювати, отримуючи інформацію під час уроку. Наприклад, під час вивчення теми «Існування площини, яка проходить через три точки» учитель запитує: «Як визначити за допомогою звичайного шнура, чи буде стілець з чотирма ніжками стійкий?», «Чому стіл з трьома ніжками завжди стійкий?»

4) Помилка в поясненні – пояснюючи матеріал, учитель навмисно припускається помилки. При цьому учитель доводить до відома учнів свій намір. Наприклад, поставивши ціль – навчити дітей розв'язувати рівняння з відшуканням ОДЗ, вчитель пропонує рівняння 2х-(1/(х+2))+4=2(х+2)-(1/(х+2)) і стверджує, що розв'язком його є будь-яке число, методом такого розв'язування: 2х+4=2(х+2), 0х=0. Завдання дітей знайти помилку.

5) Практичність теорії – вступ до теорії вчитель здійснює через практичне завдання, вирішення якого корисне для учнів. Наприклад, на початку вивчення теми «Перпендикулярність прямої і площини» обговорюється проблема: «Як на практиці за допомогою мотузки й гирьки перевірити вертикальність виставлення стовпа. На чому повинна ґрунтуватись така перевірка?»

Використовуючи такі постановки мети, вчитель розвиває пізнавальний інтерес будь-кого з учнів, вони усвідомлюють необхідність вивчення теми, бо вона буде потрібна у повсякденному житті.

3. Етап організації виконання плану діяльності. Ключову роль в особистісно-зорієнтованій діяльності відіграє надання учневі можливості вибору для нього як суб'єкта діяльності певних способів просування до визначеної мети, тих, яким він надає найбільшу перевагу. Це може бути варіант відповіді домашнього завдання, або вибір варіанта підготовки конспекту чи розв’язання завдань на закріплення – що завгодно, що, не порушуючи ходу пізнання, дозволяє учневі усвідомлювати процес суб'єктивного вибору. Наприклад, одна справа викликати трьох учнів і запропонувати їм відповідне завдання і, зовсім інша, – назвати імена учнів і запропонувати їм самим вибрати варіант роботи.

Цікавою формою роботи для дітей є така самостійна робота, під час якої можна не тільки вибирати завдання, але й порухатися під час уроку. На пронумерованих столах є завдання. Учні на вибір підходять до стола із завданнями і пробують його розв'язати. У випадку виникнення труднощів переходять до іншого стола або просять допомоги у вчителя. Така форма роботи дає можливість без стресу провести дитині самооцінку (чого я ще не навчився ), немає психологічного тиску, обмежень у часі, є можливість вільно рухатись (тут розвиток рухового апарату). Таку роботу варто проводити і в старших класах, де дуже рідко ми приділяємо увагу фізкультхвилинці.

Завдання вчителя допомагати розвитку дитини. Здійснюючи це завдання, учитель, спираючись у своїх педагогічних діях на закони розвитку, підтримує їх, співпрацює з ними, а не творить дитину подібну на себе. Він повинен не стільки вчити дитину, скільки направляти дитину. Так під-час уроку – корекції знань і умінь, учні виконують самостійну роботу. Тут відбувається самостійне подолання труднощів і виправлення помилок, що є рушійною силою розвитку. Тому допомога і підтримка вчителя надається лише тоді, коли це насправді потрібно і згідно з девізом «допоможи мені зробити це самому». Слід відзначити, що тут допомога містить індивідуальний характер.

Присутність учителя мають відчути ті учні, які потребують допомоги, мають певні труднощі з вибором шляху до розв'язання завдань та зосередження над ним. Вчитель є «невидимим» для тих, хто самостійно працює і успішно розв’язує завдання.

Ніхто не заперечує диференційований підхід, але слід його здійснювати безболісно, надаючи можливість слабкому учневі зробити завдання на вибір, не акцентувати увагу на завданнях, які дає вчитель для сильнішого і слабкого учня (зробіть це мовчки).

Розглянемо ще один із «секретів» особистісно-зорієнтованого навчання: це зворотній зв’язок педагога і учня. Ось деякі з методів і заходів психолого-педагогічної підтримки діяльності учнів: заохочення, створення яскравих наочно-образних уявлень, навчально-пізнавальна гра, створення ситуації успіху, пізнавальний інтерес, створення проблемної ситуації, спонука до пошуку альтернативних вирішень, виконання творчих завдань, кооперація учнів, створення ситуацій взаємодопомоги. Варто в процесі уроку використовувати усну оцінку «Молодець», «Добре», словесну підтримку «Нехай буде, нічого страшного», «Добре, а може ще будуть якісь думки», «Слушне зауваження» та інші.

Проте надалі потрібно виключати із бесіди з учнями таких навіть поодинокі вислови як, «Ні, не добре», «Якщо я ще одну помилку знайду, поставлю одиницю», при запитанні учня «Можна?», не дослухавши запитання, давати відповідь: «Ні, не можна!». Утримуватися від поспішних оцінок, наприклад, при розв'язуванні дитиною задачі, при затрудненні виконання простої арифметичної дії ставити 1 бал. Необхідно постійно вислуховувати думку учня, не нав'язувати власних способів розв'язування. На перший погляд це дрібниці, які ми інколи не помічаємо, але потрібно дивитися на речі очима дитини, ставити себе на уроці в роль учня.

4. Етап контрольно-оцінювальний. Залучення учнів до контролю за ходом навчальної діяльності (парні, групові форми взаємоконтролю, самоконтроль).

Участь учнів у виправленні зроблених помилок, неточностей, осмислюванні їх причин (взаємо- і самоаналіз).

Надання учням можливості самостійно або за допомогою вчителя, інших учнів порівнювати оптимальний результат із критеріями еталона (мети).

Використання механізмів «цінування» (позитивного ставлення до успіху школяра) та «оцінювання» (виставлення оцінок, поурочного балу, рейтингових оцінок) не тільки кінцевого результату, а й процесу навчання.

5. Заключний етап – усвідомлення ситуації досягнення мети, переживання ситуації успіху, закріплення позитивної мотивації стосовно діяльності- еалізація механізму «цінування».

Механізм «цінування» – це вираження педагогом свого позитивного ставлення, задоволення з приводу діяльності учнів і їх результатів. Необхідно відрізняти «цінування» від «оцінювання».

Оцінювання передбачає кількісну та якісну (як позитивну так і негативну) оцінку навчальної праці школярів. «Цінування» може бути тільки позитивним, воно передбачає автентичність педагога – відповідність почуттів, які він виявляє, тим почуттям, які реально переживає. Саме «цінування» є основним механізмом культивування системи гуманістичних, соціально-орієнтованих цінностей учнів.

Цікава математика: ідеї яскравих ілюстрацій сухої теорії

Коли школярі з легкістю опанують множення, у середніх або старших класах можна їх познайомити з альтернативними ментальними методами, вивчення яких не передбачено програмою.

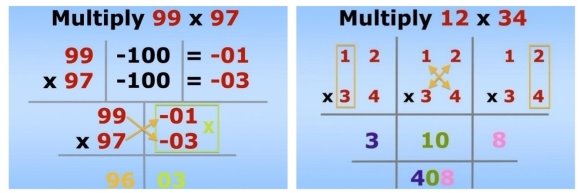
Альтернативні методи множення двозначних чисел

Вирахувати значення логарифми та знайти корені від числа можна швидше, коли сформувалось уявлення закономірністі цих обчислень. При чому спеціалісти стверджують, що графічно оформлену інформацію мозок людини сприймає швидше за числову.

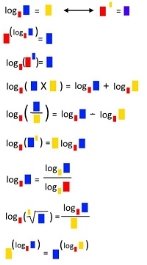
Приклади графічного зображення формул обчислення логарифмів

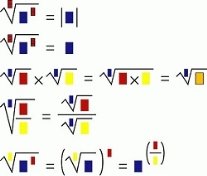
Приклади графічного зображення формул знаходження кореня від числа

В уяві більшості школярів алгебраїчні приклади так і залишаються просто числами. І якщо спитати, яке візуальне підґрунтя у такого типу алгебраїчних  вправ, впевнені, меншість надасть правильну відповідь.

Запропонуйте школярам візуалізувати алгебраїчні приклади за допомогою звичайних математичних закономірностей!

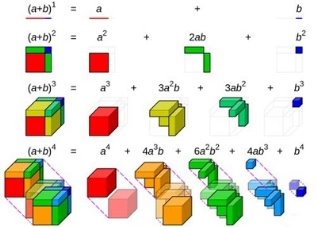
Приклад візуалізації алгебраїчних вправ

Провівши опитування знайомих, спостерігається закономірність: більшість з опитаних, цікавлячись в школі математикою, цілковито не розуміла сенс тригонометрії. Синуси, косинуси, тангенси, складні формули їх обчислення – все це так і залишилося теорією, яка незрозуміло звідкіля і для чого бралась. Може, якби пояснення тригонометричних дій супроводжувалось таким графічним відтворенням сухої теорії, зміст сприймався би жвавіше:

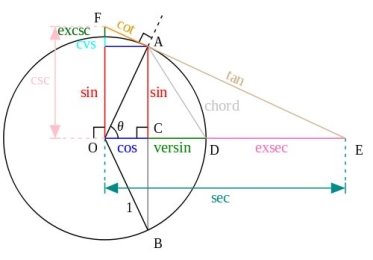
Графічний зміст основних тригонометричних понять

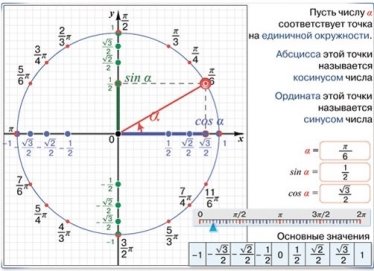
Схема обчислення синусів і косинусів

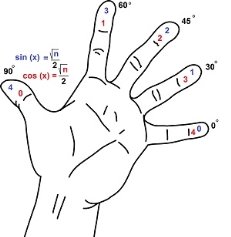
Підказка обчислення синусів та косинусів, яка завжди при собі

Графіки функцій мають математично обґрунтовану закономірність побудови. Поясніть учням сенс теорії, а для швидкого її запам’ятовування, покажіть їм веселих чоловічків, рух рук яких візуалізує графіки певних функцій.

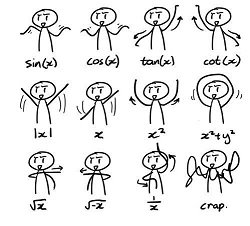
Динамічні графіки функцій

Під час практичних занять в якості творчого, запропонуйте учням завдання, на кшталт:

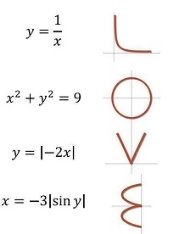
Сучасні освітні технологіїна уроках математики

• E-learning (цифрова освіта) Електронне навчання (Е-навчання) - це система навчання за допомогою інформаційних та електронних технологій.
• Навчання off-line. Оффлайн-навчання – це метод отримання нових знань в аудиторії під час безпосереднього спілкування викладача та учня.
• Навчання оn-line. Онлайн-навчання – це метод отримання нових знань за допомогою Інтернету в режимі реального часу. Комунікація між учасниками процесу відбувається за допомогою комп'ютера.
• Змішане навчання (blended learning). Змішане навчання – це методика формальної освіти, згідно з якою учень засвоює одну частину матеріалу онлайн, частково самостійно керуючи своїм часом, місцем, шляхом і темпом навчання, а іншу частину матеріалу вивчає у класі.
• Перевернуте навчання – це метод навчання, при якому вся теоретична і лекційна програма вивчається вдома, а в класі з учителем детально розбираються завдання і вправи по темі.
• Адаптивне навчання – це навчальна модель, яка використовує техніку і нові технології для потреб учнів в якості «інтерактивних навчальних пристроїв».

Звісно, навчання в школі – це двостороння взаємодія між учителем і учнем. Тому успіх залежить від докладених зусиль обома сторонами! А ось чи буде учень сприймати математику, як суху теорію чи справді закохається у предмет і запам'ятає уроки на все життя – цілковито залежить від вчителя!

Список використаних джерел

1. Хмель В. П. Упровадження інноваційних технологій у вивчення циклу математичних дисциплін  -  [ Електронний ресурс ] – Режим доступу: http://archive.nbuv.gov.ua/portal/Soc_Gum/Vlush/Ped/2011_13_2/13.pdf
2. Примакова В.В. Інноваційні технології навчання в сучасній початковій школі - [Електронний ресурс] – Режим доступу: http://archive.nbuv.gov.ua/portal/Soc_Gum/Tvo/2011_4/003.pdf
3. Ю.В. Триус «Інноваційні інформаційні технології у навчанні математичних дисциплін» - [ Електронний ресурс ] – Режим доступу: http://ena.lp.edu.ua:8080/bitstream/ntb/15095/1/15-Tryus-76-81.pdf
4. Годованюк Т. Л. Метод навчальних проектів в курсі методики навчання математики  [Електронний ресурс] – Режим доступу: http://archive.nbuv.gov.ua/portal/soc_gum/pednauk/2010_2/295.pdf
5. Хмель В. П. Упровадження інноваційних технологій у вивчення циклу математичних дисциплін  [ Електронний ресурс ] – Режим доступу: http://archive.nbuv.gov.ua/portal/Soc_Gum/Vlush/Ped/2011_13_2/13.pdf
6. https://naurok.com.ua/post/7-matematichnih-tryukiv-poza-shkilnoyu-programoyu