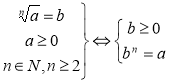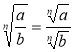Унаочнення до теми "Степенева функція"
Унаочнення до вивчення теми «Степенева функція»
Квадратні корені | |
| Означення квадратного кореня з числа а: | Означення арифметичного квадратного кореня з числа а: |
| число, квадрат якого дорівнює а. | |
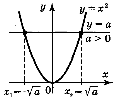
| Корінь рівняння: х2 = а. | Тотожності= а, а > 0. = | a |, a R. Основні властивості |
Унаочнення до вивчення теми «Степенева функція»
Квадратні корені
|
|
|
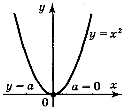
Означення квадратного кореня з числа а:
|
Означення арифметичного квадратного кореня з числа а:
|
|
число, квадрат якого дорівнює а. |
|
|
Корінь рівняння: х2 = а.
|
Тотожності
Основні властивості
|
|
Корінь n-гo степеня |
|
|
Означення кореня n-го степеня з числа а: число, n -й степінь якого дорівнює а. Корінь рівняння: х2 = а |
Означення арифметичного кореня n-го степеня з числа а:
|
|
|
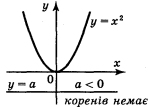
Якщо а < 0, то
Тотожності
Якщо
Основні властивості
|
Функція у = хp
|
|
p |
Графік |
D(y) |
E(y) |
Парність (непарність) |
Зростання (спадання) |
|
1
|
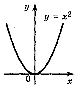
2
|
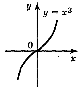
3
|
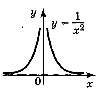
4
|
5
|
6
|
7
|
|
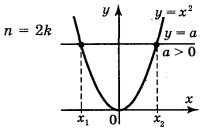
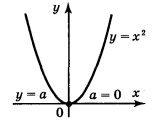
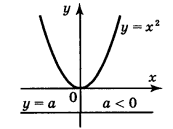
1. |
p=2k,
k
|
|
R |
[0; + |
парна |
спадає, якщо
х
якщо х |
|
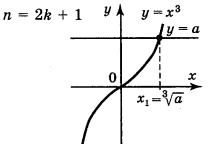
2. |
p=2k+1
k |
|
R |
R |
непарна |
зростає |
|
3. |
p=-(2k),
k |
|
x ≠ 0 |
(0; + |
парна |
зростає, якщо
х
якщо х |
|
4.
|
p=-(2k-1)
k |
|
x ≠ 0 |
y ≠ 0 |
непарна |
спадає
на проміжках (-
(0; + |
|
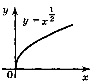
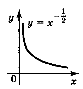
5. |
p > 0, p – не ціле, 0<р<1 |
|
[0;+ |
[0;+ |
ні парна, ні непарна |
зростає |
|
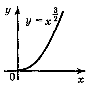
6. |
Р>0, p – не ціле, р > 1 |
|
[0;+ |
[0;+ |
ні парна, ні непарна |
зростає |
|
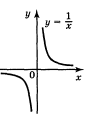
7. |
р < 0, р – не ціле |
|
(0;+ |
(0;+ |
ні парна, ні непарна |
спадає |


про публікацію авторської розробки
Додати розробку