Обобщающий урок по теме: "Показательные функции, уравнения, неравенства"

Цель урока:  обобщить и закрепить теоретические знания методов,  умения и навыки решения показательных уравнений и неравенств на основе свойств показательной функции; развивать умение наблюдать, обобщать, анализировать математические ситуации; воспитывать такие качества личности, как познавательная активность, самостоятельность, упорство в достижении цели, заинтересовать учеников в решении показательных уравнений неравенств для подготовки к ЗНО, побуждать учеников к самоконтролю, взаимоконтролю, самоанализу своей деятельности, получить опыт совместной деятельности, ощущение своего вклада в общее дело.

Ход урока

1. Мотивационно-ориентировочная часть

          С древних времен на Руси, прощаясь и встречаясь, говорили «Будь здоров». Сейчас мы говорим «Здравствуйте», т.е. люди желают здоровья друг другу. Здравствуйте ребята!

    Урок я хочу начать притчей “Однажды молодой человек пришел к мудрецу. Каждый день по пять раз я произношу фразу: «Я принимаю радость в мою жизнь» Но радости в моей жизни нет. Мудрец положил перед собой ложку, свечу и кружку и попросил «Назови, что ты выбираешь из них». «Ложку», - ответил юноша. Произнеси это 5 раз.».  «Я выбираю ложку», послушно произнес юноша 5 раз..  «Вот видишь, -сказал мудрец, повторяй хоть миллион раз в день, она не станет твоей. Надо…»Что же надо? Надо протянуть руку и взять ложку. Вот и вам сегодня надо взять свои знания и применить их на практике.

Давайте запишем число и классная работа. Запишите в тетрадях тему урока  "Показательные функции, уравнения, неравенства"

Именно поэтому Девиз нашего  урока: Достижения крупные  людям никогда не давались легко!

Ребята, наш урок-урок обобщения изученного материала .

Сегодня мы закрепим   и систематизируем знания   и умения, полученные на предыдущих уроках по этой теме, вспомним определения и формулы, виды и алгоритмы решения показательных  уравнений и неравенств. В  конце урока подведём итоги своей работы. Желаю вам  быть активными, внимательными и объективными!

Первым делом мы с вами пройдем тестирование проверку домашнего задания. Выполним тесты по вариантам.

Поменяйтесь тетрадями с соседом, проведем взаимопроверку. За каждое правильное задание 1 балл.

У каждого из вас есть оценочный лист. Возьмите и внимательно рассмотрите их. На листе оценивания написаны все виды работ, которые будут сегодня на уроке. А также максимальное количество баллов, которое вы сможете за это задание получить.  Подпишите его и там где тесты поставьте себе количество баллов, которые вы набрали. Максимум можете набрать 10 баллов.

Прежде чем приступить к практике по решению  уравнений и неравенств, нам нужно повторить все что вы знаете. Проведем Блиц – опрос. За каждый правильный ответ вы ставить 1 б

1.Какая функция называется показательной? (Функция заданная формулой у= а^х, где а>0 и  a≠1 называется показательной

2.Какова область определения функции y=0,3^x? (любое число)

3.При каком условии показательная функция является возрастающей? (а>1+)

4.При каком условии показательная функция является убывающей? 0<а<1

5.Определить при каком значении a функция проходит через точку А(1; 2)   а=2

6.

7.

8.

9. Приведите соответствие:

Самопроверка:  1-Б, 2-Д, 3-В, 4-А, 5-Е, 6-Г.

10. Назовите основные методы решения показательных уравнений: Функционально-графический метод, Метод приведения к одному основанию, Метод вынесение общего множителя за скобки, Метод введения новой переменной

11. Указать способы решения показательных уравнений.

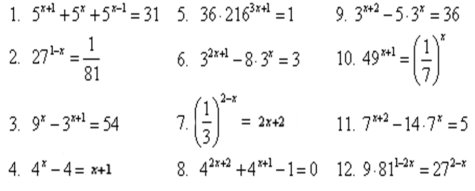
Диагностика уровня формирования  практических навыков

12. В чем отличие и сходство при решении показательных уравнений и неравенств? Сходство - Методы решения показательных неравенств аналогичны методам решения показательных уравнений.

Отличие: если функция возрастающая знак у неравенства сохраняется, если функция бывающая знак меняется

  М.В.Ломоносов говорил «Теория без практики мертва и бесплодна, практика без теории невозможна и пагубна. Для теории нужны знания, для практики сверх того , и умения»

И вот теперь вы должны проявить свои умения при решении различных показательных уравнений.

Давайте откроем учебник и решим № 117 ст. 29

Как мы можем назвать задачу? Прикладная задача - задача, решение которой имеет практическое значение (т. е. его можно реально применить для чего-либо).  (3б)

На сегодняшний момент важным для вас является сдача ЗНО. Поэтому предлагаю решить  несколько заданий из сборника для подготовки к ЗНО.

№1. Решите уравнение: = х + 3      

№2.  Указать наименьшее положительное решения неравенства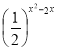

Древнегреческий поэт Нивей утверждал, что математику нельзя изучать, наблюдая, как это делает сосед. Поэтому будем сейчас работать самостоятельно

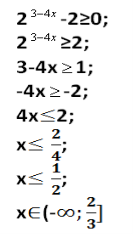
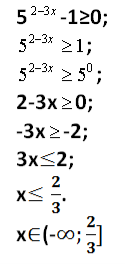
4^2х+1-6·2^2х+1<8;

2^2(2х+1) -6·2^2х+1-8<0;

Вводим замену: 2^2х+1=t;

t²-6t+8=0;

t₁=4;   t₂=2;

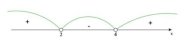
Получаем: 2<2^2х+1<4;

                    2¹<2^2х+1<2²;

                    1<2х+1<2;

                    0<2х<1;

                    0<х<0,5.

     Ответ: (0;0,5)

+8<9·;

+8<0;

Вводим замену: =t;

t²-9t+8=0;

t₁=8;   t₂=1;

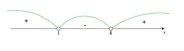
Получаем: 1<<8;

                    2⁰<<2³;

                    0<<3;

                    0<х-2<9;

                    2<х<11.

Ответ: (2; 11)

Посмотрите на презентации, давайте сделаем самопроверку. Максимум можете набрать 4 б

Что на свете всех милее, всех прекрасней и нужнее? Ответ: здоровье.  Чтобы сохранить свое здоровье давайте проведем физкультминутку минуту релаксации. Попрошу всех встать

Друзья! Давайте представим, что у нас выросли крылья! Мы можем летать. Как бы мы это сделаем? – Мы подвигаемся, поиграем в полёт!»

У меня есть крылья за спиной (руки - за спину)
Я летать умею над землёй. (руки – вверх)
Я взмываю ввысь и мир - Эгей! (руки – высоко вверх, делаем взмахи)
На ладошке умещается моей.

Пальчики как перышки расправлю, (встряхиваем кисти рук)
Распрямлюсь, встряхну себя немножко. (распрямляем спину, раздвигаем лопатки,
вытягиваем шею)
…Вам на память перышко оставлю
Мягкое, пушистое в ладошке. (сдуваем с ладошки воображаемое пёрышко, делаем
глубокий вдох и выдох)

Где применяется показательная функция?  С этим нас познакомит Пальчиков Леша.

Применение показательной  функции, презентация

Далее я вам предлагаю поиграть в игру ТАНГРМ. В течение четырех тысячелетий китайская игра танграм служила любимым развлечением в странах Востока, а с начала XIX века она получила распространение и на Западе. Сейчас мы с вами, ребята, тоже будем играть на уроке, но играть мы будем в математический танграм, который поможет нам в закреплении темы: «Показательные уравнения и неравенства».

Каждая группа получает задание разработать макет детской игрушки с заданными параметрами (уравнения и неравенства, которые надо решить).

Полученный макет надо будет представить команде-сопернице (придумать сказку или рекламный стих и т.п.).

Задания для танграма «Свеча»                     Задания для танграма «Заяц»

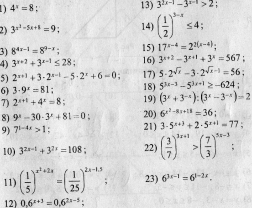
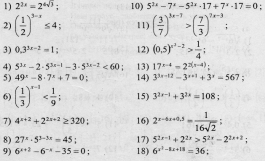
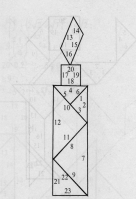
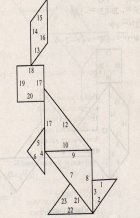
Перед вами решенное уравнение и неравенство, в которых допущены ошибки. Вам нужно найти эти ошибки. Возьмите маркеры и обведите в кружочек ошибку. В каждом выражении и в уравнении только одна ошибка. За ответ 2 балла каждому в группе.

Рефлексия

1. Предлагаю вспомнить,  какая задача стояла перед нами в начале урока? (закрепить   и систематизировать знания   и умения, полученные на предыдущих уроках по этой теме, вспомним определения и формулы, виды и алгоритмы решения показательных  уравнений и неравенств.)

 2. Можно ли считать, что мы справились с нею? (Да)

5. Где вам пригодится знания свойств показательной функции? (для решения уравнений, неравенств, для сдачи ЗНО)

6. Ответьте на такой вопрос, Что ВАМ больше всего запомнилось на уроке?

7. Что для вас было сложным на уроке?   Вы согласны с девизом урока? (Чтобы много знать - нужно много и трудиться)

8. Что дал мне для жизни урок? (когда ты устроишься на работу, ты всегда сможешь применить математические знания)

Давайте запишем домашнее задание:

Повторить §2-3

Решить № 99 и 115 ст. 29

или

• тема 14 (14.24-14.28) ЗНО 2014
• тема 15 (15.26-15.27) ЗНО 2014

Теперь давайте посчитаем сумму ваших баллов  и поставим оценки. У кого высокий балл? Достаточный? Средний? Низкий?

У вас есть кружочки нарисуйте ! если я работал отлично, в полную силу своих возможностей, чувствовал себя уверенно

!? – я работал хорошо, но не в полную силу своих возможностей, испытывал чувство неуверенности, боязни, что отвечу неправильно.

? у меня не было желания работать, сегодня не мой день.

У меня было вот такое настроение, а у вас? Показали мне. Показали гостям.

Дорогие ребята, я вам хочу пожелать ярких впечатлений, здоровья и творчества.

Пусть каждый день и каждый час
Вам новое добудет.
Путь добрым будет ум у вас,
А сердце умным будет.