План практичного заняття №

 

Вид заняття: практичне заняття, тип: формування вмінь і навичок

Тема:  Елементи комбінаторики

Мета заняття :

Вчити розрізняти види сполук і знаходити їх число за  відповідними формулами, розв'язувати нескладні комбінаторні задачі, розвивати креативне мислення, спонукати до пізнавальної активності; виховувати інтерес до математики, нових знань і прагнення їх набути; виховувати духовні цінності.

Методи: репродуктивні, пояснювально – ілюстративні, практичне виконання вправ, бесіда

Матеріально-технічне забезпечення та дидактичні засоби: таблиця, дидактичні матеріали.

 

 

           Структура заняття                                                                Відведений час

1. Організаційна частина: контроль відвідування                                            3 хв

2.Повідомлення теми, формування мети та                                                   2 хв

основних завдань

3. Актуалізація питань  (питання контролю):                                              10 хв 

• Тест-контроль(підготовка до ДПА) усно із взаємоперевіркою
• Гра «Впізнай сполуку!»

4.Контроль вихідного рівня знань студентів:                                            10 хв

    Варіант 1

1. Скількома способами можна вибрати 4 яблука із 10? (3 бали)

2. Скількома способами можна розподілити 3 різних путівки між 25 учнями? (3 бали)

3. Скількома способами можна сформувати поїзд з 8 вагонів? (3 бали)

4. Обчисліть: ++. (3 бали)

Варіант 2

1. Скількома способами можна розподілити 3 однакових путів­ки між 25 учнями? (3 бали)

2. У класі навчається 10 юнаків. Скількома способами можна їх вишикувати у шеренгу? (3 бали)

3. Скількома способами із 20 студентів групи можна обрати го­лову, заступника голови і секретаря зборів? (3 бали)

4. Обчисліть: ++. (3 бали)

Відповіді: В-1. 1. = 219.    2. = 13 800. 3. P₈ - 8! = 40 320.    4. 22.

B-2. 1. = 2300.  2. P₁₀ = 10! = 3 628 800. 3. = 6840.    4. 16.

 

5. Інструктаж вступний

6.Формування умінь і навичок. Перелік практичних                               50 хв

 завдань.   

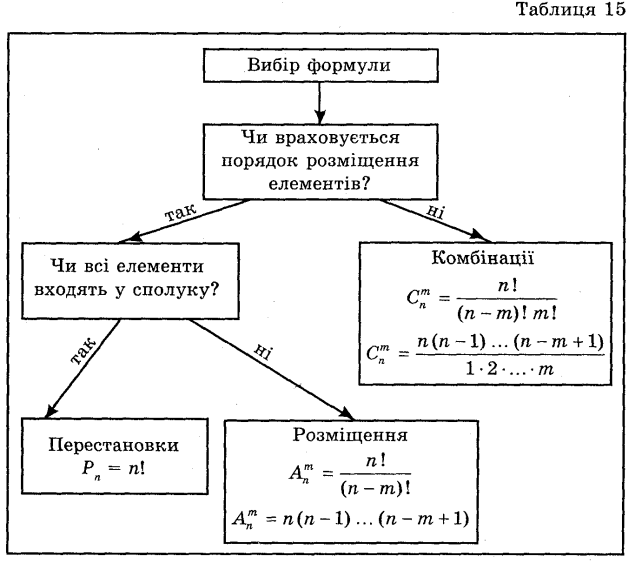
Визначте вид сполуки, про яку йдеться мова в задачі, та за­пишіть відповідну формулу:

1. а) 25 учителів потиснули один одному руки перед педрадою. Скільки було зроблено рукостискань?

б) 25 студентів обмінялися фотографіями так, що кожний обмінявся з кожним. Скільки було роздано фотографій?

Відповіді: а) = 300; б) = 600.

2. а) У класі з 32 учнів вибирають делегацію до шефів, яка скла­дається з трьох осіб. Скільки існує варіантів такого вибору?

б) У класі з 32 учнів для проведення зборів обирають голову, заступника і секретаря. Скількома способами це можна зробити?

Відповіді: а) = 4960; б) = 29 760.

3. а) Біля стола стоїть 9 стільців. Скільки існує способів розмі­щення за столом 9 осіб?

б) 9 дівчат водять хоровод. Скільки існує для них різних ва­ріантів стати в коло?

в) 3 дев'яти різних намистин потрібно зробити намисто. Скільки існує різних способів його утворення?

Відповіді: а) Р₉ = 9!; б) (кількість хороводів у 9 раз менша від Р₉, бо циклічні перестановки не змінюють хоровод); в) (циклічні перестановки не змінюють намисто, а також намисто не зміниться, якщо перевернути його).

Комбінаторні задачі бувають різних видів. Але більшість із них розв'язують за допомогою двох основних правил: правила суми і правила добутку (таблиця 16).

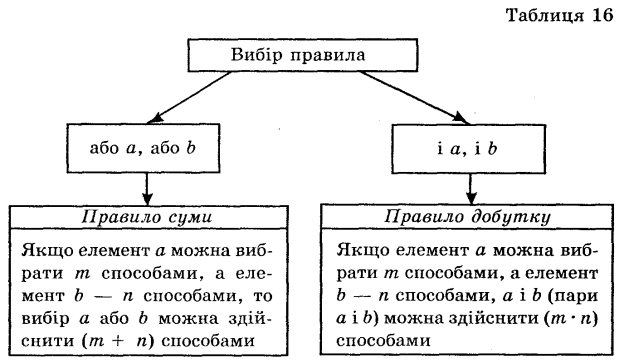
Задача. У класі 12 хлопчиків і 10 дівчаток.

а) Скількома способами можна вибрати одного учня цього класу?

б) Скількома способам двох — хлопчика і дівчинку?

в) Скількома способами можна вибрати дівчинку?

г) Уже вибрано одного учня. Скількома способами можна виб­рати після цього хлопчика і дівчинку?

Розв'язання

а) Хлопчика можна вибрати 12 способами, а дівчинку — 10 спо­собами, тоді за правилом суми або дівчинку, або хлопчика можна вибрати 12 + 10 = 22 (способами).

б) Хлопчика можна вибрати 12 способами, а дівчинку — 10 спо­собами, тоді за правилом добутку і дівчинку, і хлопчика мож­на вибрати 12 · 10 = 120 (способами).

в) Дівчинку можна вибрати 10 способами.

г) Якщо один учень уже вибраний, то можливі два варіанти:

1) якщо був вибраний хлопчик, то хлопчиків залишилося 11, отже існує 11 варіантів його вибору, для дівчинки — 10 варіантів, для пари 11 · 10 = 110 (варіантів).

2) Якщо була обрана дівчинка, тоді дівчаток залишилося 9, отже дівчинку вибрати можна 9 способами, хлопчика — 12 способами, а пару можна вибрати 9 · 12 = 108 (способами), За правилом суми маємо загальну кількість варіантів 11 · 10 + 12 · 9 = 110 + 108 = 218.

Відповіді: а) 22;  6)120;  в) 10; г) 218.

 

Виконання вправ

1. 7 книг різних авторів і трьохтомник одного автора розташо­вані на книжковій полиці. Скількома способами можна роз­ставити ці 10 книжок на полиці так, щоб книги автора трьохтомника стояли поруч?

Відповідь: P₃ · P₈ = 241 920.

2. Збори з 30 осіб обирають голову, секретаря та трьох членів редакційної комісії. Скількома способами це можна зробити?

Відповідь: · = 2 850 120.

3. У підрозділі 60 солдат і 5 офіцерів. Скількома способами мож­на виділити наряд, який складається із трьох солдат і одно­го офіцера?

Відповідь: · = 171100.

4. Із 10 троянд і 8 жоржин треба скласти букет так, щоб в ньо­му були 2 троянди і 3 жоржини. Скількома способами мож­на скласти букет?

Відповідь: · = 2520.

5. Із семи бігунів і трьох стрибунів треба скласти команду із 5 чоловік, в яку б входив хоч би один стрибун. Скількома спо­собами це можна зробити?

Відповідь: + + = 231.

 

7. Поточний контроль виконання роботи                                                       2 хв

Виставлення оцінок за роботу на занятті. за тести

8.Інструктаж заключний

9. Видача завдань для самостійної роботи: придумати по 3 задачі

різної складності                                                                                                    3 хв