Посібний матеріал для учнів 10-11 класів "Практичні поради щодо основних прийомів розвязування показникових рівнянь"
Посібник для учнів з теми "Показникові рівняння. Основні прийоми розвязування показникових рівнянь". Призначений для самостійного доопрацювання учнями теми. Крім учнів 10-11 класів, матеріал буде корисним тим, хто готується до ЗНО з математики.
Практичні поради учням щодо розв'язування показникових рівнянь
- Вступ
Згадаймо, що показниковими називаються рівняння, в яких невідоме міститься в показнику степеня.
Найпростіше показникове рівняння має вигляд:
ах = аb, де а > 0, а ![]() 1, b – число, х - невідоме.
1, b – число, х - невідоме.
Тоді здоровий глузд нам підказує, що якщо степені рівні, і основи цих ступенів також рівні, то показники ступеня теж рівні! І інакше бути не може!
Тобто, якщо ах = аb , то х = b.
Це є основним принципом розв'язування показникових рівнянь.
Що ще необхідно знати при розв'язуванні показникових рівнянь.
Для успішного розв'язування показникових рівнянь головне знати основні властивості степені. Без цього нічого не вийде !!! Також не зайвою буде особиста спостережливість, кмітливість, інтуїція.
Згадуємо основні властивості степеня і ні на хвилину не забуваємо.
- а0 = 1, а1= а.
-
аm/n=
 , де m и n– натуральні числа.
, де m и n– натуральні числа.
-
a-n =

- an · am = an+m
-
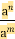 = an-m
= an-m
- (an)m = an·m
- (ab)n = an·bn
-
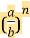 =
= 
-
ax > 0, при всіх a > 0, a
 1 та x
1 та x 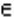 R;
R;
Крім спостережливості та кмітливості стане в нагоді і знання значень деяких степенів. Це допоможе «впізнати» в числі степінь іншого числа.
|
n |
n 2 |
n 3 |
n 4 |
n 5 |
n 6 |
|
2 |
4 |
8 |
16 |
32 |
64 |
|
3 |
9 |
27 |
81 |
243 |
729 |
|
4 |
16 |
64 |
256 |
1 024 |
4 096 |
|
5 |
25 |
125 |
625 |
3 125 |
15 625 |
|
6 |
36 |
216 |
1 296 |
7 776 |
46 656 |
|
7 |
49 |
343 |
2 401 |
16 807 |
117 649 |
|
8 |
64 |
512 |
4 096 |
32 768 |
262 144 |
|
9 |
81 |
729 |
6 561 |
59 049 |
531 441 |
Також зауважимо, що 26= 43= 82 = 64 і 36=93=812 = 729 (за властивістю степеня).
Якщо ж вам не вдається «дізнатися в обличчя», тобто побачити степінь числа, то можна спробувати визначити її самостійно. Треба використати ознаки подільності і розкласти число на прості множники.
2. Прийоми розв'язування різних типів рівнянь
Поки що розглянемо тільки ті показникові рівняння, при розв'язуванні яких (після елементарних перетворень виразів) ми отримуємо самий елементарний вид показникових рівнянь. Тобто коли в обох частинах рівняння залишаються ступеня з однаковими підставами, і нам залишається порівняти показники ступеня.
Розв'язуємо рівняння, що зводяться до найпростіших.
Такі рівняння розв'язуються зведенням обох частин рівняння до степеня з однаковою основою.
А саме: здійснюємо перехід від рівняння af(x) = ag(x) до рівняння
f(x) = g(x)
Розв'яжемо разом:
Приклад 1.
26х - 8х+9 = 0
Зауважимо, що 8 = 23, тоді можемо записати:
26х – (23) х+9 = 0
26х – 2 3х+27 = 0
26х = 2 3х+27
6х = 3х + 27
3х = 27
х = 9
Відповідь: х = 9.
Приклад 2.
![]()
Зауважимо, що 81=34, тоді
![]() 34
34
Прирівнюємо показники степенів:
х2-х-2=4
х2-х-6=0
Тобто маємо квадратне рівняння. Розв'язуємо його.
D=1+24=25, D>0, отже існує два дійсних кореня
х1=(1+5)/2=3
х2=(1-5)/2=-2
Відповідь: х=3, х = - 2
Приклад 3.
![]() =9
=9
![]() запишемо як
запишемо як ![]() , а 9 запишемо як 32. Тоді
, а 9 запишемо як 32. Тоді
![]() = 32
= 32
Отже
![]() = 2
= 2
х = 4
Відповідь: x=4
Приклад 4.
(![]() )x = (
)x = (![]() )5
)5
Зрозуміло, що (![]() )5 можна записати як (
)5 можна записати як (![]() )-5.
)-5.
Тоді
(![]() )x = (
)x = (![]() )-5
)-5
Основи однакові, отже і показники степеня однакові:
x = - 5
Відповідь: x = - 5
Рівняння, що розв'язуються за допомогою винесення за дужки спільного множника
Розв'яжемо разом:
Приклад 1.
4х+1 + 4х=320
У таких випадках виноситься степінь з найменшим показником. В даному рівнянні найменшим показником є х. Виносимо 4х за дужки:
4х(4+1)=320
4х·5=320
Подамо 320 у вигляді 5·43, тоді маємо:
4х·5=5·43
Скорочуємо ліву та праву частину рівняння на 5, маємо:
4х=43
Тоді
х=3
Відповідь: х=3
Приклад 2.
7х+2+4·7х-1=347
Степенем з найменшим показником в цьому рівнянні є 7х-1, отже, за дужки виносимо 7x-1. Маємо:
7х-1· (73+4)=347
7х-1·347=347
Скорочуємо ліву та праву частину рівняння на 347:
7х-1=1
Зауважимо, що будь-яке число в степені 0 дорівнює 1. Отже, запишемо 1 як 70. Тоді
7х-1=70
Отже
х-1=0
х=1
Відповідь: х=1
Розв'язок цього ж рівняння можна записати і інакше.
7х+2+4·7х-1=347
зауважимо, що 7x+2 = 72 · 7х , 7x-1 = 7 х · (1/7 ). Маємо:
72 · 7х + 7 х · (4/7 ) = 347
7х(49 + 4/7) = 347
7х(343/7 + 4/7) = 347
7х(347/7) = 347
Поділимо ліву та праву частину рівняння на 347 та помножимо на 7. Маємо :
7х = 7
Отже
х=1
Відповідь: х=1
«Муха з слона» або рівняння, що розв'язуються за допомогою введення заміни.
Приклад 1.
4х - 5・2х + 4=0
Запишемо 4х як 22х, отримаємо:
22х - 5·2х + 4=0
Вводимо заміну: 2х позначимо як змінну t. Тобто 2х = t, а 22х = t2. Отримаємо:
t2 - 5t + 4=0
За теоремою Віета:
t1=1
t2=4
Тепер повернемось до старої змінної. Замінюємо t на 2х:
- 2х1=1, 2) 2х2=4
Так як 20=1, то
2х1=20
Отже
х1=0
Так як 4=22
2х2 = 22
Отже
х2 = 2
Тобто рівняння має два дійсних кореня: 0 і 2.
Відповідь: х1=0 , х2 =2.
Приклад 2.
5х - 5 2-х = -2
Розпишемо показники степеня:
5х - ![]() = -2
= -2
Вводимо заміну. Нехай 5х = у, тоді
у - ![]() = -2
= -2
Помножимо обидві частини рівняння на у.
у2 - 52 = -2·у
у2 +2 у - 25 = 0
(у - 5)2 = 0
у = 5
Повертаємось до старої змінної: у = 5х
Маємо: 5х = 5, отже х = 1
Відповідь: х = 1
І знову з “слона” робимо “муху”
Рівняння, що містять степінь з двома різними (що не зводяться один до одного) основами.
Приклад 1
3 · 2х + 1 + 2 · 5х – 2 = 5х + 2х – 2.
В цьому рівнянні ми маємо дві різні основи.
Бачимо, що число 5 ми не можемо надати у вигляді степеня числа 2. Отже тепер нам залишається виконати такі перетворення зі степенями, щоб отримати однакові показники степеня.
Щоб уникнути дробів, зведемо степені до показника (х-2).
Зауважуємо, що х+1 = (х-2)+3, а х = (х-2)+2.
3 · 2(х - 2)+3 + 2 · 5х – 2 = 5(х - 2) + 2 + 2х – 2
Тепер скористаємось властивостями степенів і розпишемо їх так:
3 · 2(х - 2)· 23+ 2 · 5х – 2 = 5(х - 2) ·5 2+ 2х – 2
Виконавши обчислення, маємо:
24 · 2х - 2+ 2 · 5х – 2 = 5х - 2 ·25 + 2х – 2
24 · 2х - 2- 2х – 2= 5х - 2 ·25 - 2 · 5х – 2
2х – 2 ·23 = 5х – 2·23
2х – 2 = 5х – 2
Тепер маємо різні основи, але однакові показники степеня.
Ділимо обидві частини рівняння наприклад, на 2х – 2 .
Маємо:
1= (5/2)х– 2
Тоді х – 2 = 0
х = 2.
Відповідь: 2.
Приклад 2
2х · 3х – 3 = 48
Також в цьому рівнянні ми маємо дві різні основи.
Знову виконуємо такі перетворення зі степенями, щоб отримати однакові показники степеня.
Щоб уникнути дробів, зведемо степені до показника (х-3).
Зауважуємо, що х = (х-3)+3.
2(х - 3) + 3 · 3х – 3 = 48
Тепер скористаємось властивостями степенів і розпишемо їх так:
2(х - 3) ·23· 3х – 3 = 48
2х - 3 · 3х – 3 ·8= 48
8·(2· 3)х – 3 = 48
8·6х – 3 = 48
6х – 3 = 6
х-3 =1
х=4
Відповідь: 4
Приклад 3
3 · 22х + 6х + 2· 32х = 6х + 1
В цьому рівнянні ми маємо три різні основи.
Бачимо, що 6=2・3. Отже використаємо це разом з попередніми прийомами. Зводимо всі степені до показника х.
3 · 22х + 2· 32х = 6х + 1- 6х
3 · 22х + 2·32х =(2·3)х · 5
3 · 22х + 2·32х = 2х·3х· 5
Ділимо обидві частини рівнянні на 6х , зауважуючи, що це 2х·3х
Маємо:
3 · (2/3)х + 2·(3/2)х = 5
Введемо заміну. Якщо (2/3)х = у, то (3/2)х = 1/у
Тоді маємо
3у + 2/у = 5
Помножимо обидві частини рівняння на у.
3у2 + 2 = 5·у
3у2 - 5у + 2 = 0
у1=1, у2 = 2/3,
Повертаємось до старої змінної.
(2/3)х = 1, або (2/3)х = 2/3
Отже х = 0, або х = 1.
Відповідь: 0 і 1.
3. Розв'язуємо самостійно
Якщо при самостійному розв'язуванні завдання тобі здається, що ти вже не знаєш що робити далі, згадай саме універсальне і потужне правило рішення всіх математичних завдань:
Не знаєш, що потрібно - роби все, що можна! Дивишся, і вийде.
Розв'яжи рівняння:
- 32х+4 -11·9х = 210
- 4х - 3·2х +2 = 0
- 4x + 2x= 12.
- 6х = 216
- 8х+1 = 0,125
- 2х+3 - 2х+2 - 2х = 48
- 9х - 8·3х = 9
- 2х - 20,5х+1 - 8 = 0
Знайди добуток коренів:
- 23-х + 2х = 9
- 70.13х + 130,7х+1 + 20,5х+1 = -3
- 25х-1 · 33х-1 · 52х-1 = 720х
- 9·2х - 4·3х = 0
Успіху!!!!!!!!!!!!!!!!


про публікацію авторської розробки
Додати розробку
