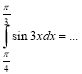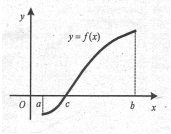Урок " Знаходження площі плоских фігур за допомогою інтеграла"
Розробка уроку на знаходження площ плоских фігур за допомогою інтеграла, в розробці є диференційовна самостійна робота і застосування визначеного інтегралу для обчислення коефіцієнтцу нерівномірного розподілу прибуткового податку.
Навчально – методична карта (план) заняття
Дисципліна Алгебра і початки аналізу
Тема заняття Знаходження площі плоских фігур за допомогою інтеграла
Форма заняття Урок-лекція
Тип заняття Лекція з використанням ТЗН, урок засвоєння нових знань
Навчальна мета заняття Ознайомити студентів з алгоритмом знаходження площ плоских фігур і навчити застосовувати його на практиці; навчити зарисовувати формули для знаходження площ плоских фігур, як суму або різницю площ криволінійних трапецій та знаходити площі плоских фігур; сформувати вміння студентів застосовувати визначений інтеграл до обчислення площ плоских фігур; пригадати побудову графіків елементарних функцій
Розвивальна мета заняття Розвивати можливості проводити аналогію з раніше вивченим матеріалом, розвивати логічне мислення, кмітливість, роз-ширення кругозору учнів
Виховна мета заняття Всесторонньо сприяти розвитку стійкого ін-тересу до математики через вчення із застосуванням інформаційних техно-логій, виховувати графічну культуру
Міжпредметні зв’язки
Дисципліни, які забезпечують алгебра, інформатика,
Дисципліни, які забезпечуються Економіка, будівельна геометрія.
Навчально-методичне забезпечення заняття диск з комп’ютерною презентацією, розробка уроку
Наочність
Технічні засоби навчання комп’ютер, OC Windows 2007, мультемідійний проектор
Література Підручник з Є.П. Нелін, О.Є.Долгова. Алгебра і початки аналізу, 11 клас, 2006 р., Старова О.О. Реалізація між предметних зв’язків на уроках математики. Математика у школах України, №3 2004, Страннікова С.В. Інтегрований урок з геометрії та інформатики. Математика у школах України, №5 2006
, Збірник завдань. Державна підсумкова атестація, ч. 2, 2008.
|
№ п/п |
Зміст заняття |
Хід заняття |
Форми і методи, використані на занятті |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Організація заняття |
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Актуалізація опорних знань |
|
Діалог
Фронтальне опитування
Застосування ІКТ (мультимедійний проектор) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Самоперевірка домашнього завдання |
Викладач пропонує студентам звірити правильність виконання домашніх вправ за записами спроектованими на екран. У разі неспівпадання розв’язку викладач коментує хід розв'язання.(слайд 8-12) |
Застосування ІКТ (мультимедійний проектор) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Закріплення навичок знаходити визначені інтеграли та площу криволінійної трапеції.
Доведення критеріїв оцінювання |
Варіант 1
І. Середній рівень
а) 64; б) 32; в) 160; г) 320.
а) 0; б) 1; в) 2; г) -1.
ІІ. Достатній рівень
а) 1; б) 4; в) -1; г) 2.
а)
в) ІІІ. Високий рівень
а)
в)
Варіант 2
І. Середній рівень
а)
а) 0; б) -1; в) 1; г) 2.
ІІ. Достатній рівень
а) 1; б) 2; в) 3; г) 4.
а)
в) ІІІ. Високий рівень
а)
в)
( 2 бали)
Відповіді: (слайд 13)
|
Самостійна робота (за варіантами), (диференціація навчання)
Самооцінювання (мультимедійний проектор) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Мотивація теми |
Ми живемо в суспільстві де люди мають різні доходи. Чому деякі країни світу більш розвинені, такі як, наприклад, Японія, Німеччина, а є країни в яких дуже низький рівень життя, це – Індія, країни Африки. Від чого це залежить і як це контролювати? Це питання спробував дослідити американський економіст Макс Отто Лоренц. Ним у 1905 році була запропонована Крива Лоренца, як показник нерівності у доходах населення . У такому представленні вона є зображення функції розподілу в якому акумулюються долі чисельності і доходів населення. У прямокутній системі координат крива Лоренца є опуклою вниз і проходить під діагоналлю одиничного квадрата, розташованого в I координатній чверті. Чим більш опуклою буде крива Лоренца, тим більш нерівномірним буде розподіл.
100(1) А
В
O 100(1) x При рівномірному розподілу доходів крива Лоренца співпадає з прямою ОА, тому площа фігури ОАВ між бісектрисою ОА і кривою Лоренца, яка відноситься до площі трикутника ОАС, характеризує степінь нерівності у розподілу доходів населення. Проблемне питання: Як, на вашу думку, обчислити площу заштрихованої фігури? Криві Лоренца застосовують для розподілів не лише доходів, але і майна домогосподарств, часткою ринку для фірм в галузі, природних ресурсів по державах. Зустріти криву Лоренца можна і за межами економічної науки. Сьогодні на занятті ми 1) розглянемо фігури, які обмежені декількома лініями і навчимось знаходити криволінійні трапеції переріз або об’єднання яких є заданою фігурою. 2) запишемо алгоритм обчислення площ плоских фігур і застосуємо набутті знання до розв’язання прикладів. |
Монолог Зв'язок з життям
Мультимедійний проектор (слайд 14)
Зв’язок з економікою. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Зміст і послідовність реалізації питань Пояснення нового матеріалу
Теоретична частина.
Практична частина
Практична частина
|
Площі плоских фігур Сьогодні на занятті ми розглянемо плоші плоских фігур, що обмежені графіками двох неперервних функцій. Існує багато випадків, але ми розберемо найбільш поширеніші. (слайд 15)
Розглянемо перший випадок, коли площа плоскої фігури знаходитиметься через суму площ двох криволінійних трапецій. (Записують)
Зверніть увагу на малюнок на слайді (слайд 16). Спочатку ставиться проблемне запитання до аудиторії: «З яких частин складається дана фігура і як на вашу думку можна знайти площу зображеної фігури?» Викладач пояснює випадок спираючись на зображення слайда, а потім ще раз закріплює пояснення на основі слайда 17. Після чого студенти виконують відповідний малюнок і запис у зошитах.
Розглянемо приклад до даного випадку.
Розв’язання: (записується на дошці із допомогою студентів) Площу заданої фігури розглядатимемо, як суму площ фігури АОВ і трикутника АВС.
Знайдемо точку перетину параболи
Отже,
Тоді
(слайд 19, 20) Отже ми з вами отримали другий випадок, коли фігура обмежена кривою, що задана функцією , віссю Ох і прямими х=а і х=b, але розташована ця фігура по різні сторони відносно вісі Ох. (слайд 21) (виконують малюнок і запис у зошити)
Задача. (слайд 22) За малюнком знайти площу плоскої фігури. Перевірка правильність виконання з обговоренням за слайдом 23. (в процесі розв’язання виконують запис у зошитах)
За слайдами 24, 25, 26 розглядається третій випадок знаходження площі плоскої фігури. На основі робиться висновок про знаходження площі фігури в даному випадкові за слайдом 27.(записують і виконують малюнки) На основі розглянутих випадків можна скласти загальний алгоритм для знаходження площ плоских фігур обмежених двома неперервними функціями. (слайд 28, роблять конспект в зошитах) Алгоритм обчислення площ плоских фігур:
За малюнком виконати завдання. Знайти площу фігури обмежену лініями у=х, у=7-х, х=1, х=3.(слайд 29)
Задача. Обчислити площу фігури, обмеженої лініями
Задача. Обчислити площу фігури, обмеженої лініями
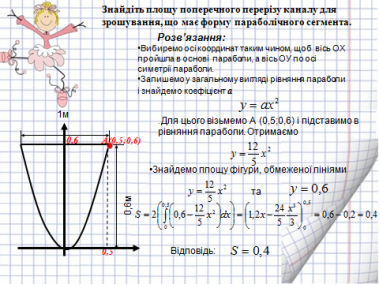
Задача будівельно-географічного змісту.(слайд 32) Знайдіть площу поперечного каналу для зрошування, що має форму параболічного сегмента.
|
Монологічна, діалогічна, з використанням ІКТ ( мультиме-дійний проектор), конспект.
Проблемно-діалогічний метод
Проблемно-діалогічний метод, колективне розв’язання завдання, застосування ІКТ (мультимедійний проектор)
Проблемна ситуація «Працюй мозком!» Проблемно-діалогічний метод, колективне розв’язання завдання, застосування ІКТ (мультимедійний проектор)
Самостійне виконання завдання, застосування ІКТ (мультимедійний проектор)
Проблемно-діалогічний метод, застосування ІКТ (мультимедійний проектор)
Евристична бесіда
Проблемно-діалогічний метод, колективне розв’язання, застосування ІКТ (мультимедійний проектор)
Проблемно-діалогічний метод, колективне розв’язання, мультимедійний проектор
Колективна робота при розв’язуванні задач. Робота біля дошки, застосування ІКТ (мультимедійний проектор)
Зв’язок з будівництвом
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Питання по осмисленню вивченого матеріалу |
|
Індивідуальна робота. Тестування з самоперевіркою, застосування ІКТ (мультимедійний проектор). (слайд 33-40) |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Підведення підсумків заняття |
Під час лекції ми ознайомилися з фігурами, які обмежені декількома функціями і навчилися знаходити їх площі, закріпили вміння обчислювати визначені інтеграли, а також дізналися про цікавий зв’язок таких фігур із життям людини. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Домашнє завдання |
|
Слайд 41 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Склала викладач: Ужва О.О.
ДОДАТОК 1
Знаходження коефіцієнту нерівномірного розподілу прибуткового податку.
Нехай у є частина загального прибуткового податку пропорційна частині х усього населення держави.
Наприклад, якщо ![]() , а
, а ![]() , то це означає , 50% населення сплачує 25% загального прибуткового податку.
, то це означає , 50% населення сплачує 25% загального прибуткового податку.
У загальному випадку х та у – дробові частини цілого (![]() ) і у є функцією х, тобто
) і у є функцією х, тобто ![]() .
.
Будемо вважати, що немає осіб, які не сплачують прибуткового податку, тобто ![]() і весь прибутковий податок сплачує 100% населення,
і весь прибутковий податок сплачує 100% населення, ![]() .
.
Графік функції ![]() , яка описує дійсний розподіл прибуткового податку, називають кривою Лоренца.
, яка описує дійсний розподіл прибуткового податку, називають кривою Лоренца.
 Припустимо, що крива Лоренца задана рівнянням
Припустимо, що крива Лоренца задана рівнянням ![]() .
.
Коли х=0,2, маємо ![]()
Це означає, що 20% населення сплачує 5% загального податку.
Коли х=0,5, маємо ![]()
![]()
![]() Це означає, що 50% населення сплачує тільки 26,56% податку.
Це означає, що 50% населення сплачує тільки 26,56% податку.
Коефіцієнтом нерівності розподілу податку кривої Лоренца називають відношення площі фігури, обмеженої кривою Лоренца та прямою у=х до площі фігури, що лежить нижче прямої у=х.
Задача:
Розподіл прибуткового податку деякої країни здійснюється за кривою Лоренца ![]() , х- частина населення, що сплачує податки, а у відповідна частина загального податку. Яку частину загального податку сплачують 20% найбіднішого населення? Знайти коефіцієнт нерівності Лоренца.
, х- частина населення, що сплачує податки, а у відповідна частина загального податку. Яку частину загального податку сплачують 20% найбіднішого населення? Знайти коефіцієнт нерівності Лоренца.
Розв’язання:
1) Знайдемо частину загального податку , яку сплачують 20% населення, тобто х=0,2
![]()
Це означає, що 20% населення сплачує 4,8% загального податку.
- Знайти коефіцієнт нерівності Лоренца.
Побудуємо в одній системі координат пряму у=х і криву Лоренца ![]() .
.
 у
у
А
1
у=х
![]()
m
C
0 1 х
L=![]() ,
, ![]() ,
, ![]()
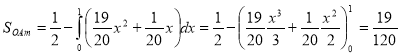
L=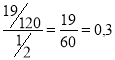
Достатньо низьке значення показує, що прибутковий податок розподілено більш рівномірно.
ДОДАТОК 2
Самостійна робота
Варіант 1
І. Середній рівень
-
Обчисліть інтеграл
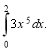 ( 2 бали)
( 2 бали)
а) 64; б) 32; в) 160; г) 320.
-
Обчисліть інтеграл
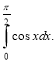 ( 2 бали)
( 2 бали)
а) 0; б) 1; в) 2; г) -1.
- Яка з фігур не є криволінійною трапецією? (2 бали)
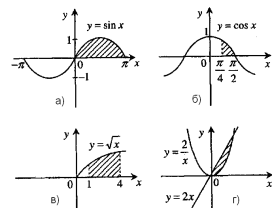
ІІ. Достатній рівень
-
Обчисліть інтеграл
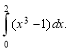 (1,5 бали)
(1,5 бали)
а) 1; б) 4; в) -1; г) 2.
- Площа фігури, зображеної на мал. а), дорівнює:
а) ![]() б)
б) ![]()
в)![]() г)
г)![]() (1,5 бали)
(1,5 бали)
ІІІ. Високий рівень
а) 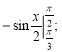 б)
б) 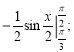
в)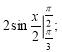 г)
г)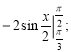 ( 2 бали)
( 2 бали)
Варіант 2
І. Середній рівень
-
Обчисліть інтеграл
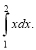 (2 бали)
(2 бали)
а) ![]() ; б)
; б) ![]() ; в)
; в) ![]() ; г)
; г) ![]() .
.
-
Обчисліть інтеграл
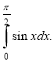 (2 бали)
(2 бали)
а) 0; б) -1; в) 1; г) 2.
- Яка з фігур не є криволінійною трапецією? (2 бали)
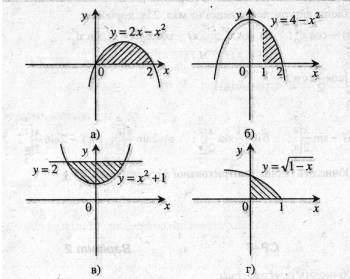
ІІ. Достатній рівень
-
Обчисліть інтеграл
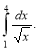 (1,5 бали)
(1,5 бали)
а) 1; б) 2; в) 3; г) 4.
- Площа фігури, зображеної на мал. б), дорівнює:
а) ![]() б)
б) ![]()
в) ![]() г)
г) ![]() (1,5 бали)
(1,5 бали)
ІІІ. Високий рівень
а) 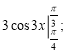 б)
б) 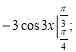
в) 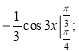 г)
г) 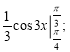
(2 бали)
ДОДАТОК 3
ЛИСТ ОЦІНЮВАННЯ
ПІ студента_____________________________________ Група ____________
САМОСТІЙНА РОБОТА
Варіант ____________
Таблиця відповідей
|
|
а |
б |
в |
г |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Отримана кількість балів:____________
ТЕСТОВІ ЗАВДАННЯ (підсумок засвоєння знань)
під кожним малюнком записати формулу для обчислення площі заштрихованої фігури(за кожну вірну формулу 2 бали)
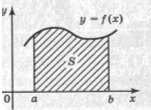
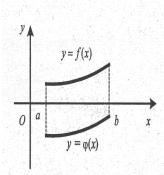
Sф=___________________ Sф=___________________
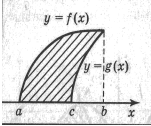

Sф=___________________ Sф=___________________
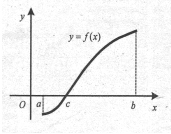
Кількість набраних балів___________
Сума балів за СР і Тести__________
Середня оцінка__________________
Sф=___________________


про публікацію авторської розробки
Додати розробку