Урок № 36 Алгебра 11 клас Тема: "Логарифми та їх властивості"
Алгебра 11 клас А.Г.Мерзляк, Д.А.Номіровський
Урок № 36
Тема: Логарифми та їх властивості
Мета: сформувати поняття логарифма числа, десяткового логарифма; домогтися засвоєння властивостей логарифмів; сформувати вміння розв’язувати задачі, що передбачають використання означення та властивостей логарифмів. Розвивати логічне мислення та уяву. Виховувати старанність та наполегливість у вивченні алгебри.
Тип уроку: засвоєння нових знать та вмінь.
ХІД УРОКУ
І. Організаційний етап
Привітання;
Перевірка присутніх;
Оголошення теми і мети уроку.
ІІ. Перевірка домашнього завдання
- Перевірка завдання, заданого за підручником
ІІІ. Актуалізація опорних знань
Виконання усних вправ
1. Обчисліть: ![]() ;
; ![]()
2. До якого степеня треба піднести: а) число 2, щоб дістати 8; б)число 3, щоб дістати ![]() ; число 32, щоб дістати 2? (3, -2,
; число 32, щоб дістати 2? (3, -2, ![]() )
)
3. Чому дорівнює х, якщо:
а) ![]() б)
б) ![]() в)
в) ![]()
IV. Вивчення нового матеріалу
План
- Означення логарифма числа.
Логарифмом додатного числа b за основою а, де а > 0, а ≠ 1, називається показник степеня, до якого треба піднести число а, щоб одержати число b.
Наприклад: log28 = 3, оскільки 23 = 8;
log2 ![]() = – 2, оскільки 2-2 =
= – 2, оскільки 2-2 = ![]() ;
;
log7l = 0, оскільки 70 = 1.
- Означення десяткового логарифма.
Десятковими логарифмами називаються логарифми за основою 10, позначаються lg.
Наприклад: lg100 = 2, lg0,0001 = - 4.
- Основна логарифмічна тотожність.
Означення логарифма можна коротко записати так:![]() .Ця рівність справедлива при b > 0, a > 0, a ≠ 1 називається основною логарифмічною тотожністю.
.Ця рівність справедлива при b > 0, a > 0, a ≠ 1 називається основною логарифмічною тотожністю.
Наприклад: ![]() ,
,![]() .
.
- Властивості логарифмів:
- Логарифм одиниці за будь – якою основою дорівнює нулю logа 1 = 0.
Наприклад: log6 1 = 0.
- Логарифм числа за основою, що дорівнює цьому числу, дорівнює одиниці
logаa = 1.
Наприклад: log6 6 = 1.
- Логарифм добутку додатних чисел дорівнює сумі логарифмів множників
logа xy = logа x + logа y.
Наприклад: log6 6∙36 = log6 6+ log6 36=1+2=3.
-
Логарифм частки додатних чисел дорівнює різниці логарифмів діленого і дільника logа
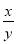 = logа x – logа y.
= logа x – logа y.
Наприклад: log2![]() = log2 8 – log2 4=3-2=1.
= log2 8 – log2 4=3-2=1.
- Логарифм степеня дорівнює добутку показника степеня на логарифм основи цього степеня logа х р = p logа x.
Наприклад: log2 8 3 = 3 log2 8=3∙3=9.
- Формула переходу до логарифмів з іншою основою
loga x =![]() (b > 0, b ≠ 1).
(b > 0, b ≠ 1).
Наслідок 1: ![]() (a > 0, a ≠ 1 , x > 0, x ≠1).
(a > 0, a ≠ 1 , x > 0, x ≠1).
Наслідок 2: ![]() (a > 0, a ≠ 1 , x > 0, p ≠ 0).
(a > 0, a ≠ 1 , x > 0, p ≠ 0).
V. Засвоєння нових знань і вмінь
Робота з підручником
№ 19.1. Чи є правильною рівність:
-
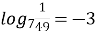 ; (
; ( 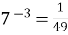 ,
, 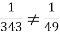 )
)
-
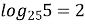 ; (
; ( 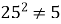 )
)
-
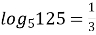 ; (
; ( 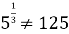 )
)
-
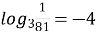 ; (
; ( 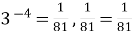 )
)
-
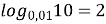 ; (
; ( 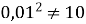 )
)
-
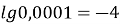 ; (
; ( 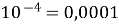 )
)
-
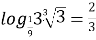 ; (
; (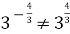
-
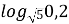 =
= 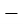 2. (
2. ( 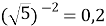 , 0,2 = 0,2)
, 0,2 = 0,2)
№ 19.2. Знайдіть логарифм з основою 2 числа:
-
1; (
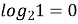 )
)
-
2; (
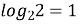 )
)
-
32; (
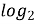 32 = 5 )
32 = 5 )
-
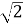 ; (
; (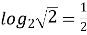 )
)
-
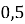 ; (
; (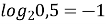 )
)
-
 ; (
; (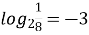 )
)
-
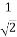 ; (
; (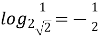 )
)
-
2
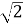 . (
. (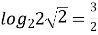 )
)
№ 19.4. Знайдіть логарифм з основою ![]() числа:
числа:
-
1; (
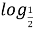 1
1
-
2; (
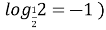
-
8; (
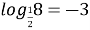 )
)
-
0,25; (
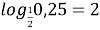 )
)
-
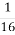 ; (
; (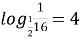 )
)
-
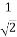 ; (
; (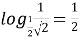 )
)
-
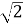 ; (
; (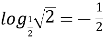 )
)
-
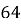 . (
. (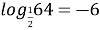 )
)
№ 19.6. Знайдіть десятковий логарифм числа:
- 1; ( lg1=0 )
- 10; ( lg10=1 )
- 100; ( lg100=2 )
- 1000; ( lg1000=3 )
- 0,1; ( lg0,1=−1 )
- 0,01; ( lg0,01=−2 )
- 0,00001; ( lg0,00001=−5 )
- 0,000001. ( lg0,000001=−6 )
VI. Підбиття підсумків уроку
Запитання до класу:
- Означення логарифма числа.;
- Означення десяткового логарифма;
- Основна логарифмічна тотожність;
- Властивості логарифмів.
VIІ. Домашнє завдання
Опрацювати § 19 Виконати № 19.3; 19.5.


про публікацію авторської розробки
Додати розробку
