Урок 6 клас "Прості і складені числа"

УРОК

6 клас

Тема: Прості та складені числа

Мета: формувати вміння і навички учнів за­стосовувати ознаки поділь-ності до розв’язування вправ; розглянути поняття простого та скла­деного чисел; розвивати увагу, логічне мислення; виховувати охайність.

Обладнання. Набір кольорових карток, картки для самостійної роботи, картки з числами.

ХІД УРОКУ

I. Організаційний момент.

Учні-консультанти доповідають про наявність домашніх робіт, роздають кольорові картки кож­ному учню.

II. Актуалізація опорних знань.

Гра «На яке число ділиться дане число»

На дошці написано, який дільник відповідає кольору:

Жовтий          — 2.

Зелений         — 5.

Білий            — 10.

Червоний      — 3.

Синій           — 9.

Учитель піднімає по черзі картки з числами: 32, 625, 700, 336, 27, 603, 320, 404, 708, 125, 123, 2610, 115.

Учні піднімають картку того кольору, що від­повідає числу, на яке ділиться дане число. Кар­ток буде кілька, коли дане число має кілька діль­ників.

III. Оцінювання знань і вмінь учнів.

Самостійна робота

Варіант 1

1. Запишіть три дільники числа 20.

2. Випишіть числа, що діляться на 2; на 5; на 9: 32, 35, 48, 88 011, 125, 342, 2340.

3.  Які з цифр можна підставити замість зі­рочки, щоб число 451* ділилося на 3, але не ділилося на 5?

4. Запишіть найбільше трицифрове число, яке при діленні на 5 дає остачу 1.

Варіант 2

1. Запишіть три дільники числа 30.

2. Випишіть усі числа, які діляться на 2; на 3; на 10:

30, 52, 76, 670, 210, 342, 2340.

3.  Які з цифр можна підставити замість зі­рочки, щоб число 841* ділилося на 3, але не ділилося на 5?

4.  Запишіть найбільше чотирицифрове чис­ло, яке при діленні на 3 дає остачу 1.

(Кожне завдання самостійної роботи оціню­ється 3 балами.)

ІV. Сприймання і засвоєння нового матеріалу.

Кожен учень отримує картку, де в першій ко­лонці таблиці дано десять чисел:

1, 2, 3, 4, 5, 6, 12, 17, 43, 60

(1, 2, 3, 4, 5, 10, 23, 35, 96, 111;

1, 2, 3, 8, 9, 11, 12, 19, 36, 61;

1, 2, 3, 7, 15, 29, 48, 57, 61, 100) та заповнює її другу і третю колонки картки.

Зразок картки

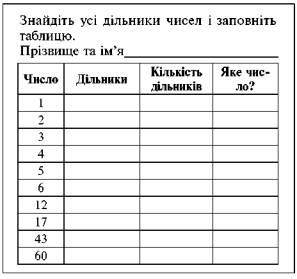
Учитель формулює означення простого та складеного чисел, після цього учні заповню­ють четверту колонку. Особливу увагу потрібно приділити числу 1.

Історична довідка

(Підготував учень.)

Прості числа привертали увагу стародавніх математиків. Адже кожне число, крім одиниці, або є простим, або розкладається в добуток про­стих чисел.

Виникало природне запитання: чи існує най­більше просте число? На це запитання дав від­повідь давньогрецький математик Евклід, який довів у своїй праці «Начала», що для кожного простого числа існує більше від нього просте число. Знаходити всі прості числа, які не пе­ревищують даного натурального числа, вміли ще понад дві тисячі років тому. Давньогрецький учений Ератосфен — один з найдосвідченіших математиків свого часу — застосовував для цьо­го спосіб «решета», за яким тривалий час від­шукували прості числа.

Досконаліші способи знаходити прості числа розробили вчені тільки в ХХ ст. Було складено чимало таблиць простих чисел. Тепер пошук простих чисел ведуть за допомогою комп’ютерів. Знайдено, зокрема, просте чис­ло, яке складається із 750 цифр, і навіть просте число з 1000 цифр (щоб записати таке довге число, потрібна паперова стрічка завдовжки 3 метри).

Ще в давнину вчених цікавило питання, за яким законом розміщені прості числа в натуральному ряді. Але відтоді як Евклід до­вів, що не існує найбільшого простого числа, спливло понад 2 тисячі років, а закону роз­міщення простих чисел досі не знайдено. З од­ного боку, є прості числа, які відрізняються одне від одного на 2, — так звані «числа-близ-нюки», наприклад 5 і 7, 11 і 13, 17 і 19. З ін­шого боку, якщо розмістити всі прості числа за зростанням, то, і це доведено, серед них завжди можна знайти два простих числа, різ­ниця між якими є більшою від будь-якого заданого числа.

Жодної закономірності не виявлено і віднос­но кількості простих чисел у певних інтервалах. Проте для обчислення кількості простих чисел у ряді натуральних чисел від 1 до n формулу знайти вдалося. Її вивів у XIX ст. російський учений П. Л. Чебишов.

У підручнику наведено прості числа від 2 до 997.

V. Закріплення вивченого матеріалу.

Усні вправи: № 84, 85, 86, 94.

Письмові   вправи:  № 88, 90, 92 (скористайтесь ознаками подільності), № 100.

VI. Підсумки уроку.

Учитель. Сьогодні ми вивчили прості та скла­дені числа.

1. Яке число називають простим?

2. Яке число називають складеним?

3.  Що можна сказати про числа 1 та 0, чим вони цікаві?

VII. Домашнє завдання. § 1, п. 4. Група А: № 89, 91, група Б: № 93, 96. Підготувати запитання з вивченого матеріалу до гри «Футбол».