Урок 80 Контрольна робота з алгебри № 5 за темою: «Основи комбінаторики, теорії ймовірностей та статистики», 9 клас
Урок 80 Контрольна робота з алгебри № 5 за темою: «Основи комбінаторики, теорії ймовірностей та статистики», 9 клас
Мета:навчальна: перевірити рівень засвоєння знань з теми;
розвивальна: формувати вміння логічно мислити; правильно висловлювати власні думки в письмовому вигляді;
виховна: виховувати дисциплінованість, самостійність, відповідальність.
Тип уроку: контроль знань і вмінь.
Хід уроку
І. Організаційний етап
Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу. Доцільно нагадати учням правила поведінки під час проведення контрольної роботи. На цьому етапі уроку можна ознайомити учнів зі структурою та критеріями оцінювання контрольної роботи.
IІ. Текст контрольної роботи
І варіант
- Оркестру потрібні скрипаль, альтист і піаніст. На місце скрипаля є 6 кандидатів, на місце альтиста — 4, а на місце піаніста — 3. Скільки існує варіантів нового складу оркестру?
А) 3 Б) 6 В) 13 Г) 72 Д) 144
- Ганна вирішила купити або морозиво, або тістечко. У магазині морозиво було трьох видів, а тістечка — п’яти видів. Скількома способами Ганна може здійснити покупку?
А) 2 Б) 15 В) 8 Г) 5 Д) 3
-
У ящику лежать 8 яблук, три з яких червоні, а решта — зелені. Яка ймовірність того, що вибране навмання яблуко буде не зеленим?
А)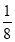 Б)
Б) 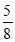 В)
В) 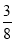 Г)
Г) 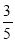 Д) 5
Д) 5
- На кожній із чотирьох однакових карток записано одну з літер: Н, Е, Б, О. Яка ймовірність того, що картки, навмання розкладені в рядок, утворять слово НЕБО?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]() Д)
Д) ![]()
- Олена забула останні дві цифри телефону подруги, але пам’ятає, що вони різні. Знайдіть імовірність того, що з першої спроби вона правильно набере телефон подруги.
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]() Д)
Д) ![]()
- Під час зустрічі 16 осіб потиснули один одному руки. Скільки всього зроблено рукостискань?
А) 16 Б) 32 В) 256 Г) 240 Д) 120
- Скільки шестицифрових чисел можна скласти з цифр 0, 1, 2, 3, 4, 5, якщо усі цифри числа різні?
- Дано вибірку: 4; 7; 3; 9; 7; 5; 6; 7; 3; 8. Знайдіть її моду, медіану і середнє значення.
-
У коробці лежать кульки, з яких 20 — чорні, а решта — білі. Скільки в коробці білих кульок, якщо ймовірність того, що вибрана навмання кулька виявиться білою, становить
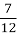 ?
?
ІІ варіант
- Яринка вирішила купити або цукерки, або печиво. У магазині цукерки були шести видів, а печиво — трьох видів. Скількома способами Яринка може здійснити покупку?
А) 2 Б) 18 В) 6 Г) 9 Д) 3
-
Маємо 8 різних конвертів, 4 різні марки і 6 різних листівок. Скількома способами можна вибрати комплект з конверта, марки і листівки?
А) 3 Б) 182 В) 192 Г) 18 Д) 8 - На кожній із трьох однакових карток записано одну з літер: М, И, Р. Яка ймовірність того, що картки, навмання розкладені в рядок, утворять слово МИР?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]() Д)
Д) ![]()
-
У коробці лежать 9 стрічок, дві з яких червоні, а решта — сині. Яка ймовірність того, що вибрана навмання стрічка буде не червоною?
А)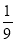 Б)
Б) 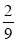 В)
В) 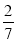 Г) 7 Д)
Г) 7 Д) 
- Група учнів із 20 осіб вирішила обмінятися фотокартками. Скільки всього фотокарток потрібно для цього?
А) 380 Б) 400 В) 40 Г) 190 Д) 20
- З натуральних чисел від 1 до 18 учень навмання називає одне. Яка ймовірність того, що це число є дільником числа 18?
А) ![]() Б)
Б) ![]() В)
В) ![]() Г)
Г) ![]() Д)
Д) ![]()
- Скільки п’ятицифрових чисел можна скласти з цифр 0, 1, 2, 3, 4, якщо усі цифри числа різні?
- Дано вибірку: 3; 8; 5; 3; 6; 8; 9; 2; 8; 10. Знайдіть її моду, медіану і середнє значення.
-
У ящику лежать кульки, з яких 12 — білих, а решта — червоні. Скільки в ящику червоних кульок, якщо ймовірність того, що вибрана навмання кулька виявиться червоною, становить
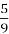 ?
?
ІІІ. Підсумки уроку
Після того як будуть зібрані зошити, можна відповісти на запитання учнів, які виникли під час виконання контрольної роботи.
VI. Домашнє завдання
Виконати завдання протилежного варіанту контрольної роботи.


про публікацію авторської розробки
Додати розробку
