Урок алгебри 8 клас "Розв'язування квадратних рівнянь за формулою"

Урок № 64

Алгебра 8 клас

Дата:

Тема уроку. Формула коренів квадратного рівняння

Мета уроку:

Навчальна: закріплення та систематизація розв’язування квадратних рівнянь за формулою. Розвивати навички розв’язування рівнянь, які зводяться до квадратних.

Розвивальна: розвивати навички обчислень, математичну мову, абстрактне та логічне мислення.

Виховна: виховувати культуру запису, повагу до думки товаришів.

Тип уроку: застосування знань та вмінь.

Наочність та обладнання: Опорний конспект «Квадратні рів­няння», підручник «Алгебра», А.Г. Мерзляк, 2016 р., проектор, презентація, комп’ютер.

Хід уроку

1. Організаційний етап

Перевірити готовність учнів до уроку, налаштувати на роботу.

 

2. Перевірка домашнього завдання

1. Перевірити д/з, задане за підручником, відовісти на запитання по домашній роботі.
2. Математичний диктант

 

Варіант 1	Варіант 2
1. Розв'яжіть рівняння
х2 – 8х – 9 = 0	х2 – 8х + 7 = 0
виділенням квадрата двочлена
2. Обчисліть дискримінант рівняння
3х2 – 8х – 3 = 0	2х2 – 3х – 2 = 0
3. Знайдіть корені рівняння:
3х2 – 8х – 3 = 0	2х2 – 3х – 2 = 0
4. За якої умови деяке повне квадратне рівняння
має один корінь (два рівних дійсних корені)?	не має дійсних коренів?
5. Скільки коренів має рівняння:
х2 – 10х + 25 = 0?	х2 + 6х + 9 = 0?

 

III. Формулювання мети і завдань уроку

Вивчення окремих випадків застосування формул коренів квадратного рівняння та оволодіння вміннями їх використовувати визначаємо як провідну мету уроку.

 

 

3. Актуалізація опорних знань та вмінь

Вправа «Мікрофон»

• Які рівняння називають квадратними?
• Як називають а, в, с в квадратному рівнянні?
• Які рівняння називають зведеними квадратними?
• Які це неповні квадратні рівняння? Скільки їх видів?
• Наведіть приклади неповних квадратних рівнянь, скільки вони мають коренів?
• Чому дорівнює дискримінант квадратного рівняння?
• Як залежить кількість коренів квадратного рівняння від дискримінанта?
• Чому дорівнюють корені квадратного рівняння?
• Як розв’язати за формулою повне квадратне рівняння. Якщо в ньому другий коефіцієнт число парне?

Виконання усних вправ

1. Укажіть у квадратному рівнянні його коефіцієнти:

а) 3у² – 5у + 1 = 0; б) -х² + х – 3 = 0; в) 12t – 7t² + 4 = 0; г) 9t – 6 + t² = 0;

д) 5т – т² = 0; є) п² – 7 = 0.

2. Спростіть вирази: 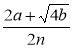; (2k)² – 4ат.
3. Скільки коренів має квадратне рівняння:

x² – 64 = 0; у² + 49 = 0; 2р² – 7р = 0; k² = 0; 2х² + 4х – 1 = 0;

х² + 3х + 4 = 0; у² + 3у + 2= 0.

 

в розв'язуванні опорного завдання вимагати строгого її дотримання.

 

V. Формування вмінь

 

Виконання письмових вправ

Для реалізації дидактичної мети уроку слід розв'язати завдання та­кого змісту:

1. Розв'язування квадратного рівняння за формулами.

1) Розв'яжіть рівняння:

а) х² – 2х – 1 = 0; б) 7х² – 18х + 8 = 0; в) 3х² + 22х – 16 = 0;

г) х² + 21х + 90 = 0; д) 3х² + 53х – 18 = 0; є) -25х² + 50х + 75 = 0;

ж) х² + 0,5х – 1,5 = 0; з) 2х² – х + = 0; и) х² – х – = 0.

2) Розв'яжіть рівняння:
а) 3х² – 14х + 16 = 0; б) 5х² – 16х + 3 = 0; в) х² + 2х – 80 = 0;

г) х² – 22х – 23 = 0; д) 4х² – 36х + 77 = 0; є) 15у² – 22у – 37 = 0;

ж) 7z² – 20z + 14 = 0; з) у² – 10у – 25 = 0.

За підручником Мерзляк та ін., 2016 року

№ 636, 638, 640, 659 (колективно, коментовано)

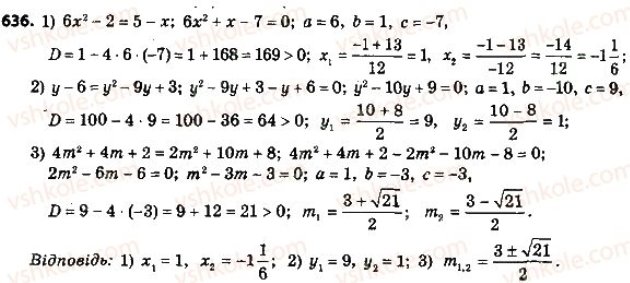
Робота в парі:

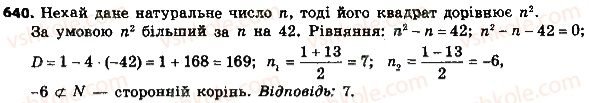
Високий рівень

2. Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань. Вставте пропущений вираз.

 

	х ≥ 3	х – 3
	х ≤ 2	?

 

VII. Підсумки уроку

В якому випадку правильно знайдено корені?

а) х² – 2х – 8 = 0, D₁ = 1 + 8 = 9, , х₁ = , х₂ = ;

б) х² + 2х – 8 = 0, D₁ = 2 + 8 = 10, ;

в) x² – 4х – 12 = 0, D₁ = 4 + 12 = 16, х_1,2 = 2 ± 4, х₁ = 6, х₂ = -2.

Рефлексія

• Що нового ви дізналися на уроці?
• Чи навчилися ви розв’язувати квадратні рівняння за формулою?

 

VIII. Домашнє завдання

Повторити формули

№№ 637, 639, 642, 660.