Урок + презентація "Функція у = х2 , її властивості та графік"

Тема: Функція у = х² ,  її властивості та графік

Мета:

•  домогтися засвоєння учнями властивостей функції у = х² і властивостей її графіка та способу застосування графіка функції у = х² для графічного розв'язання рівнянь виду х² = а;
• формувати вміння аналізувати інформацію, бачити закономірності, сприяти розвитку уваги, логічного та абстрактного мислення;
• виховувати  цілеспрямованість, ініціативність, наполегливість, інтерес до вивчення математики.

Тип уроку: засвоєння нових знань.

Обладнання: підручник, мультимедійна презентація.

Хід уроку:

І. Організаційний етап

Обговорити :

•                  орієнтовний план вивчення розділу «Квадратні корені. Дійсні числа »;
•                  кількість навчальних годин; приблизний зміст матеріалу;
•                  основні вимоги до знань та вмінь учнів;

 

ІI.  Повідомлення теми та мети уроку. Мотивація навчальної діяльності

Видатний французький філософ, вчений Блез Паскаль стверджував: "Величність людини в його здатності думати". Сьогодні ми спробуємо почути себе великими людьми, відкриваючи знання для себе.

Девізом до  уроку будуть слова древньогрецького математики Фалеса:

              – Що є найбільше у світі? – Простір.

•                 Що найшвидше? – Розум.
•                 Що наймудріше? – Час.
•                 Що приємніше всього?  – Досягнути бажаного.

Хочеться, щоб кожен з вас на сьогоднішньому уроці досяг бажаного результату.

ІII.  Актуалізація опорних знань

 Вправа «Шифрограма»

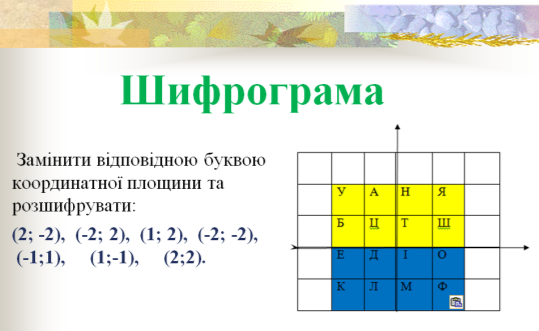Зараз ми пригадаємо і повторимо  вивчений раніше матеріал, а по якій темі – ви дізнаєтесь, розшифрувавши її назву. Потрібно кожну пару чисел замінити відповідною буквою.

 

 

 

 

 

 

 

 

 

 

(2;-2)	(-2;2)	(1;2)	(-2;-2)	(-1;1)	(1;-1)	(2;2)

 Розшифроване слово «Функція»

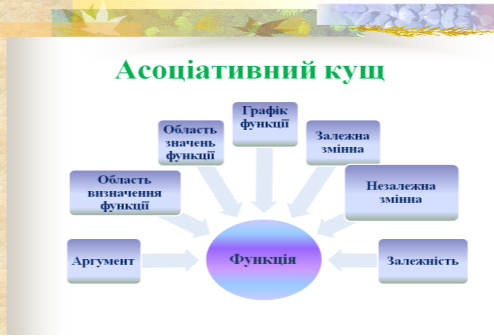
Вправа «Асоціативний кущ»

Назвіть математичні терміни, що асоціюються зі словом «функція» та дайте визначення кожному з них.

 

Математична розминка ( фронтальне опитування)

1. Знайдіть область визначення функції:

а) ; б) ; в) .

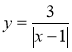2. Функцію задано формулою .

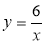     а) Якого значення набуває функція, якщо аргумент дорівнює 4?

      б) При якому значенні аргументу значення функції дорівнює ?

3. Чи проходить графік функції 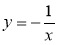через точки:

а) А(-1; 1); б) В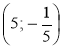; в) С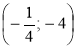; г) D?

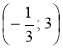4. Визначте знак виразу: а) (-3)¹⁰; б) (-x – 1)² ; в) -x² – 1.

 

  ІV.  Сприймання та первинне усвідомлення  нового матеріалу

 

Проблемна ситуація

« Не розв'язуючи рівняння, доведіть, що рівняння х² = а (де а — деяке число) може мати або два, або один корінь, або не мати жодного кореня, залежно від значення числа а. Дослідіть цю залежність ». (учні обговорюють  завдання, пропонують способи  дослідження). Перед нами постало  питання про необхідність вивчення властивостей функції у = х²  та побудову її графіка.

За словами  французького письменника Оноре де Бальзака «Ключем до кожної науки є знак питання». Тому ми зараз проведемо невелике математичне дослідження і спробуємо відповісти на питання: що являє собою функція у = х² ?; які властивості вона має?; як виглядає її графік? Всі результати дослідження будуть вписані в протокол дослідження.

(У кожного учня  на парті спеціальний бланк).

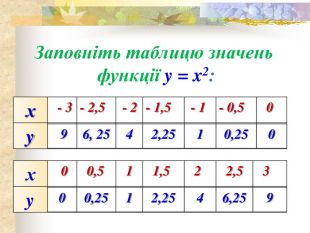
    ● Роботу почнемо з того, що складемо таблицю відповідних значень x і y  функції у = х² .

   Діти самостійно заповнюють таблицю, можна використовувати таблицю квадратів двозначних чисел.

 

x	- 3	-2,5	- 2	-1,5	- 1	-0,5	0	0,5	1	1,5	2	2,5	3
y

Перевірте ваші результати. (Правильні відповіді на слайді).

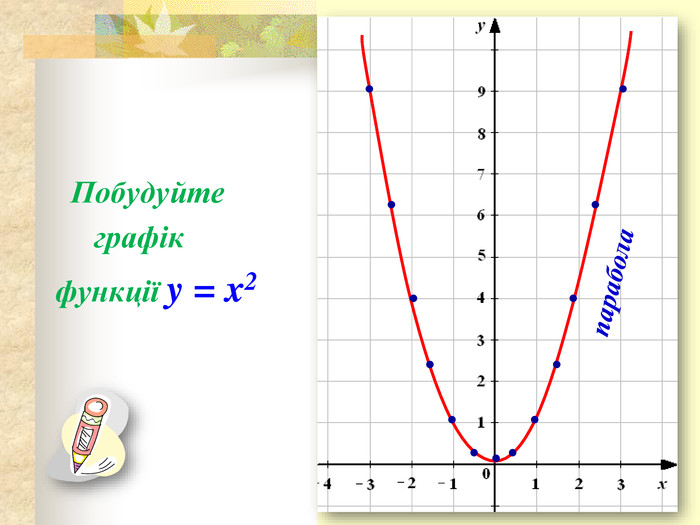
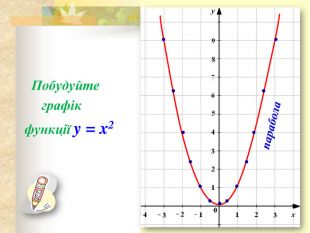
    ●  Побудуємо  графік функції.

  За даними таблицями учнями будують графік функцій, учитель надає необхідну допомогу  дітям, що потребують додаткової педагогічної уваги.

    ● Розглянемо, що ж ми отримали? 

 

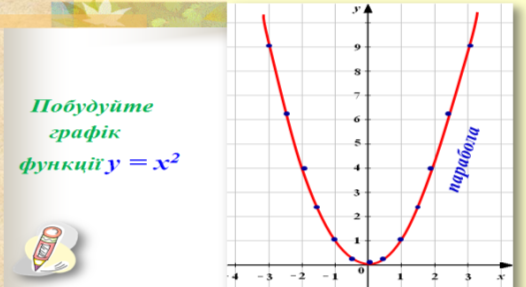
    ● Так, ми побудували криву, яка є графіком функції у = х². Зрозуміло, що цей графік необмежено продовжується вверх, справа і зліва від осі у. Зверніть увагу на вид графіка біля початку координат. Для значень х, близьких до нуля, графік практично зливається з прямою Ох. У такій ситуації говорять, що крива дотикається  до  осі абсцис.

    ● Графік цієї  функції  називають параболою. 

Звідки ж взялась  назва – «парабола», що вона означає? Щоб зрозуміти відповіді на ці питання  розглянемо наступний слайд.

     Древньогрецький математик Аполлоній Пергський за 200 років до нашої ери, розрізавши конус, лінію зрізу назвав параболою, що в перекладі з грецької означає «притча», про що математик і написав у восьмитомнику «Конічні перерізи». І протягом довгого часу параболою назвали тільки лінію перерізу  конуса, поки не з'явилася квадратична функція.

                                          Чи знаєте ви , що

Траєкторія каменю, кинутого під кутом до горизонту, футбольного або баскетбольного м'яча, що летить,  артилерійського снаряду, є параболою (при відсутності опору повітря). Тож все, що ми кинемо під кутом до горизонту, буде летіти  по параболі, оскільки рух під дією гравітації підкоряється законам квадратичної функції.

Струмені води фонтана також описують траєкторію у вигляді параболи.

Форму параболи приймають орбіти комет, супутників та космічних кораблів.

Парабола володіє оптичними  властивостями: всі промені, що виходять із джерела світла, що знаходиться в фокусі параболі (певна точка), відображені паралельно її осі. Ця властивість параболи використовується при виготовленні прожекторів, автомобільних фар, кишенькових ліхтариків, а також параболічних антен.

●  Параболу можна зустріти і в природі.

 

● Продовжимо дослідження. Наше завдання -  з'ясувати, якими властивостями володіє функція у = х² і як ці властивості відображуються на її графіці. Для цього виконайте  завдання №4.

Опираючись на таблицю значень та графік функції, учні заповнюють таблицю в бланку дослідження, отримуючи при цьому  властивості функції  та відображення цих властивостей на графіку. Учитель контролює роботу та надає необхідну допомогу.

  ● Обговоримо  властивості функції у = х². Учні  формулюють властивості, а учитель, з їх допомогою, коментує  і робить необхідні доповнення, використовуючи слайди.

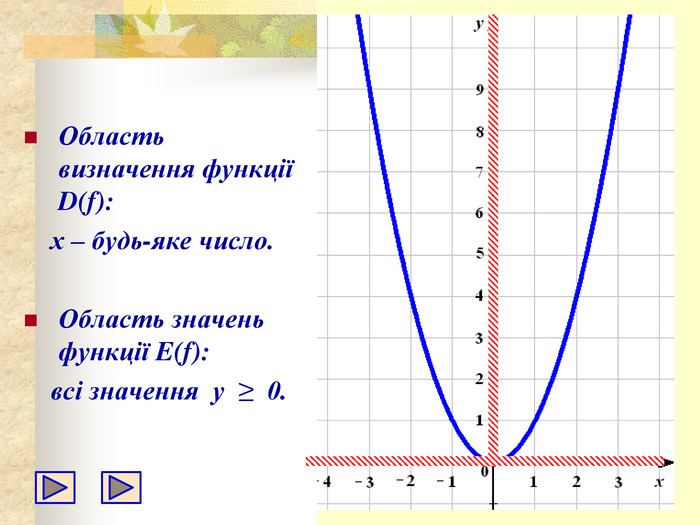
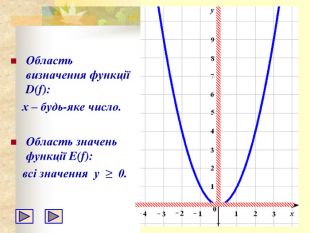
1. Область визначення функції складається з усіх чи­сел.
2. Областю значень функції є множина всіх невід'єм­них чисел: у 0.

 

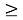
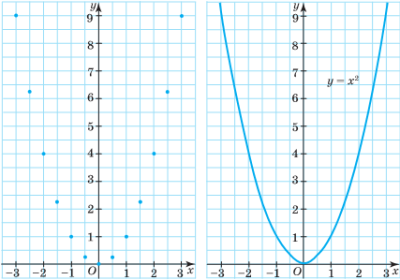
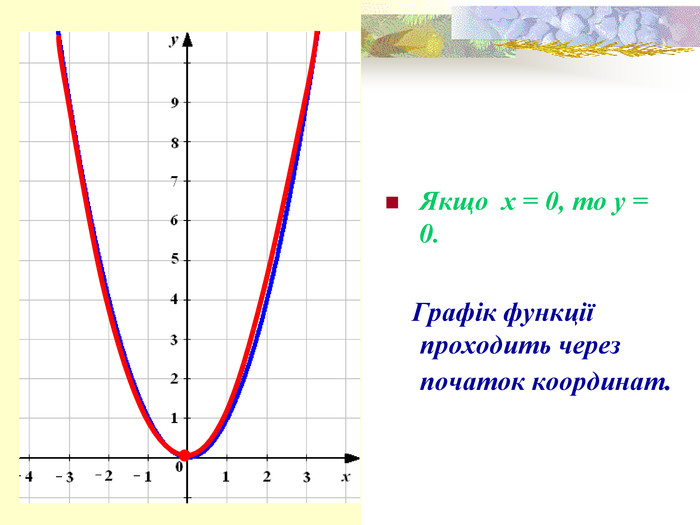
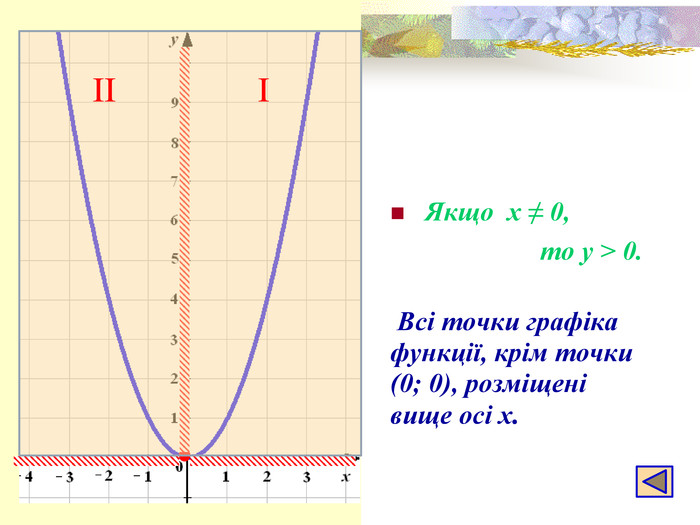
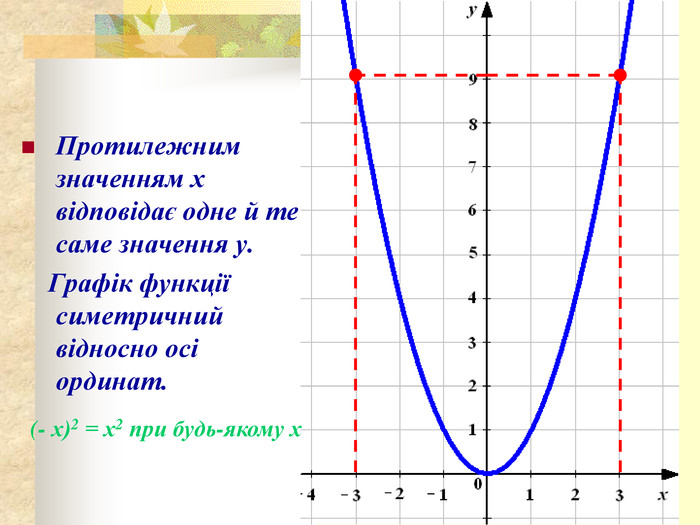
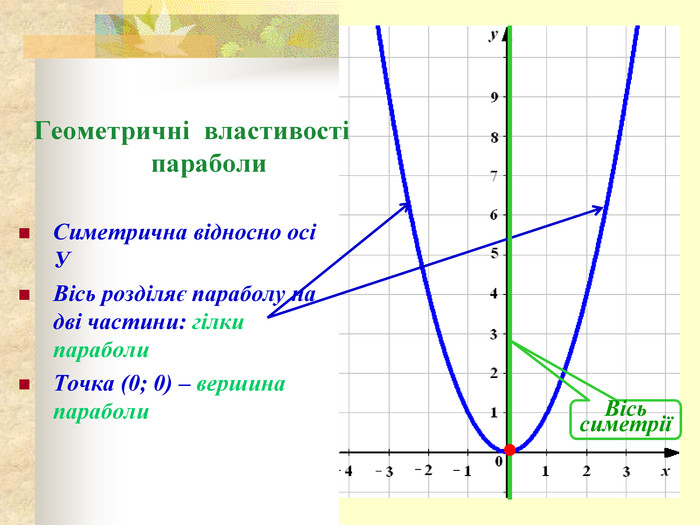
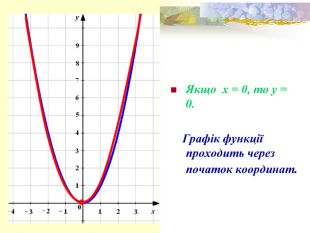
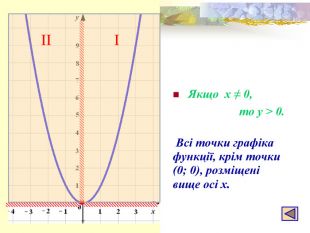
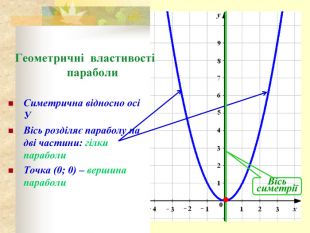
3. Графік функції — парабола, її гілки напрямлені вго­ру, а вершиною є точка  (0; 0). Всі точки графіка, крім вершини параболи, розміщені вище від осі абсцис.
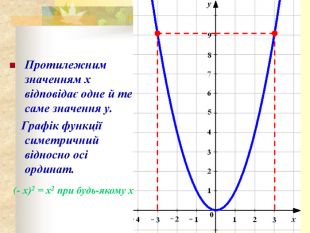
4. Протилежним значенням аргументу відповідає одне й те саме значення функції. Це випливає з того, що 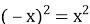при будь-якому значенні .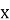

За допомогою графіків функцій можна знайти значення коренів деяких рівнянь, тобто розв’язати  рівняння графічним способом. Розглянемо на прикладі цей спосіб розв’язування рівнянь.

Приклад 1. Розв'язати графічно рівняння  х² = 3-2х.

Розв'язання

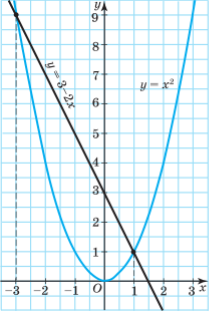Побудуємо графіки функцій у = і у = 3-2х. Графік першої функції —парабола, а другої — пряма, що проходить через точки (0; 3) і (2; -1). Абсциси точок перетину графіків: х = -3 і х = 1.

Перевірка:

 1) х = 3; x² = ( -3)² = 9 і 3-2x = 3-2 (-3) = 9;

2) x= 1 , і 3 - 2х = 3 - 21 = 1.

Отже, х = -3 і х = 1 — корені рівняння x² = 3 - 2х.

Відповідь. х = -3, х = 1.

● Отже, сформулюємо  алгоритм розв’язування  рівнянь графічним способом :

1. Побудувати в одній системі координат графіки функцій, що стоять в лівій  та правій  частинах рівнянь.
2. Знайти абсциси точок перетину графіків. Дані значення і будуть коренями рівняння.
3.  Якщо точок перетину немає, то дане рівняння не має розв’язків.

V.  Осмислення та закріплення нового матеріалу

Для досягнення мети уроку, а саме - розв'язування рівнянь виду у = х² за допомогою графіку, розв’яжемо вправи:

Вправа «Мікрофон»

1. Визначте без обчислення, які з точок не належать графіку функції          у = х²:    А (-1; 1);  B (-2; -4); C (0; 8); D(3; -9); E(1,7; 2,89); F(16; 0). Відповідь поясніть.

Робота біля дошки з коментарем

2.  Для функції у = х² знайдіть значення  у, яке відповідає значенням аргументу х= - 5; - 1; 0; 3; 10.
3. Побудуйте графік функції  у =х² , якщо 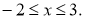  Зверніть увагу на обмеження області визначення функції.

Самостійна робота за варіантами, з подальшим  обговоренням

4. Розв'яжіть графічно рівняння:

 а) (I варіант, 1 учень біля дошки) ;  

 б) (II варіант, 1 учень біля дошки) .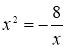

Робота в гетерогенних групах за технологією « Акваріум»

5. Побудуйте графік функції, обґрунтуйте хід міркувань.

       1 група :                                2 група :  

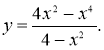
VI. Підсумок уроку  

Наш урок підійшов до завершення. Пропоную повторити навчальний матеріал, який необхідно було засвоїти за допомогою вправи «Незакінчені речення».

Вправа « Незакінчені речення»

1. Залежність, при якій кожному значенню змінної х, ставиться у відповідність єдине значення змінної у називають …
2. Незалежну змінну ще називають …
3. Залежну змінну називають…
4. Усі значення, яких набуває незалежна змінна утворюють …
5. Усі значення, яких набуває залежна змінна утворюють …
6. Область визначення функції  у =х²  складається з …
7. Область значень цієї функції складається  лише з …
8. Графіком функції у =х²  є …
9. Вершина параболи знаходиться у точці, що має координати …
10.  Протилежним значенням аргументу відповідає … значення функції.
11.  Для того, щоб розв’язати рівняння графічним способом необхідно....

VII. Оцінювання навчальних досягнень учнів

VIII. Домашнє завдання

Опрацювати 13, розв’язати:

 № 503, № 507, № 509 – початковий і середній рівні навчальних досягнень;

№ 513, № 515, № 517 – достатній та високий рівні навчальних досягнень.