10 клас, алгебра

Тема уроку.    Похідні  деяких елементарних функцій. Таблиця похідних

Мета уроку: формувати знання учнів про похідну деяких елементарних функцій; вчити знаходити похідні елементарних функцій; розвивати логічне мислення, комунікативність, увагу, пам’ять, здатність до самостійного мислення; виховувати пізнавальну активність, комунікативні навички, мобільність.

Тип уроку:     засвоєння нових знань і вмінь.

Обладнання: мультимедійний проектор, навчальна презентація, дидактичний роздатковий матеріал, смайлики

Очікувані результати:

Після цього уроку учні зможуть:

•            відтворювати таблицю похідних деяких елементарних функцій;
•            застосовувати її під час розв’язування стандартних задач;
• черговий раз переконатися у необхідності та важливості вивчення матеріалу уроку

Хід уроку

1. Організація класу (1хв)

     Рефлексія настрою та готовності до заняття

 Учитель налаштовує учнів на роботу, відмічає відсутніх.

-  Доброго дня, діти! Як настрій? (учні демонструють смайлики з виразом обличчя залежно від їх настрою на початку уроку). Буде можливість на цьому уроці його не зіпсувати, а навіть - покращити. Починаємо!

2. Перевірка домашнього завдання (2 хв)

Один учень (за бажанням) за закритою дошкою виконує с.р., а клас працює на місцях над самостійною роботою на окремих аркушах (вправи дібрано з домашніх номерів, зошити учнів закриті).

Самостійна робота з подальшою самоперевіркою:

1) Користуючись означенням, знайдіть  похідну функції:  f(х)=5-4х,     [ f(х)=3-5х ].

2) Знайдіть значення похідної функції  f(х)=   у точці х =0,2,      [ f( х)=   у точці   х =0,04 ].

3) Знайдіть кутовий коефіцієнт дотичної до графіка функції  у = f(х)  у точці  х , якщо

f (х)=2х+5,    х =-1 ,       [f (х)=3х-1,   х =2  ].

4) Точка рухається за законом s =s(t)  (s вимірюється в метрах). Знайдіть миттєву швидкість точки в момент  t , якщо s (t) =3t +6 t,  t =1 с,            [ s (t) =t +3 t,  t =2 с ].

     Після цього учні звіряються з розв’язанням с.р. учнем, що працював за закритою дошкою, та  здійснюють оцінювання.

(напроти завдань у аркушах ставлять «+» - виконав правильно

«» - частково виконав, «-» - не виконав та здають вчителеві )

3. Актуалізація опорних знань ( 7хв)

Технологія «Мікрофон»

• сформулювати означення похідної;
• механічний зміст похідної;
• геометричний зміст похідної;
• сформулювати правило знаходження похідної;
• який вигляд має рівняння дотичної до графіка функції у заданій точці?

Виконання усних вправ:

1) серед наведених функцій укажіть степеневу: у = х,     у=3х+5,    у =х,    у =х,  у =х+х.

2) подайте у вигляді степеня:  ,    ,    ,     ,     ,     .

3) подайте вираз у вигляді сх, де с – стала величина: ,  ,  ,    -.

4) чому дорівнює f(х), якщо  f(х)=с ( с- стала),    f(х)=х ?

 

4. Мотивація навчальної діяльності учнів, повідомлення теми,  завдань уроку (3 хв)

 Проблемне завдання: Ми вже з вами знаємо як знаходити похідну сталої функції, лінійної, функції, функції арифметичний квадратний корінь.

На ЗНО та наступних уроках, окрім  згаданих функцій, треба вміти знаходити похідні, н-д, таких функцій:

f(х) = х,   f(х)=cоsх,     f(х)=sinx.                  (пригадати назви даних функцій)

Як це зробити? (припущення учнів)

Учитель: Тому тему нашого уроку ви можете спробувати сформулювати самостійно, розгадавши наступний ребус. Пропоную ребус «Тема уроку»

Коник-ліліпут Н=Х				Вівторок, середа

 

							100 м2		Х
									аИа

 

			Я=Й

 

Розгаданий ребус

 

Коник-ліліпут Н=Х				Вівторок, середа
П	О	Х	І	Д	Н	І

 

							100 м2		Х
									аИа
Е	Л	Е	М	Е	Н	Т	А	Р	Н	И	Х

 

Ф	У	Н	К	Ц	І	Й
			Я=Й

 

Учитель: Тема нашого уроку «Похідні  деяких елементарних функцій. Таблиця похідних»

(учні записують у зошитах)

Завдання уроку:

• ознайомитися  з похідними деяких елементарних функцій;
• скласти таблицю похідних елементарних функцій;
•  застосовувативати таблицю похідних елементарних функцій під час розв’язування завдань

Вправа очікування: Що ви очікуєте від нашого сьогоднішнього уроку? Продовжіть речення:

 На уроці ми …

 Я дізнаюся про …

5. Вивчення нового матеріалу та первинне  засвоєння (15 хв)

Перший етап. Похідна степеневої функції

 

 Учитель:  Як знайти похідні функції у = x⁶, у = х²⁰ тощо? Це степеневі функції з цілим показником.

Розглянемо функцію у == хⁿ, де n N. (виконують запис у зошит)

Знайдемо похідну цієї функції, для цього зафіксуємо значення аргументу х. і надамо йому приросту x, тоді:

1) y = (x_o+x)ⁿ - ,

2)

… + .

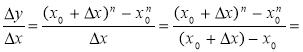
 (Скористалися фор­мулою .

 3) f'(x_o)  + ++…+.

Звідси   (xⁿ)' =nx^{n - 1}, де n  N .

Вчитель Аналогічно знаходиться похідна степеневої функції з цілим від’ємним показником. Зверніть увагу на слайд (запис у зошит не робиться).

На слайді:

Розглянемо функцію y = х^{- n}, де n N.

Знайдемо похідну цієї функції, для цього зафіксуємо значення аргументу х_o і надамо йому приросту Δx, тоді

1) y = (x_o+x)^-n - =,

2) 

.

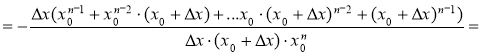
3)

== .

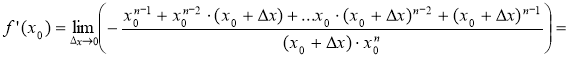
Отже, , де n N.

Висновок: для всіх цілих n виконується рівність: (xⁿ)' = nx^{n – 1}  (учні записують висновок у зошит)

Виконання вправ

1. Знайдіть похідні функції: а) у = х⁶;     б) у = х⁸;     в) y = x²·x⁵;     г) y = .

Відповідь: а) 6х⁵;       б) 8х⁷;      в) 7х⁶;      г) 6х⁵.

2. Знайдіть похідні функцій: а) у = х^-10;  б) y = x²·x^-5;  в) y = ;   г) y = .

Відповідь: а) –10х^-11;  б) -3х^-4;    в) -6х^-7;    г) -6х^-7.

 

Другий етап. Похідні тригонометричних функцій

 

Знайдемо похідну функції у = sin х. Зафіксуємо х_о і надамо аргументу приросту Δх, тоді:

1) Δу = sin(х_о + Δх) - sin х_о

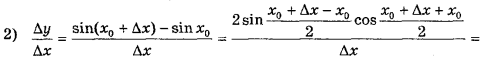
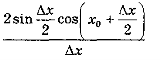
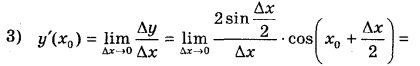
Отже,   (sin х)’ = cos х . Аналогічно можна довести, що  (cos х)' = -sin x  

(можна запропонувати учням довести самостійно або продемонструвати доведення на слайді)

Демонстрація доведення на слайді

(запис у зошит не здійснюється)

На слайді:

 

Знайдемо похідну функції у = tg x. Зафіксуємо х_о і надамо аргументу приросту х, тоді: у = tg(x_о + x) – tg х_о = =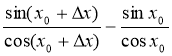

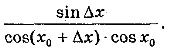
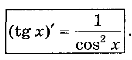
Отже,

 

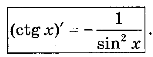
Аналогічно можна довести, що

 

Виконання вправи (з підручника) № 1 с.45 (Нелін Є.П., 11 кл – академічний рівень)

Вчитель: Враховуючи знання, які ви отримали на попередніх уроках та сьогодні, ми можемо заповнити таблицю похідних деяких елементарних функцій.

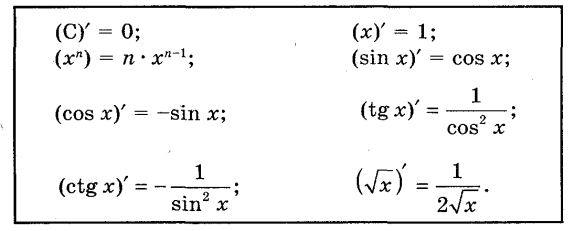
(учні фіксують таблицю у зошиті)

ПОВЕРНЕННЯ ДО ПРОБЛЕМИ: Чи можемо тепер ми знайти похідні функцій f(х) = х,   f(х)=cоsх,     f(х)=sinx ? (так)

Фізкультхвилинка ( 1 хв)

6. Первинне закріплення матеріалу (10 хв)

1. Виконання усних вправ (на пряме застосування формул похідних)

А) Знайдіть похідні функцій:

; ; ; ;

Вчитель: За якою формулою з таблиці знаходили похідну останньої функції? (за похідною степеневої функції)

 

Б) Знайдіть значення похідних функцій:

; ; ; ;

у точках: (якщо це можливо).

2. Виконання вправ за підручником

№ 2 (1, 3), № 11 (2, 4) – колективно

№ 8 (1, 4) – в парах

№ 9 (1, 2) - індивідуально

3. Виконання вправи на повторення

Знайдіть область визначення функції:

1) ;  2) .      

 

7. Підведення підсумків. Рефлексія (3 хв)

Учитель: Що ви сьогодні дізналися на уроці? Чому навчилися?

Відтворіть, чому дорівнює похідна кожної з поданих функцій:

1) , де ; 2) ; 3) ;

4) ; 5) ; 6)  .

Учитель враховує роботу учнів та їх особисте оцінювання під час виконання с.р. на початку уроку, роботи впродовж уроку, оголошує оцінки та коментує їх.

Рефлексія

1. Чи досягли ви очікуваних результатів особисто?
2. Які труднощі особисто у вас виникали на уроці ?
3. Над чим ще необхідно попрацювати?

Підніміть, будь-ласка, смайлики, що демонструють вам теперішній настрій.

8. Домашнє завдання (2 хв) 

Опрацювати теоретичний матеріал § 4  с.41-42 (табл.4)

Виконати за рівнями c.45-46:

С - № 2 (2, 4), № 11 (1, 3), № 3 (1)

Д - № 6 (1, 3), № 9 (3, 4), № 10 (1, 3)

В - № 4, № 7 (1-3), № 16*

Повторити способи розв’язання ірраціональних рівнянь (підручн. 10 кл, § 13 с.205)