Урок дистанційного навчання «Ознака сталості функції. Достатні умови зростання й спадання функції»
Урок дистанційного навчання на платформі Zoom
з алгебри в 10 класі.
Тема уроку: «Ознака сталості функції. Достатні умови зростання й спадання функції».
Мета уроку: познайомити учнів з ознаками сталості функції; дати поняття про достатні умови зростання й спадання функції; сформувати вміння застосовувати ці ознаки до розв’ування задач.
Хід уроку.
І. Організаційний момент. Оголошення теми і мети уроку.
ІІ. Актуалізація опорних знань
Щоб краще опанувати матеріал, дайте відповіді на запитання.
1. Сформулюйте означення функції , що зростає ( спадає ) на проміжку.
2. Опишіть “поведінку“ графіка функції на проміжках її зростання та спадання.
Перевіряємо !
Функція y = f(x) називається зростаючою (спадаючою) на деякому проміжку, якщо для будь-яких x1 і x2, що належать цьому проміжку, із умови x1>x2 слідує, що f(x1)>f(x2 ) (f(x1) < f(x2)).
Сам цей проміжок називається проміжком зростання (спадання) функції.
Приклад:
Зростаюча функція y = 3x+2 .
Спадаючою є функція у =−7x+1.
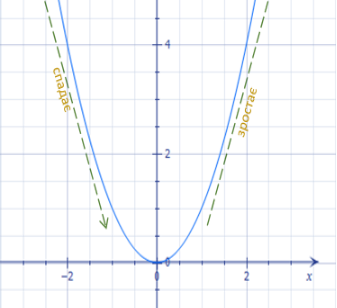
Графік функції y=x2 з показаними проміжками спадання і зростання
Як бачите, за графіком функції досить легко визначати її проміжки зростання та спадання. Для цього достатньо подивитися, від якого значення і до якого по осі Ox графік іде вгору (функція зростає), і між якими значеннями графік прямує вниз (функція спадає). Отриманні значення x слід записати як межі відповідних проміжків.
ІІІ. Вивчення нової теми.
Теорема 1. Якщо у всіх точках відкритого проміжку X виконується нерівність f′(x)≥0 (причому рівність f′(x)=0 виконується лише в окремих точках і не виконується ні на якому суцільному проміжку), тоді функція y=f(x)) зростає на проміжку X.
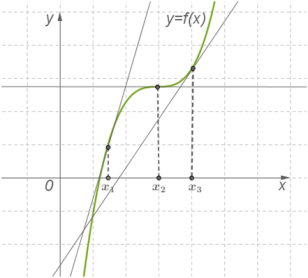
Теорема 2. Якщо у всіх точках відкритого проміжку X виконується нерівність f′(x)≤0 (причому рівність f′(x)=0 виконується лише в окремих точках і не виконується ні на якому суцільному проміжку), тоді функція y=f(x) спадає на проміжкуX.
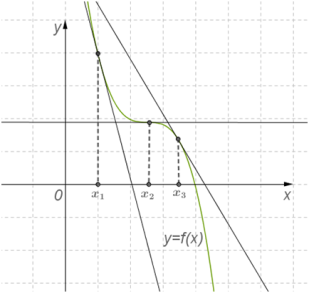
Отже:
якщо існує похідна функції в інтервалі (a,b) і в даному інтервалі
1) f'(x)≥0, тоді функція в ньому не спадає;
2) f'(x)≤0, тоді функція в ньому не зростає;
3) f'(x)>0, тоді функція в ньому зростає;
4) f'(x)<0, тоді функція в ньому спадає.
Приклад:
Необхідно досліджувати інтервали монотонності функції f(x)=x3−4x2−16x+17.
Спочатку знаходимо похідну: f'(x)=(x3−4x2−16x+17)'=3x2−8x−16.
Це парабола, яка перетинає вісь x в точках x1=−43 і x2=4 і її гілки спрямовані вгору. Тому похідна від'ємна в інтервалі (−43;4) (функція спадає) і додатна в інтервалах (−∞;−43) і (4;+∞) (функція зростає).
Відповідь:
функція f(x)=x3−4x2−16x+17 зростає в інтервалах (−∞;−43) і (4;+∞), спадає в інтервалі (−43;4).
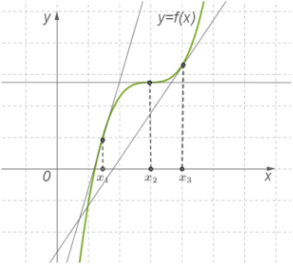
Теорема 2. Якщо у всіх точках відкритого проміжку X виконується нерівність f′(x)≤0 (причому рівність f′(x)=0 виконується лише в окремих точках і не виконується ні на якому суцільному проміжку), тоді функція y=f(x) спадає на проміжкуX.
Отже:
якщо існує похідна функції в інтервалі (a,b) і в даному інтервалі
1) f'(x)≥0, тоді функція в ньому не спадає;
2) f'(x)≤0, тоді функція в ньому не зростає;
3) f'(x)>0, тоді функція в ньому зростає;
4) f'(x)<0, тоді функція в ньому спадає.
Приклад:
Необхідно досліджувати інтервали монотонності функції f(x)=x3−4x2−16x+17.
Спочатку знаходимо похідну: f'(x)=(x3−4x2−16x+17)'=3x2−8x−16.
Це парабола, яка перетинає вісь x в точках x1=−43 і x2=4 і її гілки спрямовані вгору. Тому похідна від'ємна в інтервалі (−43;4) (функція спадає) і додатна в інтервалах (−∞;−43) і (4;+∞) (функція зростає).
Відповідь:
функція f(x)=x3−4x2−16x+17 зростає в інтервалах (−∞;−43) і (4;+∞), спадає в інтервалі (−43;4).
Опорний конспект
Ознака сталості функції
Якщо f ’(x ) = 0 в усіх точках проміжку (а; b), то функція f (x ) стала на цьому проміжку.
Ознаки зростання ( спадання ) функції
Якщо f ’(x ) > 0 при всіх хє(a;b), то функція f (x ) зростає на цьому проміжку.
Якщо f ’(x ) < 0 при всіх хє(a;b), то функція f (x ) спадає на цьому проміжку.
IV. Закріплення вивченого матеріалу.
- Виконання вправи он-лайн в Zoom.
Знайти проміжки зростання та спадання функції у=4х²-16х.
Розв’язання.
у'= 8х −16;
Розв’яжемо нерівності
- 8х −16>0, х>2;
- 8х – 16<0, х<2.
Отже, при Х є [2;+∞) функція зростає, якщо Х є (-∞;2], то функція спадає.
Якщо на кінцях проміжку зростання (спадання) функція неперервна , то їх можна приєднати до цього проміжку.
Відповідь: у ↑, якщо Х є [2;+∞); у ↓, якщо Х є (-∞;2]; 2 - критична точка.
- Розв’яжи завдання самостійно та запиши у зошит. Завдання для самостійної роботи.
№1. Визначте проміжки зростання функції у=х⁴+2х²
|
А |
Б |
В |
Г |
Д |
|
(-∞;-1] |
(-∞;-1] U [0;1] |
[-1;0] |
[-1;0] U [1;+∞) |
інша відповідь |
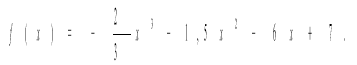
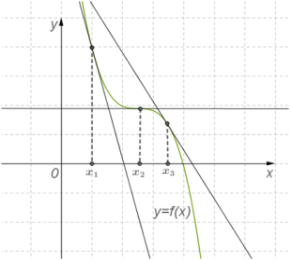
№ 2.Укажіть проміжки спадання функції
|
А |
Б |
В |
Г |
Д |
|
(-∞;+∞) |
(-∞;-⅔] |
[-1;0] |
(-∞;-⅔] U [0;1] |
[-1;0]U[1,5;+∞) |
№ 3. Додаткове завдання.
При яких значеннях а функція  зростає на R?
зростає на R?
V. Домашня робота. Виконати завдання для самостійного опрацювання; вивчити матеріал конспекту.


про публікацію авторської розробки
Додати розробку
