Самостійна робота з теми:"Тригонометричні функції"
Про матеріал
Математика, Мерзляк А.Г., 10 клас, рівень стандарт
33 різних варіанта по 4 завдання
Перегляд файлу
1
Контрольна робота, 10 клас, рівень стандарт
Варіант відповідає порядковому номеру учня в журналі
Зміст
В-1
- Обчисліть: 4 cos450 cos150.
-
Знайдіть
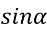 , якщо
, якщо 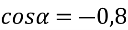 ,
, 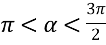 .
.
-
Знайти корінь рівняння
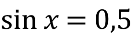
- Розв’яжіть рівняння 3sin2 2x + 10sin2x + 3 = 0
В-2.
- Обчисліть: 4 sin450 sin150.
-
Знайдіть
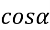 , якщо
, якщо 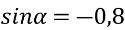 ,
, 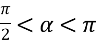 .
.
- Знайти корінь рівняння sin2x=0
- Розв’яжіть рівняння 2cos2 3x − 5cos3x – 3=0
В-3
-
Знайдіть значення виразу -2 cos 60° + sin 30°
 сtg 630°.
сtg 630°.
-
Дано sin = ‑0,6; < <
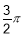 . Обчислити: cos
. Обчислити: cos
-
Знайти корінь рівняння
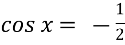 ;
;
- Розв’яжіть рівняння 2 cos2 х – 3 cos х – 2 = 0.
В-4
-
Знайдіть значення виразу 2sin 30° - cos 60°
 tg 225°.
tg 225°.
-
cos = ‑
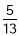 ;
; 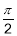 < < . Обчислити: sin
< < . Обчислити: sin
-
Знайти корінь рівняння
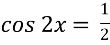
- Розв’яжіть рівняння 2 sin 2 х – 9 sin х – 5 = 0
В-5
-
Обчисліть
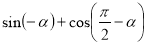
- Знайдіть tg α, якщо соs α = - 0,6 і < α < π.
-
Знайти корінь рівняння
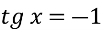
-
Розв’яжіть рівняння
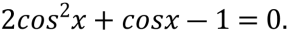
В-6
-
Обчисліть sin (π-α)+ cos (
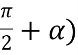
-
Знайдіть значення cosα, якщо відомо, що sinα = -
 і π α
і π α 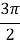 .
.
-
Знайти корінь рівняння
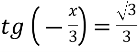
-
Розв’яжіть рівняння
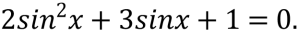
В-7
-
Обчисліть sin (
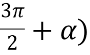 +cos(-α)
+cos(-α)
-
Знайдіть значення cosα, якщо відомо, що sinα =
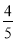 і
і 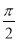 α
α 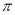 .
.
-

- Розв’яжіть рівняння 2 sin 2 3x − 5 sin 3x – 3=0
В-8
-
Обчисліть cos (π-α)+ sin (
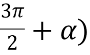
-
Дано sin = ‑0,6; < <
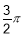 . Обчислити: sin 2
. Обчислити: sin 2
-
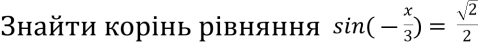
- Розв’яжіть рівняння 3 cos 2 2x + 10 cos 2x + 3 = 0
В-9
-
Обчисліть - cos (
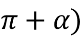 + sin (
+ sin ( +α)
+α)
-
cos = ‑
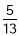 ;
; 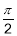 < < . Обчислити: сos 2
< < . Обчислити: сos 2
-
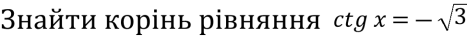
- Розв’яжіть рівняння sinx – 3cos2x = 2.
В-10
-
Спростить вираз (1-sin (
 –
– 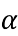 )) (1+sin (
)) (1+sin ( +
+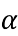 ))
))
- Знайдіть сos 2, якщо tgα = -3
-
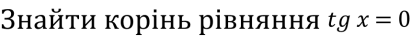
- Розв’яжіть рівняння 2 cos2 х – 5 cos х + 2 = 0.
В-11
-
Обчисліть
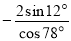
-
cos =
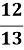 ; 0 < <
; 0 < < 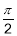 . Обчислити: sin
. Обчислити: sin
-
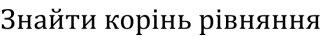
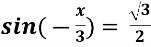
- Розв’яжіть рівняння 6 cos2 х + cos х = 5.
В-12
-
Обчисліть
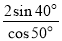
- Знайдіть значення cosα, якщо відомо, що
sinα = - ![]() і π α
і π α ![]()
-
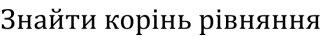
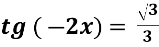
- Розв’яжіть рівняння tg2x + tgx = 2.
В-13
-
Якого найбільшого та найменшого значення може набувати вираз:
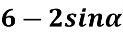
-
Спростіть вираз
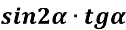
-
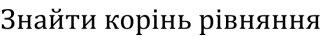
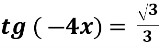
- Розв’яжіть рівняння tg2x - 2tgx – 3 = 0.
В-14
-
Якого найбільшого та найменшого значення може набувати вираз
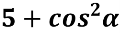
-
Спростіть вираз
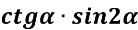
-
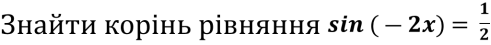
- Розв’яжіть рівняння 4tg2x - tgx – 3 = 0
В-15
-
Якого найбільшого та найменшого значення може набувати вираз
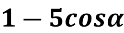
-
Знайдіть значення виразу sin
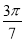 соs
соs  + соз
+ соз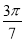 sin
sin  .
.
-
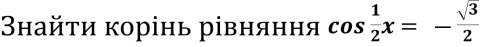
- Розв’яжіть рівняння 2 cos2 х - 3 cos х = -1.
В-16
-
Якого найбільшого та найменшого значення може набувати вираз 4
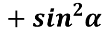 .
.
- Спростіть вираз: sin730 cos170 – cos730 sin(-170).
-
Знайти корінь рівняння
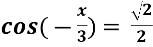
- Розв’яжіть рівняння 3 cos2 х + 5cos х = 2.
В-17
-
Обчисліть
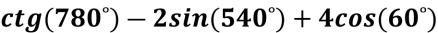
-
Знайдіть значення виразу
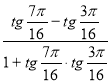 .
.
-
Знайти корінь рівняння
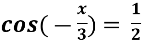
- Розв’яжіть рівняння 2 sin2 х - 3 sin х = -1.
В-18
-
Обчисліть
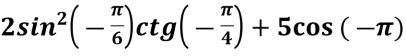
-
Знайдіть значення виразу sіn
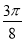 sin
sin 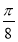 – соs
– соs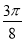 соs
соs 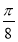 .
.
-
Знайти корінь рівняння
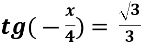
- Розв’яжіть рівняння 2 cos 2 3x − 5 cos 3x – 3=0
В-19
-
Спростіть cos(2700–α) +
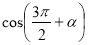 .
.
-
Знайдіть значення виразу соs
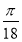 соs
соs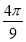 – sin
– sin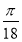 sin
sin 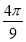 .
.
-
Знайти корінь рівняння
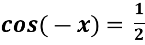
-
Розв’яжіть рівняння 3 cos2
 + 5cos
+ 5cos  = 2.
= 2.
В-20
- Спростити sin 50 ‑ sin 40.
-
Знайдіть sina, якщо соs
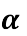 = -
= - 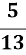 , а
, а 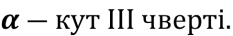
-
Знайти корінь рівняння
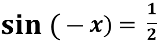
-
Розв’яжіть рівняння 4tg2
 - tg
- tg – 3 = 0
– 3 = 0
В-21
- Спростити sin cos ‑ sin ( + )
-
Спростіть вираз (1 – соs
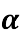 )
) (1 + соs
(1 + соs 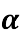 )
)
-
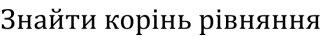
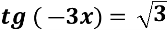
- Розв’яжіть рівняння tg2x + tgx - 2. = 0
В-22
-
Спростити
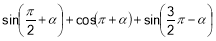
-
Знайдіть tg a, якщо sin
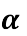 =
=  , а
, а 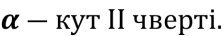
-
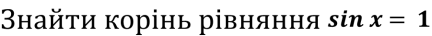
- Розв’яжіть рівняння соs 2x + соs x - 2. = 0
В-23
- Спростити cos 50 ‑ cos 40.
-
Спростіть вираз 1 – sin2
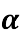 - соs2
- соs2 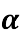
-
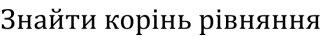
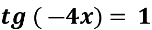
-
Розв’яжіть рівняння 4 sin 2
 - sin
- sin – 3 = 0
– 3 = 0
В-24
- Спростити cos ( ‑ ) ‑ cos cos
-
Спростіть вираз sin2
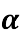 – tg
– tg 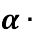 ctg
ctg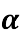 .
.
-
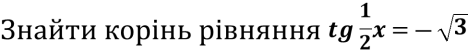
- Розв’яжіть рівняння 6 cos2 2х + cos 2х - 5 = 0.
В-25
-
Спростити
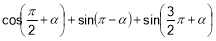
-
Обчисліть вираз
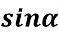 , якщо
, якщо 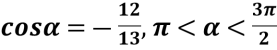 .
.
-
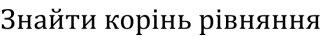 tgx=
tgx=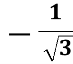
-
Розв’яжіть рівняння
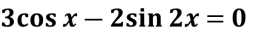
В-26
-
Знайдіть найбільше та найменше значення виразу
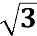 cos α + 8
cos α + 8
-
Дано sin α =
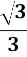 , 90˚< α < 180˚. Знайти cos a.
, 90˚< α < 180˚. Знайти cos a.
-
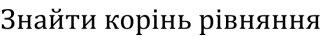 ctg(-x)=
ctg(-x)=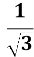
- Розв’яжіть рівняння 6 tg2 2х + tg 2х - 5 = 0
В-27
- Знайдіть найбільше та найменше значення виразу 2 - 3cos α
- Дано cos α = 0,6, 90˚< α < 180˚. Знайти sin α.
-
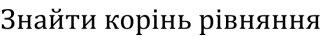 sin (-x)=
sin (-x)=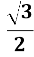
- Розв’яжіть рівняння 3sin2 x + 10sinx + 3 = 0 ;
В-28.
- Знайдіть найбільше та найменше значення виразу 4 - 3cos2 α
-
Дано cos α = -
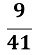 , 90˚< α < 180˚. Знайти sin α.
, 90˚< α < 180˚. Знайти sin α.
-
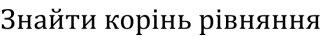 cos (-5x)=
cos (-5x)=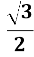
- Розв’яжіть рівняння 2cos2 x − 5cosx = 3.
В-29.
- Знайдіть найбільше та найменше значення виразу 4 – 3sin2 α
- Дано cos α = 0,96; 180˚< α < 270˚. Знайти sin α.
-
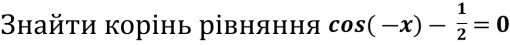
- Розв’яжіть рівняння 2 cos2 (-2x) – 5 cos (-2х) + 2 = 0.
В-30
-
Спростіть sin(1800–α) +
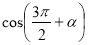 .
.
-
Дано cos α =
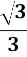 , 90˚< α < 180˚. Знайти sin α
, 90˚< α < 180˚. Знайти sin α
-
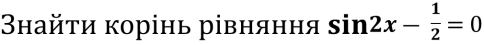
- Розв’яжіть рівняння 2 tg2 (-2x) – 5 tg (-2х) + 2 = 0.
В-31
-
Спростіть cos (π-α)+sin (
 +α)
+α)
-
Дано sin α = -
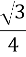 , 180˚< α < 270˚. Знайти cos a.
, 180˚< α < 270˚. Знайти cos a.
-
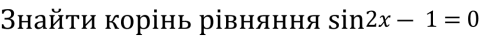
-
Розв’яжіть рівняння
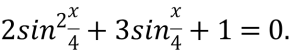
В-32
-
Спростіть sin (π-α) - cos (
 +α)
+α)
-
Спростіть вираз
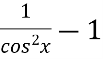
-
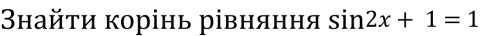
- Розв’яжіть рівняння 2 cos 2 х – 9 cos х – 5 = 0
В -33
- Спростити вираз ctg2α + tg α ctg α
- Спростіть вираз: sin140 cos460 + cos140 sin(-460).
-
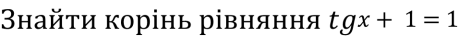
- Розв’яжіть рівняння cos2x-4sinx+4=0.
docx
Оцінка розробки


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку
