Урок в 10 класі "Степенева функція з натуральним показником"
- ~$нспект уроку.docx docx
- Конспект уроку.docx docx
- Презентація.pptx pptx
Слайд1 СТЕПЕНЕВА ФУНКЦІЯ
Доброго дня.
В повсякденному житті нам часто доводиться спостерігати процеси, у яких зміна однієї величини приводить до зміни іншої. Вивчення цих процесів потребує створення їхніх математичних моделей. Однією з таких найважливіших моделей є функція.
На минулих уроках ми з вами повторили означення, основні властивості функції, навчилися досліджувати функції та будувати їх графіки. Сьогодні на уроці ми пригадаємо великий клас функцій, які мають назву степеневі. Усі згадані властивості функцій будуть нам в нагоді для описання властивостей степеневих функцій.
Клик Функції виду ![]() де
де ![]() будь-яке дійсне число, називаються степеневими функціями.
будь-яке дійсне число, називаються степеневими функціями.
Степеневі функції можна поділити на два класи: степенева функція з натуральним показником ![]() де
де ![]() , та степенева функція з цілим показником
, та степенева функція з цілим показником![]() де
де ![]() .
.
Властивості й графіки деяких з них (наприклад, ![]() та
та ![]() ) добре відомі вам з курсу алгебри попередніх класів. Ці функції є окремими випадками степеневої функції.
) добре відомі вам з курсу алгебри попередніх класів. Ці функції є окремими випадками степеневої функції.
Слайд 2
Сьогодні на уроці ми розглянемо степеневу функцію з натуральним показником.
Клик Отже, функції виду ![]() де
де ![]() , називаються степеневими функціями з натуральним показником.
, називаються степеневими функціями з натуральним показником.
Клик Подальше дослідження властивостей степеневої функції з натуральним показником будемо проводити для двох випадків:
-
коли
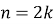 ,
,  , тобто
, тобто 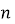 – парне натуральне число
– парне натуральне число
-
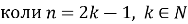 , тобто
, тобто 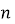 – непарне натуральне число.
– непарне натуральне число.
Слайд 3
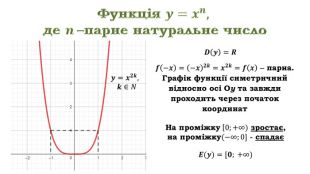
Розглянемо перший випадок. Якщо ![]() парне натуральне число, то функція
парне натуральне число, то функція ![]() де
де ![]() , має властивості і графік, повністю аналогічні властивостям і графіку функції
, має властивості і графік, повністю аналогічні властивостям і графіку функції ![]()
Клик Дійсно, область визначення функції ![]() , оскільки значення цієї функції можна обчислити при будь-яких значеннях
, оскільки значення цієї функції можна обчислити при будь-яких значеннях ![]()
Клик Функція ![]() парна: бо
парна: бо ![]() Отже графік функції
Отже графік функції ![]() симетричний відносно осі Оу.
симетричний відносно осі Оу.
Оскільки при ![]() значення
значення ![]() , то графік функції
, то графік функції ![]() завжди проходить через початок координат.
завжди проходить через початок координат.
Клик На проміжку ![]() функція зростає, а на проміжку
функція зростає, а на проміжку ![]() . З доведенням цих властивостей ви можете ознайомитися самостійно у ваших підручниках
. З доведенням цих властивостей ви можете ознайомитися самостійно у ваших підручниках
Для знаходження області значень функції ![]() складемо рівняння
складемо рівняння ![]() Воно має розв’язки для всіх невід’ємних
Воно має розв’язки для всіх невід’ємних ![]() .
.
Клик Тобто область значень заданої функції ![]() .
.
Клик Враховуючи всі наведені властивості функції ![]() де
де ![]() , одержуємо її графік. За графіком наведеної функції бачимо, що найменше значення функції дорівнює нулю, найбільшого не існує.
, одержуємо її графік. За графіком наведеної функції бачимо, що найменше значення функції дорівнює нулю, найбільшого не існує.
Слайд
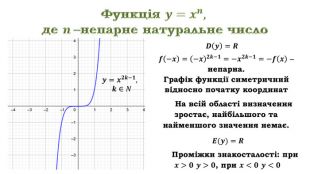
Розглянемо другий випадок, якщо ![]() непарне натуральне число. Нехай
непарне натуральне число. Нехай ![]() . Якщо
. Якщо ![]() парне натуральне число, то графік і властивості функції
парне натуральне число, то графік і властивості функції ![]() аналогічні графіку і властивостям функції
аналогічні графіку і властивостям функції ![]()
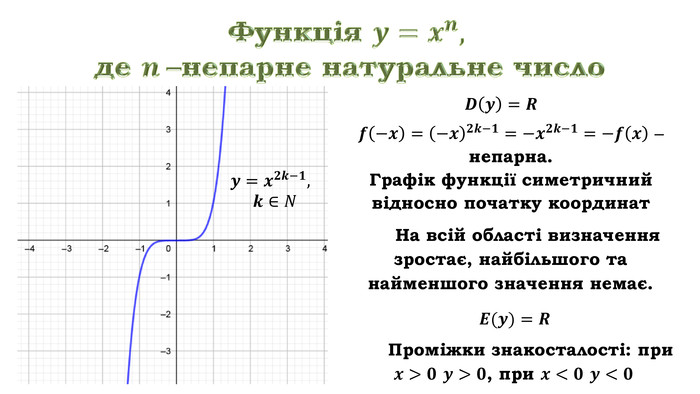
Клик Область визначення степеневої функції з непарним показником – множина всіх дійсних чисел, оскільки значення цієї функції можна обчислити при будь-яких значеннях ![]()
Клик Функція ![]() непарна: бо
непарна: бо ![]() Отже графік функції
Отже графік функції ![]() симетричний відносно початку координат. Оскільки при
симетричний відносно початку координат. Оскільки при ![]() значення
значення ![]() , то графік степеневої функції з непарним показником завжди проходить через початок координат.
, то графік степеневої функції з непарним показником завжди проходить через початок координат.
Клик Дана функція на всій області визначення зростає, найбільшого та найменшого значення немає.
Клик Відповідно область значень даної функції множина всіх дійсних чисел, тобто ![]() .
.
Клик Проміжки знакосталості: при ![]() значення функції додатні, а при
значення функції додатні, а при ![]() - від’ємні.
- від’ємні.
Клик Враховуючи всі наведені властивості функції ![]() одержуємо її графік.
одержуємо її графік.
Хочу зауважити, що графіком функції ![]() є пряма, яка проходить через початок координат, а при всіх інших непарних натуральних
є пряма, яка проходить через початок координат, а при всіх інших непарних натуральних ![]() функція
функція ![]() де
де ![]() , має графік аналогічний графіку функції
, має графік аналогічний графіку функції ![]()
Слайд 5
Узагальнюючи усе вище викладене складемо таблицю властивостей функції ![]() де
де ![]() . Її ви бачити на своїх екранах
. Її ви бачити на своїх екранах
Розв’яжемо декілька прикладів
Слайд 6
Приклад 1. Через які з даних точок проходить графік функції ![]() :
:
1) А (‒1; 1); 2) В (2; 32).
Клик Якщо графік функції проходить через задану точку, то координати цієї точки задовольняють рівнянню даної функції.
Клик Підставимо в рівняння функції ![]() координати точки А: замість х підставимо ‒1, замість у ‒ один. Отримаємо
координати точки А: замість х підставимо ‒1, замість у ‒ один. Отримаємо
![]()
Використовуючи властивості непарного степеня, отримуємо що ![]()
![]()
Отримали невірну числову рівність. Це означає, що точка А (‒1; 1) не належить графіку функції ![]() , тобто Клик графік даної функції не проходить через точку А.
, тобто Клик графік даної функції не проходить через точку А.
Аналогічно перевіряємо точку В (2; 32). Маємо: Клик ![]() ,
, ![]() – отримали вірну числову рівність, тобто Клик графік функції
– отримали вірну числову рівність, тобто Клик графік функції ![]() проходить через точку В.
проходить через точку В.
Слайд Приклад 2 При якому значенні а графік функції ![]() проходить через точку В (‒3; ‒3)
проходить через точку В (‒3; ‒3)
Клик Якщо графік функції проходить через задану точку, то координати цієї точки задовольняють рівнянню даної функції.
Клик Підставимо в рівняння функції координати точки В. Маємо:
Клик ![]()
![]()
![]()
![]() клик: Відповідь:
клик: Відповідь: ![]()
Слайд Приклад 3. Функцію задано формулою ![]() Порівняйте:
Порівняйте:
-
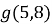 і
і 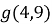 2)
2) 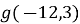 і
і  3)
3) 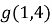 і
і 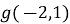
1)![]() і
і ![]()
Для порівняння значень функції в заданих точках скористаємося властивостями степеневої функції. Функцію задано формулою ![]() .
.
Клик Графік степеневої функції з парним натуральним показником на проміжку![]() спадає, а на проміжку
спадає, а на проміжку ![]()
![]() зростає.
зростає.
Клик Значення аргументу ![]() і
і ![]() належать проміжку зростання функції. Відповідно означення зростаючої функції, більшому значенню аргументу відповідає більше значення функції, тобто
належать проміжку зростання функції. Відповідно означення зростаючої функції, більшому значенню аргументу відповідає більше значення функції, тобто
Клик ![]() >
> ![]()
Клик 2) ![]() і
і ![]()
Графік степеневої функції ![]() на проміжку
на проміжку![]() спадає, а на проміжку
спадає, а на проміжку ![]()
![]() зростає. Значення аргументу
зростає. Значення аргументу
Клик ![]() і
і ![]() належать проміжку спадання функції. Відповідно означення спадної функції, більшому значенню аргументу відповідає менше значення функції, тобто
належать проміжку спадання функції. Відповідно означення спадної функції, більшому значенню аргументу відповідає менше значення функції, тобто
Клик ![]() <
< ![]()
Клик 3) ![]() і
і ![]()
Функція ![]() – парна, тобто її графік симетричний відносно осі Оу, тобто значення функції в точках
– парна, тобто її графік симетричний відносно осі Оу, тобто значення функції в точках ![]() . Тоді
. Тоді ![]() . Звідси маємо, що
. Звідси маємо, що
Клик ![]() <
< ![]()
Для порівняння значень степеневої функції з непарним натуральним показником будемо користуватися тільки означенням зростаючої функції, тобто більшому значенню аргументу відповідає більше значення функції.
Слайд 8 Приклад 4 Знайдіть найбільше та найменше значення функції ![]() на проміжку [‒1; 2]
на проміжку [‒1; 2]
Клик Функція ![]() зростає на всій області визначення, тобто більшому значенню аргументу відповідає більше значення функції.
зростає на всій області визначення, тобто більшому значенню аргументу відповідає більше значення функції.
Клик Відповідно найбільшого значення функція набуває в точці х = 2, найменшого ‒ в точці х = ‒1.
Підставимо х = 2 та х = ‒1 у функцію та отримаємо:
Клик ![]() ,
, ![]()
Слайд Приклад 5 Розташуйте в порядку спадання значення виразів

Клик Значення даних виразів запишемо у вигляді функції, тобто ![]() , де
, де ![]() значення виразу, х – основа степеня.
значення виразу, х – основа степеня.
Функція ![]() зростає на всій області визначення, тобто більшому значенню аргументу відповідає більше значення функції.
зростає на всій області визначення, тобто більшому значенню аргументу відповідає більше значення функції.
Порівняємо основи степенів. Для цього зведемо дроби до спільного знаменника 60:
клик ![]() .
.
Враховуючи правило порівняння від’ємних чисел отримаємо:
клик ![]() .
.
Поставивши кожному дробу у відповідність значення степеня запишемо відповідь:
Клик ![]()
Слайд Приклад 6 Розташуйте в порядку зростання значення виразів
![]()
клик Значення даних виразів запишемо у вигляді функції, тобто ![]() , де
, де ![]() значення виразу, х – основа степеня.
значення виразу, х – основа степеня.
клик Функція ![]() парна, тобто значення функції в точках ‒1,06 та 1,06; ‒0,48 і 0,48; ‒2,12 і 2,12; ‒3,25 и 3,25 рівні. Тоді вирази у порядку зростання будуть розташовані наступним чином:
парна, тобто значення функції в точках ‒1,06 та 1,06; ‒0,48 і 0,48; ‒2,12 і 2,12; ‒3,25 и 3,25 рівні. Тоді вирази у порядку зростання будуть розташовані наступним чином:
клик ![]()
Слайд Приклад 7 Знайдіть точки перетину графіків функцій ![]() та
та ![]() .
.
Обидві функції записані у вигляді ![]() . Якщо ліві частині функцій рівні, то праві частини теж рівні. Користуючись цим правилом запишемо:
. Якщо ліві частині функцій рівні, то праві частини теж рівні. Користуючись цим правилом запишемо:
клик ![]() .
.
клик Розв’яжемо отримане рівняння
![]()
![]()
![]() або
або ![]()
![]()
![]()
![]()
Знайдемо значення у, підставивши отримані значення х у будь-яке рівняння функції.
клик ![]()
![]()
![]()
клик Точки перетину графіків функцій (0; 0), (![]() ; 8), (
; 8), (![]()
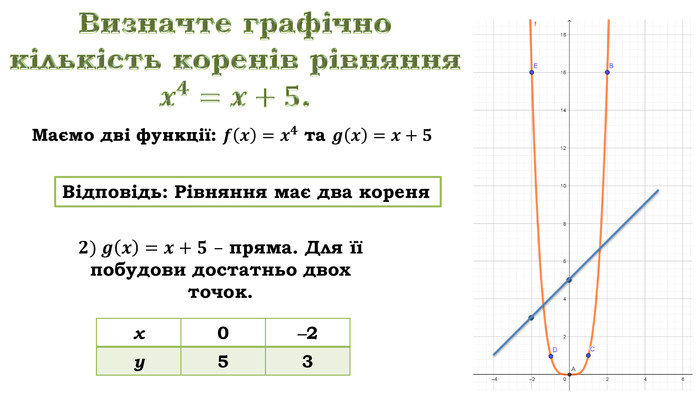
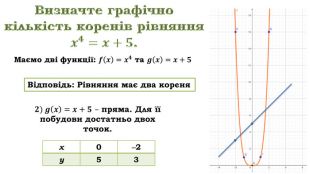
Слайд Приклад 8 Визначте графічно кількість коренів рівняння ![]() .
.
клик У правій та лівій частині даного рівняння стоять функції: ![]() та
та ![]() . Для визначення кількості коренів рівняння
. Для визначення кількості коренів рівняння ![]() побудуємо в одній системі координат графіки обох функцій.
побудуємо в одній системі координат графіки обох функцій.
Опишемо дані функції.
клик 1) ![]() степенева функція з парним показником. Її графік симетричний відносно осі Оу, проходить через початок координат.
степенева функція з парним показником. Її графік симетричний відносно осі Оу, проходить через початок координат.
клик Складемо таблицю значень функції. Виберемо з області визначення декілька значень аргументу, наприклад х = 0, х = 1, х = 2. Підставимо ці значення у функцію та отримаємо точки з координатами (0; 0), (1; 1), (2; 16).
Відмітимо ці точки у системі координат та з’єднаємо їх плавною кривою. Отримали праву частину графіка. Для побудови лівої частини побудуємо точки, симетричні точкам (1; 1), (2; 16) відносно осі Оу і також з’єднаємо їх плавною лінією.
клик Отримали графік функції ![]()
клик 2) ![]()
![]() пряма. Для її побудови достатньо двох точок. Виберемо з області визначення декілька значень аргументу, наприклад х = 0, х = ‒2. Підставимо ці значення у функцію та отримаємо дві точки (0; 5) і (‒2; 3).
пряма. Для її побудови достатньо двох точок. Виберемо з області визначення декілька значень аргументу, наприклад х = 0, х = ‒2. Підставимо ці значення у функцію та отримаємо дві точки (0; 5) і (‒2; 3).
клик Відмітимо ці точки у системі координат та проведемо пряму.
Як бачимо, графіки даних функцій перетинаються у двох точках,
клик тобто рівняння![]() має два кореня
має два кореня
Слайд Приклад 9 Розв’язати рівняння ![]()
Дане завдання відноситься до завдань підвищеного рівня складності. Для розв’язання цього рівняння використовуються властивості спадної (або зростаючої) функції та наступні теореми
Клик
Теорема 1. Якщо функції ![]() та
та ![]() є зростаючими (спадними) на множині М, яка є підмножиною перетину множин
є зростаючими (спадними) на множині М, яка є підмножиною перетину множин ![]() і
і ![]() , то функція
, то функція![]() є зростаючою (спадною) на множині М.
є зростаючою (спадною) на множині М.
Теорема 2. Якщо функція ![]() є зростаючою (спадною), то рівняння
є зростаючою (спадною), то рівняння ![]() де а – деяке число, має не більше одного кореня.
де а – деяке число, має не більше одного кореня.
Слайд Розглянемо дане рівняння.
Клик У його лівій частині стоїть функція ![]() , де
, де ![]() та
та ![]() .
.
Клик Обидві ці функції – степеневі з непарним натуральним показником, тобто зростаючі на всій області визначення.
Клик Відповідно до теореми 1 функція ![]() зростає на всій області визначення.
зростає на всій області визначення.
Клик Тоді рівняння ![]() має не більше одного кореня, який знаходимо методом підбору.
має не більше одного кореня, який знаходимо методом підбору.
Клик Маємо ![]() .
.
Аналогічно розв’язуються рівняння, які містять степені з парним натуральним показником
Сьогодні на уроці ми розглянули степеневі функції з натуральним показником та навчилися використовувати їхні властивості для розв’язування вправ. На наступному уроці ми продовжимо вивчення степеневих функцій, але розглянемо степеневі функції з цілим від’ємним показником. Рекомендую вам повторити властивості степеня з цілим показником. А на сьогодні все. Бажаю вам успіху і до наступної зустрічі


про публікацію авторської розробки
Додати розробку



![Функція 𝒚=𝒙𝒏, де 𝒏 –парне натуральне число 𝒇−𝒙=−𝒙𝟐𝒌=𝒙𝟐𝒌=𝒇𝒙 ‒ парна. Графік функції симетричний відносно осі Оу та завжди проходить через початок координат 1. Область визначення2. Парність 𝑫𝒚=𝑹 3. Проміжки монотонності функціїНа проміжку 0;+∞) зростає, на проміжку(−∞;0] - спадає 4. Область значень 𝑬(𝒚)=[𝟎; +∞) 𝒚=𝒙𝟐𝒌, 𝒌∈𝑁 Функція 𝒚=𝒙𝒏, де 𝒏 –парне натуральне число 𝒇−𝒙=−𝒙𝟐𝒌=𝒙𝟐𝒌=𝒇𝒙 ‒ парна. Графік функції симетричний відносно осі Оу та завжди проходить через початок координат 1. Область визначення2. Парність 𝑫𝒚=𝑹 3. Проміжки монотонності функціїНа проміжку 0;+∞) зростає, на проміжку(−∞;0] - спадає 4. Область значень 𝑬(𝒚)=[𝟎; +∞) 𝒚=𝒙𝟐𝒌, 𝒌∈𝑁](/uploads/files/312761/165165/177822_images/3.jpg)
![{C083 E6 E3-FA7 D-4 D7 B-A595-EF9225 AFEA82}𝑛 – парне натуральне число𝑛 – непарне натуральне число. Область визначення𝑫(𝒚)=𝑹𝑫(𝒚)=𝑹Область значень𝑬(𝒚)=[𝟎; +∞)𝑬𝒚=𝑹Нулі функції𝒙=𝟎𝒙=𝟎 Проміжки знакосталості𝒚>𝟎 на кожному з проміжків −∞;𝟎 та (𝟎; +∞)𝒚>𝟎 на проміжку (𝟎; +∞)𝒚<𝟎 на проміжку −∞;𝟎 Парність. Парна. Непарна. Проміжки монотонностіНа проміжку 𝟎;+∞) зростає, на проміжку (−∞;𝟎]‒спадаєЗростає на всій 𝑫(𝒚){C083 E6 E3-FA7 D-4 D7 B-A595-EF9225 AFEA82}Область визначення. Область значень. Нулі функціїПроміжки знакосталостіПарність. Парна. Непарна. Проміжки монотонностіВластивості функції 𝒚=𝒙𝒏, де 𝑛∈𝑁 {C083 E6 E3-FA7 D-4 D7 B-A595-EF9225 AFEA82}𝑛 – парне натуральне число𝑛 – непарне натуральне число. Область визначення𝑫(𝒚)=𝑹𝑫(𝒚)=𝑹Область значень𝑬(𝒚)=[𝟎; +∞)𝑬𝒚=𝑹Нулі функції𝒙=𝟎𝒙=𝟎 Проміжки знакосталості𝒚>𝟎 на кожному з проміжків −∞;𝟎 та (𝟎; +∞)𝒚>𝟎 на проміжку (𝟎; +∞)𝒚<𝟎 на проміжку −∞;𝟎 Парність. Парна. Непарна. Проміжки монотонностіНа проміжку 𝟎;+∞) зростає, на проміжку (−∞;𝟎]‒спадаєЗростає на всій 𝑫(𝒚){C083 E6 E3-FA7 D-4 D7 B-A595-EF9225 AFEA82}Область визначення. Область значень. Нулі функціїПроміжки знакосталостіПарність. Парна. Непарна. Проміжки монотонностіВластивості функції 𝒚=𝒙𝒏, де 𝑛∈𝑁](/uploads/files/312761/165165/177822_images/5.jpg)


![Функцію задано формулою 𝒈𝒙=𝒙𝟏𝟐. Порівняйте: 𝒙=𝟓,𝟖 і 𝒙=𝟒,𝟗 належать проміжку зростання функції. 𝒈−𝟏𝟐,𝟑 < 𝒈−𝟏𝟓,𝟏 𝟏) 𝒈𝟓,𝟖 і 𝒈𝟒,𝟗 Графік степеневої функції з парним натуральним показником на проміжку (−∞;𝟎]‒ спадає, а на проміжку 𝟎;+∞) ‒ зростає. 𝒈𝟓,𝟖 > 𝒈𝟒,𝟗 𝟐) 𝒈−𝟏𝟐,𝟑 і 𝒈−𝟏𝟓,𝟏 𝒙=−𝟏𝟐,𝟑 і 𝒙=−𝟏𝟓,𝟏 належать проміжку спадання функції. 3) 𝒈𝟏,𝟒 і 𝒈−𝟐,𝟏 Функція 𝒈𝒙=𝒙𝟏𝟐 – парна, тобто 𝒈−𝒙=𝒈𝒙. Тоді 𝒈−𝟐,𝟏=𝒈𝟐,𝟏 𝒈𝟏,𝟒 < 𝒈−𝟐,𝟏 Функцію задано формулою 𝒈𝒙=𝒙𝟏𝟐. Порівняйте: 𝒙=𝟓,𝟖 і 𝒙=𝟒,𝟗 належать проміжку зростання функції. 𝒈−𝟏𝟐,𝟑 < 𝒈−𝟏𝟓,𝟏 𝟏) 𝒈𝟓,𝟖 і 𝒈𝟒,𝟗 Графік степеневої функції з парним натуральним показником на проміжку (−∞;𝟎]‒ спадає, а на проміжку 𝟎;+∞) ‒ зростає. 𝒈𝟓,𝟖 > 𝒈𝟒,𝟗 𝟐) 𝒈−𝟏𝟐,𝟑 і 𝒈−𝟏𝟓,𝟏 𝒙=−𝟏𝟐,𝟑 і 𝒙=−𝟏𝟓,𝟏 належать проміжку спадання функції. 3) 𝒈𝟏,𝟒 і 𝒈−𝟐,𝟏 Функція 𝒈𝒙=𝒙𝟏𝟐 – парна, тобто 𝒈−𝒙=𝒈𝒙. Тоді 𝒈−𝟐,𝟏=𝒈𝟐,𝟏 𝒈𝟏,𝟒 < 𝒈−𝟐,𝟏](/uploads/files/312761/165165/177822_images/8.jpg)
![Знайдіть найбільше та найменше значення функції 𝒚=𝒙𝟕 на проміжку [‒1; 2] 𝒚𝒎𝒂𝒙=𝒚𝟐=𝟐𝟕=𝟏𝟐𝟖 𝒚𝒎𝒊𝒏=𝒚−𝟏=(−𝟏)𝟕=−𝟏 Функція 𝒚=𝒙𝟕 зростає на всій області визначення Відповідно найбільшого значення функція набуває в точці х = 2, найменшого ‒ в точці х = ‒1. Знайдіть найбільше та найменше значення функції 𝒚=𝒙𝟕 на проміжку [‒1; 2] 𝒚𝒎𝒂𝒙=𝒚𝟐=𝟐𝟕=𝟏𝟐𝟖 𝒚𝒎𝒊𝒏=𝒚−𝟏=(−𝟏)𝟕=−𝟏 Функція 𝒚=𝒙𝟕 зростає на всій області визначення Відповідно найбільшого значення функція набуває в точці х = 2, найменшого ‒ в точці х = ‒1.](/uploads/files/312761/165165/177822_images/9.jpg)