Урок алгебри у 8 класі "Квадратні рівняння. Неповні квадратні рівняння"

Тема. Квадратні рівняння. Неповні квадратні рівняння.

Мета: Ввести означення квадратного рівняння, коефіцієнтів квадратного рівняння поняття неповного квадратного рівняння. Ознайомити учнів з методами розв’язування  неповних  квадратних рівнянь Формувати вміння їх розв’язувати. Розвивати пам’ять, логічне мислення, обчислювальні навички. Виховувати критичне мислення та уважність, старанність  та вміння оцінити свої знання.

Тип уроку: урок засвоєння нових знань та формування вмінь та навичок.

Обладнання: макет корабля, опорна схема, таблиця, презентація.

Девіз уроку: «Знати – це означає насамперед уміти користуватися знаннями.»                                                                                                                                         

                                                                                                  В.О.Сухомлинський

Хід уроку

 

І. Організаційний момент.

Сьогодні ми з вами сформуємо команду корабля, щоб відправитись у кругосвітню подорож, якій дамо назву «Квадратні рівняння»

А саме:   капітана, помічники капітана, суднові механіки, електромеханіки, радіоспеціалісти, судновий лікар, боцман.

ІІ. Мотивація навчальної діяльності учнів.

Історична довідка(Розповідає учень): Ще  IV тис. років тому у Стародавньому Вавилоні вміли розв’язувати квадратні рівняння. Пізніше розв’язували їх також у Китаї та Греції. Вивчали  квадратні рівняння такі видатні математики як Евклід і Діофант, Рене Декарт і Нільс Абель, Омар Хайям і Франсуа Вієт.

Особливу увагу квадратним рівнянням приділяв Мухаммед аль-Хорезмі (ІХ ст.). Він показав, як знаходити додатні корені рівнянь.

Індійські вчені у вирішені цього питання пішли далі. Математик

Бхаскара (1114 – 1178), розв’язуючи рівняння знаходив і відֹ’ємні корені,

зауважуючи при цьому, що їх « не слід брати, бо люди не схвалюють від’ємних

абстрактних чисел».

Французького математика Франсуа Вієта називають «батьком» алгебри.

Він першим почав у рівняннях позначати буквами не тільки змінні, а й

коефіцієнти, що дало можливість узагальнити способи розв’язування рівнянь.

Сучасні способи розв’язування квадратних рівнянь поширились

завдяки працям Рене Декарта (1596-1650) та Іссаака Ньютона (1643-1727).

ІІІ. Актуалізація опорних знань.

1.Математичний диктант

1. Рівність, яка містить невідоме називається …
2. Число, яке перетворює рівняння у  правильну рівність називають…
3. Рівняння, що мають однакові корені називають …
4. Розв’язати рівняння означає знайти його розв’язки або…
5. Рівняння виду ах=b, де а і b – довільні числа, х – змінна.
6. Яке лінійне рівняння не має коренів?

Відповіді 1) Рівнянням 2) Коренем рівняння 3) Рівносильні 4) Показати, що їх немає 5)Лінійне рівняння 6) 0х=b, b≠0.                 

2. Усні вправи.

1) Чи є рівносильними рівняння?

а) 4х – 2 = х + 4 і 3х – 6 = 0;

б) 7х – 1 = 5х – х ² і х ² + 2х – 1 = 0;

в) 3х ² – 6х + 15 = 0 і х ² – 2х + 5 = 0.

За  результатами математичного диктанту та усних вправ визначаємо капітана корабля

3. Розв’яжіть рівняння.

а) y – 8 = 0 ; г) 2х - 6= 0;

б) х + 0,3 = 0 ; д) (y - 2) (y +2) = 0 ;

в) 7х = 0 ; е) х ( х – 3 ) = 0.

Після розв’язування рівнянь вибираємо двох помічників капітана

VI. Вивчення нового матеріалу.

З деякими квадратними рівняннями ви вже зустрічались. Наприклад, ви можете розв’язати кожне з рівнянь: х ² = 0, х ² – 4 = 0, х ² + 3х = 0,

та х ² – 4х + 4 = 0. Усі вони мають вигляд ах ² + bх + с = 0.

Означення: Рівняння виду ах ² + bх + с = 0, де х – змінна, а, b, с – числа,

причому а ≠ 0 називається квадратним.

Назва такого рівняння походить від відповідного степеня многочлена лівої  частини рівняння. Число а називають першим (старшим) коефіцієнтом, b – другим   коефіцієнтом, с – вільним членом.

Наприклад: Рівняння 2х ² + 3х – 7 = 0 має такі коефіцієнти: а = 2, b = 3, с = - 7.

Квадратне рівняння, перший коефіцієнт якого дорівнює 1, називається

зведеним. Наприклад: х ² – 2х + 0,5 = 0.

Квадратне рівняння, в якому, хоча б один із коефіцієнтів в або с дорівнює нулю, називають неповним квадратним рівнянням.

Існують три види неповних квадратних рівнянь.

1) при b = с = 0 маємо: ах ² = 0;

2) при с = 0 і b ≠ 0 маємо: ах ² + bх = 0;

3) при b = 0 і с ≠ 0 маємо: ах ² + с = 0.

Розв’яжемо неповне рівняння кожного виду.

1) Рівняння ах ² = 0

х = 0 - єдиний корінь;

2) Рівняння ах ² + bх = 0;

х ( ах + b) = 0;

х = 0 або ах + b = 0;

                ах = - b;

                 х = - b/а.

Має два корені.

3) Рівняння ах ² + с = 0;

ах ² = - с;

х ² = -с/а;

при два корені: х = або х = – ;при - коренів немає.

 

Результати підсумовує така таблиця.

Значення коефіцієнтів b і с	Рівняння	Корені
b = с = 0	ах 2 = 0	х = 0
с = 0,  b ≠ 0	ах 2 + bх = 0	х = 0 або х = - b/а.
b = 0 і с ≠ 0,	ах 2 + с = 0	х = або х = –
b = 0 і с ≠ 0,	ах 2 + с = 0	Коренів немає

 

Зауваження: Квадратне рівняння може мати не більше двох коренів.

Наприклад: ( 3 учні одночасно біля дошки  розв’язують рівняння із слайда презентації   і учні в зошиті)

1) 21х ² = 0;  х ²  = 0;  х = 0.

2) 6х ² – 24х = 0 |:6;

х ² – 4х = 0;

х ( х – 4) = 0;

х = 0 або х – 4 = 0;

                х = 4.

 

 

3) 9х ² – 16 = 0;

(3х) ² – 4 ² = 0;

( 3х – 4)( 3х + 4) = 0;

3х – 4 = 0 або 3х + 4 = 0;

3х = 4;                3х = - 4;

х = ;                     х =

х =х = .

                                                                        ­­­­­­­­­­______               _______

Розв’язавши рівняння, учні стають судновими механіками

 

V. Формування вмінь та навичок.

(На дошці написані вправи на закріплення, робота з підручником О.С.Істер, Алгебра, 8 клас, Київ «Генеза»2016)

№775(усно), 776(усно),777, 778, 784(непарні), 786(1, 5).

Усні вправи

Вправа 775. Які з рівнянь є квадратними

1) х² – 2х+ 3 = 0; 2) х ² – 3х³ = 0; 3) = 0;

4) 7х – х ² = 0; 5) 4х– 5 = 2х+7 ; 6) 1 – 5х ² = 0.

Відповіді: 1),4),6) – квадратні.

Вправа 776. Серед  квадратних рівнянь знайдіть неповні; зведені:

1) 2х² + 3х= 0; 2) х ² +4= 0; 3) 2= 0;

4) 5х ² = 0; 5) 7х ² – 21 = 0 ; 6) х ² – х + = 0.

Відповіді: 1),4),5) –  неповні квадратні рівняння;

2),6) –  зведені квадратні рівняння.

 

Присвоюєм професії: електромеханіки, радіоспеціалісти,

 

 

 

 

Письмові вправи

Вправа 777. Випишіть Коефіцієнти а, b, с квадратного рівняння

(Самостійно, 1 учень(судновий лікар) ззаду дошки)

1) 2х² + 3х – 5 = 0;

а = 2, b = 3, с = – 5.

 2) 3х ² + 9= 0;

а = 3, b = 0, с = 9.

 

 3) = 0;

а = , b = 3, с = 7.

 

4) 3х ² = 0;

а = 3, b = 0, с = 0.

 

 5) 7х – х ²  = 0;

а = – 1 , b = 7, с = 0.

 

6) 2+ 4х – х ² = 0

а = –1, b = 4, с = 2.

 

Вправа 778. Складіть квадратне рівняння за його коефіцієнтами

1. а = 3, b = 5, с =

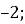
3х² +5х– 2 = 0.

 

2.  а = 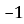 , b = 5, с = 0;

х² + 5х= 0.

 

3. а = 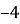, b = 0, с = 0;

            –4х² = 0.

 

4. а =13, b = 0, с =

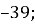
           13х² – 39 = 0.

(Робота в групах)

 

Вправа 784 (непарні). Розв’яжіть рівняння.

1. 3х² – 27= 0;

3х² = 27;

х² = 27 : 3;

          х² =9;

      х =

      Відповідь:

3)2х² + 8 = 0;

2х² = 8;

х² = 8 : 2;

х² = .

Відповідь: коренів немає.

 

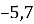5. х² = 0;

              х² = 0;

    х= 0.

        Відповідь:  0.

Вправа 786(1(в групах), 5(біля дошки)) Знайдіть корені рівняння:

1. х² +6х= 0;

х(х+6)=0;

      х =

      ____            х= .

 

Відповідь:   

 

5) х²   = 0   | ∙6;

   2х ²

     х(2х – 1)=0;

х=0  або 2х – 1 = 0;

                2х = 1;

                  х = 0,5.

 

                                                                          Відповідь:

     Після виконання цих вправ старші групи вибирають боцманів, решта матроси.

 

 

 

 

Вправа  на слайді.

При яких значеннях х значення виразу х² – 5х + 7 на 4 більше від значення виразу 2х² + 4х + 3?

х² – 5х + 7 –  4 = 2х² + 4х + 3;

х² – 5х + 3 = 2х² + 4х + 3;

х² – 5х – 2х²  – 4х = 3 – 3;

– х²  – 9х = 0;

х²  + 9х = 0;

х(х+9) = 0;

х=0  або х + 9 = 0;

                х = – 9.

Відповідь:   

 

Ось ми сформували з вами екіпаж корабля , а дальше попливемо з вами у далеке плавання  по темі:  «Квадратні рівняння», яка має таку ж назву як наш корабель.

 

VI. Підбиття підсумків. Оцінювання результатів уроку.

 

VII. Домашнє завдання.

 

Підручник О.С.Істер, Алгебра, 8 клас, Київ «Генеза»2016

Опрацювати § 20 , №№ 783, 785, 787, 790.