Урок алгебри у 9 кл. "Розв’язування квадратних нерівностей графічним способом"
Тема Квадратна нерівність. Розв'язування квадратних нерівностей
Мета уроку: формувати знання учнів про зміст поняття «квадратна
нерівність», домагатися розуміння та засвоєння учнями схеми розв'язування квадратних нерівностей із використанням побудови графіка квадратичної функції, та за готовими графіками квадратичної функції знаходити розв'язки відповідних квадратних нерівностей, а також виконувати послідовні дії відповідно до алгоритму для відшукання розв'язків.
Розвивати мислення, навички реалізації теоретичних знань в
практичній діяльності, інформаційні компетенції, компетенції самоосвіти і саморозвитку.
Виховувати працьовитість, наполегливість,уважність, кмітливість, активність, навички спілкування, групової роботи, позитивне ставлення до навчання.
Очікуванні результати:учні повинні знати означення квадратної нерівності, уміти розв’язувати квадратні нерівності графічним способом.
- вміє працювати з формулами (розуміти змістове значення кожного елемента формули)
- вміє читати і будувати графіки функціональних залежностей, досліджувати їх властивості;
- грамотно висловлюватися рідною мовою; доречно та коректно вживати в мовленні математичну термінологію, чітко, лаконічно та зрозуміло формулювати думку, аргументувати, доводити правильність тверджень; поповнювати свій словниковий запас.
- Тема «Квадратна нерівність. Розв'язування квадратних нерівностей»
Тип уроку: засвоєння нових знань і вмінь.
Наочність та обладнання: комп’ютер, мультимедійний проектор, екран, презентація до уроку, підручник (Алгебра. Підручник для 9 класу. Істер
План уроку
- Організаційний момент.
- Формулювання мети і завдань уроку. Мотивація навчальної
діяльності учнів.
- Актуалізація опорних знань учнів.
- Формування знань.
- Формування вмінь.
- Підсумки уроку.
- Домашнє завдання.
Хід уроку
I. Організаційний момент
Учитель перевіряє готовність учнів до уроку, налаштовує їх на роботу.
II. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів
Учитель зазначає, що учні вже вміють розв’язувати лінійні нерівності та їх системи, і повідомляє, що на цьому уроці вони познайомляться з означенням квадратичної нерівності (або нерівностей другого степеня) та одним із способів розв’язування квадратних нерівностей із використанням побудови графіка квадратичної функції. Мета даного уроку — вивчення означення квадратних нерівностей, схеми їх розв'язування, а також формування вмінь застосовувати вивчене означення та алгоритм для того, щоб знаходити розв'язки квадратних нерівностей.
V. Актуалізація опорних знань та вмінь учнів
Усні вправи
1. (Слайд 2) Серед наведених рівнянь укажіть рівняння, що задають квадратичну функцію:
1) у = 2х2 + х – 1; 2) у2 = х + 1; 3) у2 = х2 – 1;
4) у = -х – х2; 5) у2 = х2; 6) у = -х2.
Для вказаних функцій назвіть коефіцієнти квадратного тричлена (у формулі у = ах2 + bх + с).
Клас працює фронтально. Кожний приклад пояснює новий учень.
2.Що таке квадратична функція? (Слайд 3).
3. Назвати проміжки знакосталості функції, користуючись графіком
(Слайд4). 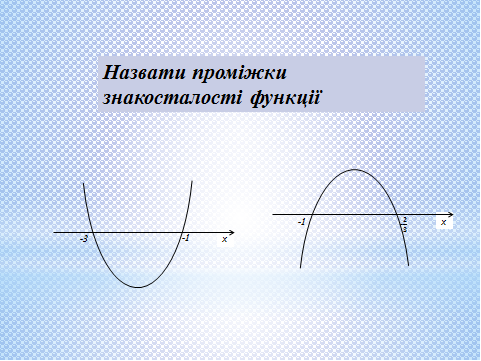
Кожний малюнок пояснює новий учень. Пошук відповіді –
міркування вголос. Клас слідкує за відповіддю товариша, погоджується або висловлює іншу думку.
Учитель підводить підсумки усної роботи. Звертає увагу на допущені помилки, коректує відповіді учнів.
VI. Формування знань
План вивчення нового матеріалу
1. Означення квадратної нерівності. Приклади квадратних нерівностей з різними коефіцієнтами.
2. Схема розв'язування квадратних нерівностей за допомогою побудови графіка відповідної квадратичної функції.
3. Кількість розв’язків квадратної нерівності
1. Означення квадратної нерівності. Приклади квадратних нерівностей з різними коефіцієнтами. (Слайд5).
Виконуючи завдання No2, ми з’ясовували, на яких проміжках функція f(x)=ax2+bx+c набуває додатних значень, а на яких від’ємних.
Встановлюючи проміжки знакосталості функції f(x), ми тим самим
розв’язували нерівності ax2+bx+c >0 і ax2+bx+c<0. Такі нерівності називаються квадратними, якщо а ≠ 0.
(Слайд5) Означення квадратної нерівності, приклади.
Нерівності виду ах2 + bх + с > 0 (<0; ≥ 0; ≤ 0) називаються квадратними, якщо а ≠ 0.
Приклади 3х2 – 2х – 1 > 0, x2 – 9 ≥ 0, х2 – 2х < 0, -х2 > 0
Робота колективна (усно) (слайд №6)
Якщо нерівність має строгий знак (>,<) , то корені квадратного тричлена позначаються «виколотими» точками ( вони виключаються з множини розв’язків нерівності); якщо знак нерівності нестрогий (![]() ) , то корені квадратного тричлена позначаються зафарбованими точками ( вони включаються до множини розв’язків нерівності). Слайд7).
) , то корені квадратного тричлена позначаються зафарбованими точками ( вони включаються до множини розв’язків нерівності). Слайд7).
Давайте подивимось , що може бути розв’язком квадратної нерівності? Слайд8).
2. Схема розв'язування квадратних нерівностей за допомогою побудови графіка відповідної квадратичної функції.
Фронтальна робота.
Розібрати розв’язування нерівності біля дошки х²+4х-5<0
Учням пропонується спробувати вивести алгоритм
розв’язування квадратних нерівностей за допомогою побудови графіка
відповідної квадратної функції.
Після обговорення учні записують у зошити алгоритм розв’язування
квадратних нерівностей графічним способом (Слайд9).
Схема розв'язування квадратних нерівностей 1. Розглянути функцію y=ax2+bx+c.
2. Визначити напрямок віток параболи.
3. Знайти нулі функції (значення x, при яких у=0) або визначити, що їх немає.
4. Побудувати ескіз графіка квадратичної функції у = ах2 + bх + с.
5. За графіком визначити проміжки знакосталості функції та вибрати потрібні.
Для випадку > 0 відповідно отримаємо проміжок (проміжки), для
якого точки параболи лежать вище осі Ох, для випадку < 0 відповідно
отримаємо проміжки (проміжок), для яких точки параболи лежать нижче осі Ох.
- Формування вмінь
Колективне виконання вправ під наглядом учителя.
Робота біля дошки. Приклад №477 з підгучника
Розв’язати нерівність –x2+8x-12≥0
Розв’язання
1. Розглянемо функцію у= –x2+8x-12.
2. Графіком функції
D=82-4·(-1)·(-12) = 64-48=16; D>0,
2. Графіком функції y = –x2+8x-12 є парабола, вітки якої напрямлені вниз,
оскільки a = – 1, –1<0.
3. Ескіз графіка функції
y≥0, якщо [2; 6]
Відповідь: [2; 6]
Усні вправи Знайти розв'язки квадратної нерівності за
готовим графіком відповідної квадратичної функції.
(Слайд №10)
На рисунку зображено графік функції
![]() у= -3х² - 6х.
у= -3х² - 6х.
 Знайдіть множину розв’язків нерівності:
Знайдіть множину розв’язків нерівності:
-
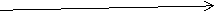 -3х² - 6х < 0; -2 0
-3х² - 6х < 0; -2 0
- -3х² - 6х ≤ 0;
- -3х² - 6х > 0;
-
-3х² - 6х
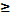 0;
0;
 (Слайд №11)
(Слайд №11)
![]() На рисунку зображено графік функції
На рисунку зображено графік функції
у= х² - 4х +4.
Знайдіть множину розв’язків нерівності:
- х² - 4х +4< 0
-
х² - 4х +4
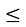 0
0
-
 х² - 4х +4 > 0 2
х² - 4х +4 > 0 2
-

 х² - 4х +4
х² - 4х +4 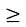 0
0
Письмові вправи.
Розв'язати за вивченою схемою квадратні нерівності
(Слайд №12)
Відповіді для самоперевірки (Слайд №13
З математикою по життю(Слайд №14, 15,16,17)
- Підсумки уроку
(Слайд №18)
1.Який метод розв'язування квадратних нерівностей ви розглянули на уроці?
2. Чому даний метод називають графічним?
3. Графік якої функції потрібно зобразити, щоб знайти розв'язки нерівності?
4. Що є графіком квадратичної функції?
5. Чи потрібно знаходити і позначати координати вершини параболи для схематичного зображення параболи?
6. Які варіанти розміщення віток параболи можливі?
7. Як може бути розміщена парабола відносно осі Ох?
XІ. Домашнє завдання ( Слайд 19)
1. Вивчити означення квадратної нерівності, схему її розв'язування
(§12), повторити теорему про розкладання квадратного тричлена на
лінійні множники (с. 290).
2. Розв'язати вправи N476,482)
Рефлексія (Слайд ). Учням пропонується закінчити речення:
1. На уроці я працював активно / пасивно
2. Своєю роботою на уроці я задоволений / не задоволений
3. Урок мені здався коротким / довгим
4. За урок я не втомився / втомився
5. Матеріал уроку мені був зрозумілим / не зрозумілим
цікавим / не цікавим
6. Домашнє завдання мені здається легким / важким
Заключне слово вчителя.
Виставлення оцінок.
1


про публікацію авторської розробки
Додати розробку
