Урок алгебри в 11 класі: Використання інтеграла для обчислення площ плоских фігур та об'ємів тіл обертання (ділова гра).
Урок алгебри в 11 класі:
Використання інтеграла для обчислення площ плоских фігур та об'ємів тіл обертання.
(ділова гра)
Урок алгебри в 11 класі:
Використання інтеграла для обчислення площ плоских фігур і об'ємів тіл обертання.
(ділова гра)
Мета уроку :
закріплення вмінь учнів користуватися теоретичними знаннями з практики з використанням комп'ютера;
формування умінь учнів використовувати інтеграл для обчислення площ плоских фігур і об'ємів тіл обертання;
напрацювання навичок самоконтролю і самоорієнтації.
Комп'ютерна підтримка: програми GRAN1, GRAN-2D, GRAN-3D.
Хід уроку
I.Вчитель.
Почнемо нашу спільну роботу, з таких слів, які будуть гаслом уроку.
У математиків існує своя мова – мова формул. Розшифруйте математичні записи. Переходячи з однієї кабіни в іншу в чортовому колесі огляду.
Передбачувані відповіді учнів:
Кабіна 1. Операція зворотна диференціюванню називається інтеграцією або відшукуванням первісної, тобто потрібно знайти функцію, знаючи її похідну, іншими словами, знайти перший образ функції.
Кабіна 2. Математичний символ невизначеного інтеграла.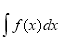 Знайти невизначений інтеграл, це означає знайти усі первісні від нього, при цьому не вказуючи яка саме.
Знайти невизначений інтеграл, це означає знайти усі первісні від нього, при цьому не вказуючи яка саме.
Кабіна 3. Визначений інтеграл 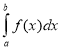 вказує яку саме первісну знайти за допомогою меж інтеграції. Визначений інтеграл - це прирости первісних, тобто різниця первісної.
вказує яку саме первісну знайти за допомогою меж інтеграції. Визначений інтеграл - це прирости первісних, тобто різниця первісної.
Кабіна 4. 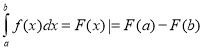
Це формула Ньютона-Лейбніца, за допомогою якої обчислюється площа криволінійної трапеції якщо задана функція буде безперервна на відрізку
Кабіна 5. 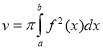
Об'єм будь-якої фігури можна обчислити за допомогою інтеграла, якщо відома формула, якій задана площа фігури.
Вчитель. Чи можна обчислювати первісну, використовуючи табличні інтеграли? – Так, оскільки множина усіх первісних функції називається невизначеним інтегралом. Згадаємо табличні інтеграли за допомогою гри "Простіше простого".
Учні отримують тестові завдання і виконують їх.
Після виконання тестів йде взаємоперевірка і оцінювання робіт учнів.
Приклади тестових завдань.
В - 1
Обчислити інтеграли:
1. ![]() ; а) 1/2; б) 2; в) 1; г) 1,2 .
; а) 1/2; б) 2; в) 1; г) 1,2 .
2. 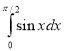 ; а) 0 ; б) 1 ; в) -1 ; г) 2.
; а) 0 ; б) 1 ; в) -1 ; г) 2.
3. 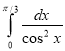 ; а)
; а) ![]() б)
б) ![]() в) -
в) -![]() г)
г) ![]() .
.
4. ![]() ; а) ln2; б) -ln2; в)
; а) ln2; б) -ln2; в) ![]() г) -
г) -![]()
5. ![]() ; а) ln3 ; б) -ln3 ; в)
; а) ln3 ; б) -ln3 ; в) ![]() г) -
г) -![]()
6. 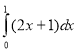 ; a) 1 ; б) 0 ; в) 2 ; г) -1 .
; a) 1 ; б) 0 ; в) 2 ; г) -1 .
В - 2
Обчислити інтеграли:
1. ![]() ; а) 1/2; б) 2; в) 1; г) 1,2 .
; а) 1/2; б) 2; в) 1; г) 1,2 .
2. 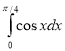 ; а)
; а) ![]() ; б) 1 ; в) -
; б) 1 ; в) - ![]() ; г) 2.
; г) 2.
3. 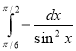 ; а)
; а) ![]() б)
б) ![]() в) -
в) -![]() г)
г) ![]() .
.
4. ![]() ; а) 2; б) -2; в)
; а) 2; б) -2; в) ![]() ; г)
; г) ![]()
5. ![]() ; а) 3 ; б) 2 ; в) -2; г) -3.
; а) 3 ; б) 2 ; в) -2; г) -3.
6. 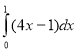 ; a) 1 ; б) 0 ; в) 2 ; г) -1 .
; a) 1 ; б) 0 ; в) 2 ; г) -1 .
II. Формування умінь учнів використовувати інтеграл для обчислення площ плоских фігур і об'ємів тіл обертання.
Вчитель. Згадаємо що таке криволінійна трапеція. Трапеція – це фігура, обмежена графіком безперервної функції y=f(x). Відрізком [a;b] і прямими x=a і x=b.
Трапеція – священна фігура у піфагорійців і можливо в молитвах верховного жерця храму трапеції вам почуються відгомони деяких завдань на побудову. Не бентежтеся, але ж завжди і буває: комусь молитви, а комусь проблеми.
Я книги священною перегортаю сторінки.
Алгоритм, служи зміцненню віри!
Сторін чотирьох вже бачу розміри
І знаю по них побудову відбудеться.
Нехай образ трапеції - нашої богині –
Несе нам щастя і радість віднині.
Обчисливши площі криволінійних трапецій, ви знайдете ключ до розшифровки прізвища того ученого, який сказав:
"Теорія без практики мертва або безплідна:
практика без теорії неможлива або згубна.
Для теорії потрібні знання, для практики, крім того і уміння".
(Декарт)
III. Виконання вправ на ПК із застосуванням програми "GRAN".
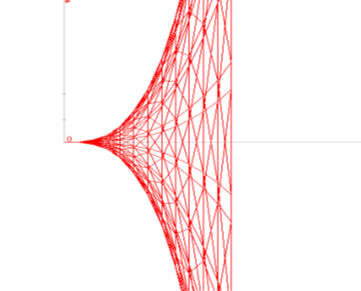
1. Обчислити, заздалегідь побудувавши графіки функцій, площі фігур, обмежених лініями, :
а ) ![]() д)
д) ![]()
б) ![]() е)
е) ![]()
в) ![]()
г) ![]()
Відповіді: а) 2; б) 9; в) 0,4; г) 4,5; д) 4,7; е) 2,7.
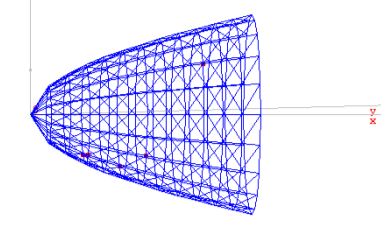
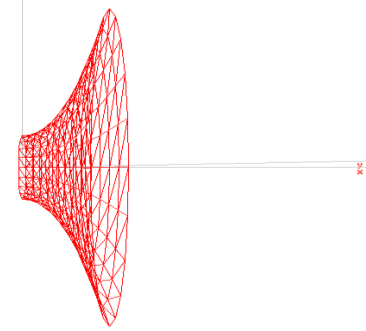
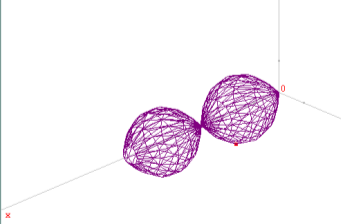
2. Обчислити заздалегідь побудувавши графіки функцій об'єми тіл, утворених при обертанні біля осі абсцис криволінійної трапеції, обмеженої лініями:
|
а) |
|
|
|
б) |
|
|
|
в) |
|
|
|
г) |
|
|
ІV Підведення підсумків уроку.
V Домашнє завдання.
М. І. Шкіль Алгебра і початки аналізу, 11 клас
1


про публікацію авторської розробки
Додати розробку