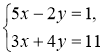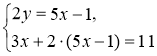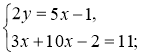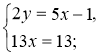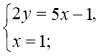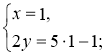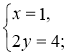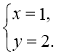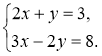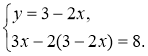Урок алгебри в 7 класі "Повторення. Лінійні рівняння та їх системи"
Урок узагальнення і систематизації знань, вмінь і навичок із розв'язування рівнянь, систем рівнянь та застосування їх до розв'язування задач із використанням частково-пошукового методу, демонстративного методу, бліц-тесту, вправ «Знайди помилку» та «Асоціативний кущ».
Тема. Повторення. Лінійні рівняння та їх системи.
Мета: узагальнити і систематизувати вміння й навички із розв’язування рівнянь, систем рівнянь та застосування їх до розв’язування задач, здійснити проміжну діагностику засвоєння знань та вмінь у ході самостійної роботи;
розвивати пізнавальну активність учнів, інтерес до вивчення теми, логічне мислення;
виховувати інформаційну компетентність, увагу, старанність, культуру математичної мови й запису, впевненості у своїх силах
Тип уроку: узагальнення і систематизації
Обладнання: ПК, мультимедійний проектор, презентація, таблиця, збірники завдань для ДПА з математики для 9 класу, матеріали ЗНО минулих років, картки-завдання, картки самоконтролю
Форми і методи: колективна робота, індивідуальна робота, самостійна робота, частково-пошуковий метод, демонстративний метод, бліц-тест, вправи «Знайди помилку», «Асоціативний кущ».
Перебіг уроку
І. Організаційний момент

І нехай цей урок нашому обдарованому колективу принесе радість та успіх.
ІІ. Перевірка домашнього завдання. Актуалізація опорних знань
- Який матеріал ви повторили вдома?
Три учні працюють біля дошки, розв’язуючи завдання, подібні до домашньої роботи
№1 12х + 3 = х - 8
№2 2(11 – 6х) -3(7 – 4х) = 1
№3 ![]()
Перевірка правильності виконання домашнього завдання на слайдах з коментуванням (СЛАЙД 2) Самоперевірка. Учні отримують 0,5, 1 чи 1,5 бала за кожен правильно розв’язаний номер.

Перевірка розв’язання рівняння учнів біля дошки.
Сьогодні на уроці нам знадобляться ці знання.
- За допомогою бліц-тесту перевіримо як добре ви орієнтуєтесь в рівняннях та їх системах.
▪Бліц-тест (СЛАЙД 3)
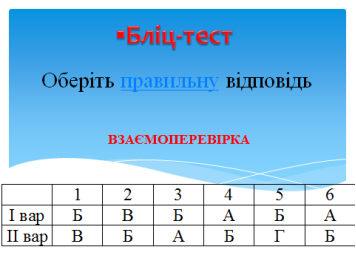
Взаємоперевірка правильності виконання (1 бал за кожну правильну відповідь). (СЛАЙД 3)
|
|
1 |
2 |
3 |
4 |
5 |
6 |
|
І вар |
Б |
В |
Б |
А |
Б |
А |
|
ІІ вар |
В |
Б |
А |
Б |
Г |
Б |
Ті учні, які виконали правильно 3 і більше завдань виконують самостійне розв’язання на вибір (1, 2 або 3 бали):
№56в) 0,7 – 2с = 3с + 1,7 (1 бал)
№64г) 7(у + 6) = 4(3у-5) -3 (2 бали)
№68а) ![]() (3 бали)
(3 бали)
Ті учні, які виконали правильно 1 або 2 завдання ще раз повторюють матеріал теми за Тестовими завданнями (СЛАЙД 4) з коментуванням

- Вкажіть розв'язки рівняння х – у = 2:
1) (3; 2); 2) (3; 1); 3) (5; 2); 4) (-3; -2).
-
Яка з пар є розв'язком системи рівнянь
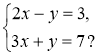
1) (3; 3); 2) (2; 2); 3) (2; 1); 4) (-1; -5). -
Сума двох чисел дорівнює 1, причому одне з них на 5 більше від другого.
Нехай більше число дорівнює х, а менше у. Яка система рівнянь
відповідає умові задачі?
1) 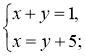 2)
2) 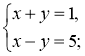 3)
3) 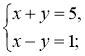 4)
4) 
ІІІ. Оголошення теми і мети уроку. Мотивація
Вправа «Асоціативний кущ» (3 хв) (СЛАЙД 5)

Скажіть, які асоціації викликає у вас словосполучення «застосування рівнянь»? Як ви вважаєте, якою буде тематика сьогоднішнього уроку?
Сьогодні, як ніколи, ми бачимо, що мета нашої роботи не в тому, щоб розв’язати якусь задачу, а в тому, щоб одержати від неї користь.
Фізкультхвилинка.
ІV. Удосконалення знань, умінь та навичок
Найчастіше застосовуємо рівняння до розв’язування систем рівнянь.
№1145б)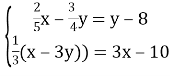
Відповідь: (1,875; 5)
Самостійно виконайте завдання, обираючи за своїм рівнем знань:
№1121а) (1 бал)
Відповідь: (2; 4,5)
№ 1135б) (2 бала)
Відповідь: (10; 2)
№1140а) (3 бала)
Відповідь: (2,04; 5,52)
Самоперевірка з коментуванням за записами на дошці.
На допомогу учню: (роздати картки допомоги слабким учням) ДОДАТОК
Застосування систем рівнянь до розв’язування задач
№207 (збірник Мерзляк). Човен за 3 год руху за течією і 4 год проти течії проходить 114 км. Знайдіть швидкість човна за течією і його швидкість проти течії, якщо за 6 год руху проти течії він проходить такий самий шлях, як за 5 год руху за течією.
![]() Розв’язання. Нехай х км\год швидкість човна, а у км\год швидкість течії. Маємо систему рівнянь: 3(х+у) + 4(х-у) = 114
Розв’язання. Нехай х км\год швидкість човна, а у км\год швидкість течії. Маємо систему рівнянь: 3(х+у) + 4(х-у) = 114
6(х-у) = 5(х+у)
Самостійно виконайте завдання, обираючи за своїм рівнем знань:
№1165 (1 бал)
Відповідь:24 і 11,5
№ 1182 (2 бала)
Відповідь:46см і 38см
№1189 (3 бала)
Відповідь:36 км\год і 4 км\год
Самоперевірка з коментуванням за записами на дошці.
Якщо залишається час:
Задача (збірник «Кенгуру 2011»)
![]() Якщо
Якщо ![]() = 11,
= 11,
![]() = 44, то відношення
= 44, то відношення ![]() дорівнює
дорівнює
А: 2 Б: 3 В: 4 Г: 5 Д: 6
Розв’язання.
![]() 3000 + 5ху = 5. 11у;
3000 + 5ху = 5. 11у;
3000 + 5ху = 5 . 44х. Отже ![]() Відповідь: В
Відповідь: В
V. Підсумок уроку
- Яку тему повторили на уроці?
- Які труднощі залишились?
- Підрахуйте бали, які отримали на уроці.
- Заповніть картки самооцінювання.
|
Картка самооцінювання |
П І учня |
|
Настрій на початку уроку |
|
|
Етапи уроку |
Бали |
|
1. Домашнє завдання (1, 2 або 3 бала) |
|
|
2.Бліц-тест (пройшов поріг так чи ні) |
|
|
3.Розв’язування рівняння (1, 2 або 3 бала) |
|
|
4.Самостійне розв’язання системи (1, 2 або 3 бала) |
|
|
5. Самостійне розв’язання задачі (1, 2 або 3 бала) |
|
|
Сума балів |
|
|
Настрій вкінці уроку (підкресли) |
- все вдалось; -не все вдалось; -було дуже складно; - нічого так і не зрозумів.
|
- Проаналізуйте свою діяльність на уроці. Підніміть руки кому:
- все вдалось;
- не все вдалось, прийдеться вдома подовше посидіти;
- було дуже складно;
- нічого так і не зрозумів.
VІ. Домашнє завдання
Повторити параграфи 24-29,
Виконати: І група №1,6 або ІІ група №5,9 або ІІІ група №7, 10
ДОДАТОК
|
Розв'язування системи лінійних рівнянь із двома змінними способом додавання |
|
|
Приклад |
Коментар |
|
1. |
1. Оскільки жодний з коефіцієнтів змінних не дорівнює ± 1, а коефіцієнти при х пропорційні (кратні), то будемо виражати 2у з першого рівняння: 2у = 5х – 1. |
|
2. |
2. Оскільки 4у = 2 · 2у, то підставимо в друге рівняння замість 2у його вираз через х і дістанемо систему. |
|
3. Відповідь. (1; 2) |
3. Розв'яжемо друге рівняння системи.
4. Знайдемо відповідне значення другої змінної і запишемо відповідь |
|
Розв'язування системи лінійних рівнянь із двома змінними способом підстановки |
|
|
Алгоритм |
Приклад: |
|
1. Виразіть з якого-небудь одного рівняння системи одну змінну через іншу |
1. 3 першого рівняння виразимо через х: у = 3 – 2х |
|
2. Підставте в інше рівняння системи замість цієї змінної здобутий вираз |
2. Підставимо в друге рівняння системи замість у вираз 3 - 2х, дістаємо систему:
|
|
3. Розв'яжіть здобуте рівняння з одним невідомим |
3. Розв'яжемо рівняння: 3х – 2(3 – 2х) = 8; 3х – 6 + 4х = 8; 7х = 14; х = 2 |
|
4. Знайдіть відповідне значення іншої змінної |
4. Знайдемо з рівняння у = 3 - 2х значення у при х = 2: у = 3 – 2 · 2 = -1. Відповідь. (2; -1) |

про публікацію авторської розробки
Додати розробку