Урок "Розв'язування систем лінійних рівнянь з двома змінними графічним способом"

Тема: «Розв'язування систем лінійних рівнянь з двома змінними графічним способом»

Мета:

• навчальна – удосконалити вміння та навички розв’язувати системи лінійних рівнянь з 2-ма змінними графічно; сформувати навички визначати кількість розв’язків системи рівнянь не виконуючи побудову графіків;
• розвивальна – розвивати пам'ять, логічне мислення, увагу, креслярські навички, сконцентрованість;
• виховна – культуру математичних записів, культуру математичного мовлення, інтерес до уроку.

Обладнання: карта подорожі; мультимедійна дошка, роздатковий матеріал.

Хід уроку

I. Організаційний момент.

II. Повідомлення теми і мети уроку.

Урок хочу розпочати словами відомого французького філософа, фізика, математика Рене Декарта : «Недостатньо мати лише гарний розум, головне раціонально його використовувати»

Сьогодні на уроці ми продовжимо вивчати тему «Розв’язування систем лінійних рівнянь з двома змінними графічним способом». Тож розгортаємо зошити, записуємо число , класна робота та тему уроку.  МЕТА. …

Урок проведемо не традиційно: запрошую вас у цікаву подорож по Математичній країні. Я хочу познайомити вас з картою маршруту та правилами подорожі. (карти на партах)

Почнемо подорож з м. Системи рівнянь. Які його координати? (0; 0)

Відвідаємо м. Графіків? Які його координати? (-6; 5)

Також відвідаємо незвичайне м. Нові Знання. Назвіть координати цього міста? (3; 6)

Повернемо до міста Легкої Математики. (6; -3)

І остання наша зупинка м. Королівство таємничих систем.(-5; -4)

Звідси - до Систем рівнянь назад.

Під час подорожі нам траплятимуться різні перешкоди, до яких ми повинні бути готові. Вам доведеться показати свої знання, бути уважними, старанними, не хвилюватися, щоб вчасно повернутися до Систем рівнянь.

III. Розв’язування завдань.

Спочатку перевіримо вашу готовність до такої подорожі.

Для цього перевіримо ваше домашнє завдання. ОБМІНЯЙТЕСЬ ЗОШИТАМИ ВІЗЬМІТЬ ОЛІВЕЦЬ, Я БУДУ КОМЕНТУВАТИ  ПРАВИЛЬНІСТЬ ВИКОНАННЯ завдань.

На ваших партах є кросворд який необхідно розгадати. Отже відповідаємо на запитання.

1. Яка дужка об’єднує рівняння в систему рівнянь? (Фігурна)

2. Що є графіком лінійного рівняння з двома змінними, у якому один з коефіцієнтів відмінний від нуля?(Пряма)

3. Скільки значень змінних входить в розв’язок систем рівнянь. (Пара)

4. Метод розв’язування систем рівнянь, який вивчили (Графічний)

5. Розв’язком системи рівнянь називають спільний розв’язок усіх її … .(Рівнянь)

6. Фігура,що складається з усіх точок площини, координати яких є розв’язками даного рівняння.(Графік)

7. Рівняння,які мають одні і ті самі розв’язки (Рівносильні)

8. Скільки точок достатньо для побудови прямої?(Дві)

І так ми відправляємось з вами у м. Графіків. Щоб подорожувати цим містом, нам слід об’єднатися в групи

1) Розв’язати графічно системи рівнянь:

ЗАВДАННЯ. Розв’яжіть графічно систему:

а)   б) в)

ЩО Є ГРАФІКОМ ЛІНІЙНОГО РІВНЯННЯ З ДВОМА ЗМІННИМИ?

Зробимо висновок: Так як дві прямі на площині можуть перетинатися і мати одну спільну точку або бути паралельними і не мати жодної точки або можуть збігатися тобто мати безліч спільних точок…..так и система може мати один розязок, не мати розвязку або мати безліч розвязків.

Учитель. Як ви гадаєте, чи можна що- небудь сказати про кількість розв’язків системи лінійних рівнянь, не розв’язуючи її? Який є зв’язок між розв’язками системи та коефіцієнтами при невідомих і вільними членами? Запишемо відношення коефіцієнтів, зробимо висновок.

Ми потрапили до м. Нові Знання.

Чи зможете ви дивлячись на дані системи визначити яка кількість розвязків кожної системи?????

ЧКЩО РОЗГЛЯДАТИ СИСТЕМУ ЛІНІЙНИХ РІВНЯНЬ У ЗАГАЛЬНОМУ ВМГЛЯДІ ТО:,…….

 (На мультимедійній дошці висвітлюється перший слайд) ПЕРЕД УЧНЯМИ ОПОРНІ РОЗДРУКОВАНІ КОНСПЕКТИ

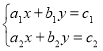 Якщо коефіцієнти біля змінних не пропорційні , то система має єдиний розв’язок.

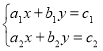  Якщо  коефіцієнти біля змінних і вільні члени  пропорційні, то система має безліч розв’язків.

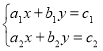   Якщо коефіцієнти біля змінних пропорційні, але не пропорційні вільні члени то система розв’язків

не має.

ФІЗКУЛЬТХВИЛИНКА !!!!

Учитель. А зараз ми вирушаємо до м. Легка Математика. Тут на нас чекає завдання, яке слід відразу виконати.

При якому значенні а система рівнянь

а)   немає розв’язку?

б)   має безліч розв’язків?

Продовжимо подорож. Далі ми слідуємо до м. Королівство таємничих систем.

ЗАВДАННЯ.До рівняння  дібрати інше рівняння, щоб система:

1. мала єдиний розв’язок;
2. мала безліч розв’язків;
3. не мала розв’язку.

Учитель. Ми справились і з цим завданням. А зараз ми повертаємося до м. Системи рівнянь. Подорож наша закінчилася. Але ви розумієте, що Математика - це країна, яка не має меж. На наступному уроці ми з вами вивчатимемо інший спосіб розв’язування систем рівнянь, не менш цікавий.

IV. Підсумок уроку.

1) Скільки розв’язків може мати система двох лінійних рівнянь з двома змінними?

2) У якому випадку система двох лінійних рівнянь з двома змінними має єдиний розв’язок?

3) У якому випадку система двох лінійних рівнянь з двома змінними не має розв’язку?

4) У якому випадку система двох лінійних рівнянь з двома змінними має безліч  розв’язків?

Отож я повернусь до слів Рене Декарта «Недостатньо мати лише гарний розум, головне раціонально його використовувати»

РЕФЛЕКСІЯ

На уроці я:

- дізнався...

- зрозумів...

- навчився...

- найбільший мій успіх - це...

- найбільші труднощі я відчув...

- я не вмів, а тепер умію...

- на наступному уроці я хочу...

-мені сподобалося…

V. Домашнє завдання.